Torus interconnect: Difference between revisions
Anastrophe (talk | contribs) →Disadvantages: we don't use "we". don't write in wikivoice please. |
|||
| (19 intermediate revisions by 14 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Type of geometry for connecting computer nodes}} |
|||
{{cleanup reorganize|date=December 2016}} |
{{cleanup reorganize|date=December 2016}} |
||
A [[torus]] interconnect is a switch-less [[network topology]] for connecting processing nodes in a [[parallel computer]] system. |
A '''[[torus]] interconnect''' is a switch-less [[network topology]] for connecting processing nodes in a [[parallel computer]] system. |
||
[[File:2x2x2torus.svg|thumb|Diagram of a 3-dimensional [[torus]] interconnect. It is not limited to 8 nodes but can consist of any number of nodes in a similar rectilinear array.]] |
[[File:2x2x2torus.svg|thumb|Diagram of a 3-dimensional [[torus]] interconnect. It is not limited to 8 nodes but can consist of any number of nodes in a similar rectilinear array.]] |
||
| Line 8: | Line 9: | ||
=== Geometry illustration === |
=== Geometry illustration === |
||
| ⚫ | In the representations below, the first is a one dimension torus, a simple circle. The second is a two dimension torus, in the shape of a 'doughnut'. The animation illustrates how a two dimension torus is generated from a rectangle by connecting its two pairs of opposite edges. At one dimension, a torus topology is equivalent to a [[Ring network|ring interconnect]] network, in the shape of a circle. At two dimensions, it becomes equivalent to a two dimension mesh, but with extra connection at the edge nodes. |
||
The following images are 1D, and 2D torus. |
|||
| ⚫ | |||
<gallery> |
<gallery> |
||
1d torus circle.png| |
1d torus circle.png|A one dimension torus, a circle. |
||
Toroidal coord.png| |
Toroidal coord.png|A two dimension torus, a donut. |
||
Torus from rectangle.gif| |
Torus from rectangle.gif|Generating a two dimension torus from a two dimension rectangle. |
||
</gallery> |
</gallery> |
||
=== Torus network topology === |
=== Torus network topology === |
||
A torus interconnect is a switch-less topology that can be seen as a [[Mesh networking|mesh interconnect]] with nodes arranged in a [[Rectilinear grid|rectilinear]] array of N = 2, 3, or more dimensions, with processors connected to their [[Nearest neighbor graph|nearest neighbors]], and corresponding processors on opposite edges of the array connected.[[Torus interconnect#cite note-1|[1]]] [[Torus|In this lattice]], each node has 2N connections. This topology is named for the lattice formed in this way, which is topologically homogeneous to an [[N-dimensional]] [[torus]]. |
|||
== Visualization == |
== Visualization == |
||
The first 3 dimensions of torus topology |
The first 3 dimensions of torus network topology are easier to visualize and are described below: |
||
<gallery> |
<gallery> |
||
1d torus.png| |
1d torus.png|1D Torus illustration |
||
2d torus.png| |
2d torus.png|2D Torus illustration |
||
3d torus.png| |
3d torus.png|3D Torus illustration |
||
</gallery> |
</gallery> |
||
*1D Torus: |
*1D Torus: one dimension, ''n'' nodes are connected in closed loop with each node connected to its two nearest neighbors. Communication can take place in two directions, +x and −x. A 1D Torus is the same as [[Ring network|ring interconnection]]. |
||
* 2D Torus: |
* 2D Torus: two dimensions with degree of four, the nodes are imagined laid out in a two-dimensional rectangular lattice of n rows and n columns, with each node connected to its four nearest neighbors, and corresponding nodes on opposite edges connected. Communication can take place in four directions, +x, −x, +y, and −y. The total nodes of a 2D Torus is ''n''<sup>2</sup>. |
||
* 3D Torus: |
* 3D Torus: three dimensions, the nodes are imagined in a three-dimensional lattice in the shape of a rectangular prism, with each node connected with its six neighbors, with corresponding nodes on opposing faces of the array connected. Each edge consists of ''n'' nodes. communication can take place in six directions, +x, −x, +y, −y, +z, −z. Each edge of a 3D Torus consist of n nodes. The total nodes of 3D Torus is ''n''<sup>3</sup>. |
||
* ND Torus: |
* ND Torus: ''N'' dimensions, each node of an ''N'' dimension torus has 2N neighbors, Communication can take place in 2N directions. Each edge consists of n nodes. Total nodes of this torus is ''n''<sup>''N''</sup>. The main motivation of having higher dimension of torus is to achieve higher bandwidth, lower latency, and higher scalability. |
||
Higher-dimensional arrays are difficult to visualize |
Higher-dimensional arrays are difficult to visualize. The above ruleset shows that each higher dimension adds another pair of nearest neighbor connections to each node. |
||
== Performance == |
== Performance == |
||
A number of [[supercomputer]]s on the [[TOP500]] list use three-dimensional torus networks, e.g. IBM's [[Blue Gene#Blue Gene.2FL|Blue Gene/L]] and [[Blue Gene#Blue Gene.2FP|Blue Gene/P]], and the [[Cray]] XT3.<ref name=Torus>N. R. Agida et al. 2005 ''Blue Gene/L Torus Interconnection Network'', IBM Journal of Research and Development, Vol 45, No 2/3 March–May 2005 page 265 {{cite web |url=http://www.cc.gatech.edu/classes/AY2008/cs8803hpc_spring/papers/bgLtorusnetwork.pdf |title=Archived copy |accessdate=2012-02-09 | |
A number of [[supercomputer]]s on the [[TOP500]] list use three-dimensional torus networks, e.g. IBM's [[Blue Gene#Blue Gene.2FL|Blue Gene/L]] and [[Blue Gene#Blue Gene.2FP|Blue Gene/P]], and the [[Cray]] XT3.<ref name=Torus>N. R. Agida et al. 2005 ''Blue Gene/L Torus Interconnection Network'', IBM Journal of Research and Development, Vol 45, No 2/3 March–May 2005 page 265 {{cite web |url=http://www.cc.gatech.edu/classes/AY2008/cs8803hpc_spring/papers/bgLtorusnetwork.pdf |title=Archived copy |accessdate=2012-02-09 |url-status=dead |archiveurl=https://web.archive.org/web/20110815102821/http://www.cc.gatech.edu/classes/AY2008/cs8803hpc_spring/papers/bgLtorusnetwork.pdf |archivedate=2011-08-15 }}</ref> IBM's [[Blue Gene#Blue Gene.2FQ|Blue Gene/Q]] uses a five-dimensional torus network. |
||
Fujitsu's [[K computer]] and the [[PRIMEHPC FX10]] use a proprietary three-dimensional torus 3D mesh interconnect called Tofu.<ref name=postK >''Fujitsu Unveils Post-K Supercomputer'' [http://www.hpcwire.com/hpcwire/2011-11-07/fujitsu_unveils_post-k_supercomputer.html HPC Wire Nov 7 2011]</ref> |
Fujitsu's [[K computer]] and the [[PRIMEHPC FX10]] use a proprietary three-dimensional torus 3D mesh interconnect called Tofu.<ref name=postK >''Fujitsu Unveils Post-K Supercomputer'' [http://www.hpcwire.com/hpcwire/2011-11-07/fujitsu_unveils_post-k_supercomputer.html HPC Wire Nov 7 2011]</ref> |
||
=== 3D Torus performance simulation === |
=== 3D Torus performance simulation === |
||
Sandeep Palur and Dr. Ioan Raicu from Illinois Institute of Technology conducted experiments to simulate 3D torus performance. Their experiments ran on a computer with 250GB RAM, 48 cores and x86_64 architecture. The simulator they used was ROSS ([[Rensselaer’s Optimistic Simulation System]]). They mainly focused on three aspects |
Sandeep Palur and Dr. Ioan Raicu from Illinois Institute of Technology conducted experiments to simulate 3D torus performance. Their experiments ran on a computer with 250GB RAM, 48 cores and x86_64 architecture. The simulator they used was ROSS ([[Rensselaer’s Optimistic Simulation System]]). They mainly focused on three aspects: |
||
* Varying network size |
|||
* Varying number of servers |
|||
* Varying message size |
|||
They concluded that throughput decreases with the increase of servers and network size. Otherwise, throughput increases with the increase of message size.<ref>{{Cite web|url=http://datasys.cs.iit.edu/reports/2014_GCASR14_paper-torus.pdf|title=Understanding Torus Network Performance through Simulations|last1=Sandeep|first1=Palur|last2=Raicu|first2=Dr. Ioan|date=|website=|publisher=|access-date=28 November 2016}}</ref> |
|||
=== 6D Torus product performance === |
=== 6D Torus product performance === |
||
{{main|Torus fusion}} |
|||
[[Fujitsu]] Limited developed a 6D torus computer model. In their model, 6D torus can achieve 100 GB/s off-chip bandwidth, 12 times higher scalability than 3D torus, and high fault tolerance.<ref>{{Cite web|url=http://www.fujitsu.com/downloads/TC/sc10/interconnect-of-k-computer.pdf|title=The 6D Mesh/Torus Interconnect of K Computer|date=|publisher=Fujitsu|access-date=28 November 2016|last1=Inoue|first1=Tomohiro}}</ref> |
[[Fujitsu]] Limited developed a 6D torus computer model called "Tofu". In their model, a 6D torus can achieve 100 GB/s off-chip bandwidth, 12 times higher scalability than a 3D torus, and high fault tolerance. The model is used in the [[K computer]] and [[Fugaku (supercomputer)|Fugaku]].<ref>{{Cite web|url=http://www.fujitsu.com/downloads/TC/sc10/interconnect-of-k-computer.pdf|title=The 6D Mesh/Torus Interconnect of K Computer|date=|publisher=Fujitsu|access-date=28 November 2016|last1=Inoue|first1=Tomohiro}}</ref> |
||
== Advantages |
== Advantages and disadvantages == |
||
=== Advantages === |
=== Advantages === |
||
; Higher speed, lower latency |
|||
Because of the connection of opposite edges, data have more options to travel from one node to another which greatly increased speed. |
: Because of the connection of opposite edges, data have more options to travel from one node to another which greatly increased speed. |
||
; Better fairness |
|||
In a 4×4 mesh interconnect, the longest distance between nodes is from upper left corner to lower right corner. Each datum takes 6 hops to travel the longest path. But in a 4×4 Torus interconnect, upper left corner can travel to lower right corner with only 2 hops |
: In a 4×4 mesh interconnect, the longest distance between nodes is from upper left corner to lower right corner. Each datum takes 6 hops to travel the longest path. But in a 4×4 Torus interconnect, upper left corner can travel to lower right corner with only 2 hops |
||
; Lower energy consumption |
|||
| ⚫ | |||
| ⚫ | |||
=== Disadvantages === |
=== Disadvantages === |
||
;Complexity of wiring |
|||
Extra wires can make the routing process in the physical design phase more difficult. |
:Extra wires can make the routing process in the physical design phase more difficult. To lay out more wires on chip, it is likely there will be a need to increase the number of metal layers or decrease density on chip, which is more expensive. Otherwise, the wires that connect opposite edges can be much longer than other wires. This inequality of link lengths can cause problems because of [[RC time constant|RC delay]]. |
||
| ⚫ | |||
:While long wrap-around links may be the easiest way to visualize the connection topology, in practice, restrictions on cable lengths often make long wrap-around links impractical. Instead, directly connected nodes—including nodes that the above visualization places on opposite edges of a grid, connected by a long wrap-around link—are physically placed nearly adjacent to each other in a folded torus network.<ref>[http://jhnet.co.uk/projects/figures/small_world_torus "Small-World Torus Topology"].</ref><ref>Pavel Tvrdik. [http://pages.cs.wisc.edu/~tvrdik/6/html/Section6.html#AAAAAEmbeddings%20into%20meshes%20and%20tori "Topics in parallel computing: Embeddings and simulations of INs: Optimal embedding of tori into meshes"].</ref> Every link in the folded torus network is very short—almost as short as the nearest-neighbor links in a simple grid interconnect—and therefore low-latency.<ref>[http://www.eurotech.com/DLA/Products_Eurotech/Aurora/HPC_3D_Torus_Short_Paper.pdf "The 3D Torus architecture and the Eurotech approach"].</ref> |
|||
| ⚫ | |||
While long wrap-around links may be the easiest way to visualize the connection topology, in practice, restrictions on cable lengths often make long wrap-around links impractical. |
|||
Instead, directly connected nodes—including nodes that the above visualization places on opposite edges of a grid, connected by a long wrap-around link—are physically placed nearly adjacent to each other in a folded torus network.<ref> |
|||
[http://jhnet.co.uk/projects/figures/small_world_torus "Small-World Torus Topology"]. |
|||
</ref><ref> |
|||
Pavel Tvrdik. |
|||
[http://pages.cs.wisc.edu/~tvrdik/6/html/Section6.html#AAAAAEmbeddings%20into%20meshes%20and%20tori "Topics in parallel computing: Embeddings and simulations of INs: Optimal embedding of tori into meshes"]. |
|||
</ref> |
|||
Every link in the folded torus network is very short—almost as short as the nearest-neighbor links in a simple grid interconnect—and therefore low-latency.<ref> |
|||
[http://www.eurotech.com/DLA/Products_Eurotech/Aurora/HPC_3D_Torus_Short_Paper.pdf "The 3D Torus architecture and the Eurotech approach"]. |
|||
</ref> |
|||
== See also == |
== See also == |
||
Latest revision as of 05:36, 31 January 2024
This article may be in need of reorganization to comply with Wikipedia's layout guidelines. (December 2016) |
A torus interconnect is a switch-less network topology for connecting processing nodes in a parallel computer system.

Introduction
[edit]In geometry, a torus is created by revolving a circle about an axis coplanar to the circle. While this is a general definition in geometry, the topological properties of this type of shape describes the network topology in its essence.
Geometry illustration
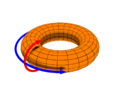
[edit]In the representations below, the first is a one dimension torus, a simple circle. The second is a two dimension torus, in the shape of a 'doughnut'. The animation illustrates how a two dimension torus is generated from a rectangle by connecting its two pairs of opposite edges. At one dimension, a torus topology is equivalent to a ring interconnect network, in the shape of a circle. At two dimensions, it becomes equivalent to a two dimension mesh, but with extra connection at the edge nodes.
-
A one dimension torus, a circle.
-
A two dimension torus, a donut.
-
Generating a two dimension torus from a two dimension rectangle.
Torus network topology
[edit]A torus interconnect is a switch-less topology that can be seen as a mesh interconnect with nodes arranged in a rectilinear array of N = 2, 3, or more dimensions, with processors connected to their nearest neighbors, and corresponding processors on opposite edges of the array connected.[1] In this lattice, each node has 2N connections. This topology is named for the lattice formed in this way, which is topologically homogeneous to an N-dimensional torus.
Visualization
[edit]The first 3 dimensions of torus network topology are easier to visualize and are described below:
-
1D Torus illustration
-
2D Torus illustration
-
3D Torus illustration
- 1D Torus: one dimension, n nodes are connected in closed loop with each node connected to its two nearest neighbors. Communication can take place in two directions, +x and −x. A 1D Torus is the same as ring interconnection.
- 2D Torus: two dimensions with degree of four, the nodes are imagined laid out in a two-dimensional rectangular lattice of n rows and n columns, with each node connected to its four nearest neighbors, and corresponding nodes on opposite edges connected. Communication can take place in four directions, +x, −x, +y, and −y. The total nodes of a 2D Torus is n2.
- 3D Torus: three dimensions, the nodes are imagined in a three-dimensional lattice in the shape of a rectangular prism, with each node connected with its six neighbors, with corresponding nodes on opposing faces of the array connected. Each edge consists of n nodes. communication can take place in six directions, +x, −x, +y, −y, +z, −z. Each edge of a 3D Torus consist of n nodes. The total nodes of 3D Torus is n3.
- ND Torus: N dimensions, each node of an N dimension torus has 2N neighbors, Communication can take place in 2N directions. Each edge consists of n nodes. Total nodes of this torus is nN. The main motivation of having higher dimension of torus is to achieve higher bandwidth, lower latency, and higher scalability.
Higher-dimensional arrays are difficult to visualize. The above ruleset shows that each higher dimension adds another pair of nearest neighbor connections to each node.
Performance
[edit]A number of supercomputers on the TOP500 list use three-dimensional torus networks, e.g. IBM's Blue Gene/L and Blue Gene/P, and the Cray XT3.[1] IBM's Blue Gene/Q uses a five-dimensional torus network. Fujitsu's K computer and the PRIMEHPC FX10 use a proprietary three-dimensional torus 3D mesh interconnect called Tofu.[2]
3D Torus performance simulation
[edit]Sandeep Palur and Dr. Ioan Raicu from Illinois Institute of Technology conducted experiments to simulate 3D torus performance. Their experiments ran on a computer with 250GB RAM, 48 cores and x86_64 architecture. The simulator they used was ROSS (Rensselaer’s Optimistic Simulation System). They mainly focused on three aspects:
- Varying network size
- Varying number of servers
- Varying message size
They concluded that throughput decreases with the increase of servers and network size. Otherwise, throughput increases with the increase of message size.[3]
6D Torus product performance
[edit]Fujitsu Limited developed a 6D torus computer model called "Tofu". In their model, a 6D torus can achieve 100 GB/s off-chip bandwidth, 12 times higher scalability than a 3D torus, and high fault tolerance. The model is used in the K computer and Fugaku.[4]
Advantages and disadvantages
[edit]Advantages
[edit]- Higher speed, lower latency
- Because of the connection of opposite edges, data have more options to travel from one node to another which greatly increased speed.
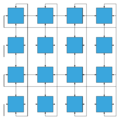
- Better fairness
- In a 4×4 mesh interconnect, the longest distance between nodes is from upper left corner to lower right corner. Each datum takes 6 hops to travel the longest path. But in a 4×4 Torus interconnect, upper left corner can travel to lower right corner with only 2 hops
- Lower energy consumption
- Since data tend to travel fewer hops, the energy consumption tends to be lower.
Disadvantages
[edit]- Complexity of wiring
- Extra wires can make the routing process in the physical design phase more difficult. To lay out more wires on chip, it is likely there will be a need to increase the number of metal layers or decrease density on chip, which is more expensive. Otherwise, the wires that connect opposite edges can be much longer than other wires. This inequality of link lengths can cause problems because of RC delay.
- Cost
- While long wrap-around links may be the easiest way to visualize the connection topology, in practice, restrictions on cable lengths often make long wrap-around links impractical. Instead, directly connected nodes—including nodes that the above visualization places on opposite edges of a grid, connected by a long wrap-around link—are physically placed nearly adjacent to each other in a folded torus network.[5][6] Every link in the folded torus network is very short—almost as short as the nearest-neighbor links in a simple grid interconnect—and therefore low-latency.[7]
See also
[edit]References
[edit]- ^ N. R. Agida et al. 2005 Blue Gene/L Torus Interconnection Network, IBM Journal of Research and Development, Vol 45, No 2/3 March–May 2005 page 265 "Archived copy" (PDF). Archived from the original (PDF) on 2011-08-15. Retrieved 2012-02-09.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Fujitsu Unveils Post-K Supercomputer HPC Wire Nov 7 2011
- ^ Sandeep, Palur; Raicu, Dr. Ioan. "Understanding Torus Network Performance through Simulations" (PDF). Retrieved 28 November 2016.
- ^ Inoue, Tomohiro. "The 6D Mesh/Torus Interconnect of K Computer" (PDF). Fujitsu. Retrieved 28 November 2016.
- ^ "Small-World Torus Topology".
- ^ Pavel Tvrdik. "Topics in parallel computing: Embeddings and simulations of INs: Optimal embedding of tori into meshes".
- ^ "The 3D Torus architecture and the Eurotech approach".