Abbe number

An Abbe diagram plots the Abbe number against refractive index for a range of different glasses (red dots). Glasses are classified using the Schott Glass letter-number code to reflect their composition and position on the diagram.

In physics and optics, the Abbe number, also known as the V-number or constringence of a transparent material, is a measure of the material's dispersion (variation of refractive index with wavelength). It is named for Ernst Abbe (1840–1905), the German physicist who defined it.

The Abbe number V of a material is defined as:

$V={\frac {n_{D}-1}{n_{F}-n_{C}}}$

where n_D, n_F and n_C are the refractive indices of the material at the wavelengths of the Fraunhofer D-, F- and C- spectral lines (589.2 nm, 486.1 nm and 656.3 nm respectively). Low dispersion materials have high values of V.

Abbe numbers are used to classify glasses. For example, flint glasses have V<50 and crown glasses have V >50. Typical values of V range from around 20 for very dense flint glasses, up to 65 for very light crown glass, and up to 85 for fluor-crown glass. Abbe numbers are only a useful measure of dispersion for visible light, and for other wavelengths, or for higher precision work, the group velocity dispersion is used.

Alternate definitions of the Abbe number are used in some contexts. The value V_d is given by:

$V_{d}={\frac {n_{d}-1}{n_{F}-n_{C}}}$

which defines the Abbe number with respect to the yellow Fraunhofer d (or D₃) helium line at 587.5618 nm wavelength. It can also be defined at the green mercury e-line at 546.073 nm:

$V_{e}={\frac {n_{e}-1}{n_{F'}-n_{C'}}}$

where F' and C' are the blue and red cadmium lines at 480.0 nm and 643.8 nm, respectively.

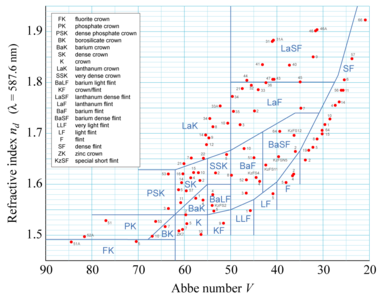
An Abbe diagram is produced by plotting the Abbe number V_d of a material versus its refractive index n_d. Glasses can then be categorised by their composition and position on the diagram. This can be a letter-number code, as used in the Schott Glass catalogue, or a 6-digit glass code.

Abbe numbers are used to calculate the necessary focal lengths of achromatic doublet lenses to minimize chromatic aberration.

See also

• Abbe prism
• Abbe refractometer