Meridian (astronomy): Difference between revisions
m Add citation |
m CheckWiki error #3 and/or general fixes |
||
| Line 5: | Line 5: | ||
In [[astronomy]], the '''meridian''' is the [[great circle]] passing through the [[celestial pole]]s, as well as the [[zenith]] and [[nadir]] of an observer's location. Consequently, it contains also the [[true north|north]] and [[south]] points on the [[horizon]], and it is [[perpendicular]] to the [[celestial equator]] and horizon. Meridians, celestial and geographical, are determined by the [[pencil of planes]] passing through the [[Earth's rotation axis]]. For a location ''not'' at a [[geographical pole]], there is a unique '''meridian plane''' in this axial-pencil through that location. The intersection of this plane with Earth's surface is the ''[[geographical meridian]]'', and the intersection of the plane with the [[celestial sphere]] is the '''celestial meridian''' for that location and time. |
In [[astronomy]], the '''meridian''' is the [[great circle]] passing through the [[celestial pole]]s, as well as the [[zenith]] and [[nadir]] of an observer's location. Consequently, it contains also the [[true north|north]] and [[south]] points on the [[horizon]], and it is [[perpendicular]] to the [[celestial equator]] and horizon. Meridians, celestial and geographical, are determined by the [[pencil of planes]] passing through the [[Earth's rotation axis]]. For a location ''not'' at a [[geographical pole]], there is a unique '''meridian plane''' in this axial-pencil through that location. The intersection of this plane with Earth's surface is the ''[[geographical meridian]]'', and the intersection of the plane with the [[celestial sphere]] is the '''celestial meridian''' for that location and time. |
||
There are several ways to divide the meridian into [[semicircle]]s. In the [[horizontal coordinate system]], the observer's meridian is divided into halves terminated by the horizon's north and south points. The observer's '''upper meridian''', extends from a celestial pole, and passes through the zenith to contact the opposite pole while the '''lower meridian''' passes through the nadir to contact both poles at the opposite ends. Another way, the meridian is divided into the '''local meridian''', the semicircle that contains the observer's zenith and the north and south points of their horizon,<ref>{{Cite web |title=Local Horizon and Meridian |url=https://farside.ph.utexas.edu/books/Syntaxis/Almagest/node15.html |archive-url=https://web.archive.org/web/20240120034733/https://farside.ph.utexas.edu/books/Syntaxis/Almagest/node15.html |archive-date=2024-01-20 |access-date=2024-01-20 |website=farside.ph.utexas.edu}}</ref> |
There are several ways to divide the meridian into [[semicircle]]s. In the [[horizontal coordinate system]], the observer's meridian is divided into halves terminated by the horizon's north and south points. The observer's '''upper meridian''', extends from a celestial pole, and passes through the zenith to contact the opposite pole while the '''lower meridian''' passes through the nadir to contact both poles at the opposite ends. Another way, the meridian is divided into the '''local meridian''', the semicircle that contains the observer's zenith and the north and south points of their horizon,<ref>{{Cite web |title=Local Horizon and Meridian |url=https://farside.ph.utexas.edu/books/Syntaxis/Almagest/node15.html |archive-url=https://web.archive.org/web/20240120034733/https://farside.ph.utexas.edu/books/Syntaxis/Almagest/node15.html |archive-date=2024-01-20 |access-date=2024-01-20 |website=farside.ph.utexas.edu}}</ref><ref>{{Cite web |title=The Local Meridian |url=https://docs.kde.org/trunk5/en/kstars/kstars/ai-meridian.html |access-date=2024-01-21 |website=docs.kde.org}}</ref> and the opposite semicircle, which contains the nadir and the north and south points of their horizon. |
||
On any given (sidereal) day/night, a celestial object will appear to [[diurnal motion|drift across]], or transit, the observer's upper meridian as Earth rotates, since the meridian is fixed to the local horizon. At [[culmination]], the object contacts the upper meridian and reaches its highest point in the sky. An object's [[right ascension]] and the local [[sidereal time]] can be used to determine the time of its culmination (see [[hour angle]]). |
On any given (sidereal) day/night, a celestial object will appear to [[diurnal motion|drift across]], or transit, the observer's upper meridian as Earth rotates, since the meridian is fixed to the local horizon. At [[culmination]], the object contacts the upper meridian and reaches its highest point in the sky. An object's [[right ascension]] and the local [[sidereal time]] can be used to determine the time of its culmination (see [[hour angle]]). |
||
| Line 18: | Line 18: | ||
==References== |
==References== |
||
{{Reflist}} |
|||
*Millar, William (2006). ''The Amateur Astronomer's Introduction to the Celestial Sphere''. Cambridge University Press. |
*Millar, William (2006). ''The Amateur Astronomer's Introduction to the Celestial Sphere''. Cambridge University Press. |
||
*Local Horizon and Meridian. (''A Modern Almagest - An Updated Version of Ptolemy’s Model of the Solar System'' by Richard Fitzpatrick, Professor of Physics, The University of Texas at Austin) |
*Local Horizon and Meridian. (''A Modern Almagest - An Updated Version of Ptolemy’s Model of the Solar System'' by Richard Fitzpatrick, Professor of Physics, The University of Texas at Austin) |
||
{{Authority control}} |
{{Authority control}} |
||
Revision as of 12:16, 21 January 2024
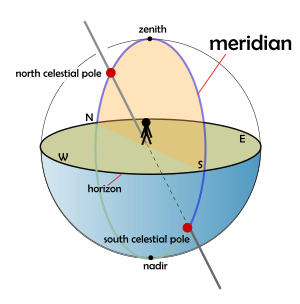
In astronomy, the meridian is the great circle passing through the celestial poles, as well as the zenith and nadir of an observer's location. Consequently, it contains also the north and south points on the horizon, and it is perpendicular to the celestial equator and horizon. Meridians, celestial and geographical, are determined by the pencil of planes passing through the Earth's rotation axis. For a location not at a geographical pole, there is a unique meridian plane in this axial-pencil through that location. The intersection of this plane with Earth's surface is the geographical meridian, and the intersection of the plane with the celestial sphere is the celestial meridian for that location and time.
There are several ways to divide the meridian into semicircles. In the horizontal coordinate system, the observer's meridian is divided into halves terminated by the horizon's north and south points. The observer's upper meridian, extends from a celestial pole, and passes through the zenith to contact the opposite pole while the lower meridian passes through the nadir to contact both poles at the opposite ends. Another way, the meridian is divided into the local meridian, the semicircle that contains the observer's zenith and the north and south points of their horizon,[1][2] and the opposite semicircle, which contains the nadir and the north and south points of their horizon.
On any given (sidereal) day/night, a celestial object will appear to drift across, or transit, the observer's upper meridian as Earth rotates, since the meridian is fixed to the local horizon. At culmination, the object contacts the upper meridian and reaches its highest point in the sky. An object's right ascension and the local sidereal time can be used to determine the time of its culmination (see hour angle).
The term meridian comes from the Latin meridies, which means both "midday" and "south", as the celestial equator appears to tilt southward from the Northern Hemisphere.
See also
- Meridian (geography)
- Prime meridian (planets)
- Prime vertical, the vertical circle perpendicular to a meridian
- Longitude (planets)
References
- ^ "Local Horizon and Meridian". farside.ph.utexas.edu. Archived from the original on 2024-01-20. Retrieved 2024-01-20.
- ^ "The Local Meridian". docs.kde.org. Retrieved 2024-01-21.
- Millar, William (2006). The Amateur Astronomer's Introduction to the Celestial Sphere. Cambridge University Press.
- Local Horizon and Meridian. (A Modern Almagest - An Updated Version of Ptolemy’s Model of the Solar System by Richard Fitzpatrick, Professor of Physics, The University of Texas at Austin)
