Net force: Difference between revisions
Appearance
Content deleted Content added
No edit summary |
No edit summary |
||
| Line 8: | Line 8: | ||
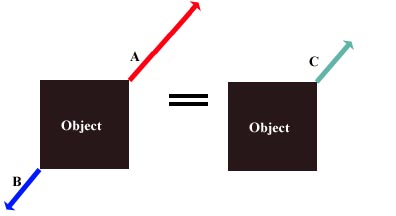
* When force '''A''' and force '''B''' act on an object in opposite directions (180 degrees between then - anti-parallel vectors), the net force ('''C''') is equal to |'''A''' - '''B'''|, in the direction of whichever one has greater [[absolute value]] ("greater magnitude"). |
* When force '''A''' and force '''B''' act on an object in opposite directions (180 degrees between then - anti-parallel vectors), the net force ('''C''') is equal to |'''A''' - '''B'''|, in the direction of whichever one has greater [[absolute value]] ("greater magnitude"). |
||
---- |
---- |
||
[[Image:Non-parallel net force.jpg]] |
[[Image:Non-parallel net force.jpg]] haley coberly is the coolest! |
||
* When the angle between them (the forces) is anything else, then the individual components must be added up using [[sine]] and [[cosine]]. |
* When the angle between them (the forces) is anything else, then the individual components must be added up using [[sine]] and [[cosine]]. |
||
Revision as of 19:45, 23 January 2008
- This article is about forces in physics. For the Luke Van Essen sci-fi novel, see Luke Van Essen's Net Force. For the Tom Clancy novel series see Tom Clancy's Net Force. For the 1999 television movie, see NetForce (film).
- When force A and force B act on an object in the same direction (parallel vectors), the net force (C) is equal to A + B, in the direction that both A and B point. The A point has more force and moves in a separate direction the B will end up not moving to.
- When force A and force B act on an object in opposite directions (180 degrees between then - anti-parallel vectors), the net force (C) is equal to |A - B|, in the direction of whichever one has greater absolute value ("greater magnitude").
File:Non-parallel net force.jpg haley coberly is the coolest!
- When the angle between them (the forces) is anything else, then the individual components must be added up using sine and cosine.
(Note: The illustration assumes that the object, in this case a square, has no center of mass and can be treated like a point.)