Pareto distribution: Difference between revisions
←Blanked the page |
m Reverted edits by 198.36.32.17 to last version by 88.106.223.216 (using Huggle) |
||
| Line 1: | Line 1: | ||
{{Probability distribution| |
|||
name =Pareto| |
|||
type =density| |
|||
pdf_image =[[Image:Pareto_distributionPDF.png|325px|Pareto probability density functions for various ''k'']]<br /><small>Pareto probability density functions for various ''k'' with ''x''<sub>m</sub> = 1. The horizontal axis is the ''x'' parameter. As ''k'' → ∞ the distribution approaches δ(''x'' − ''x''<sub>m</sub>) where δ is the [[Dirac delta function]].</small>| |
|||
cdf_image =[[Image:Pareto_distributionCDF.png|325px|Pareto cumulative distribution functions for various ''k'']]<br /><small>Pareto cumulative distribution functions for various ''k'' with ''x''<sub>m</sub> = 1. The horizontal axis is the ''x'' parameter.</small>| |
|||
parameters =<math>x_\mathrm{m}>0\,</math> [[scale parameter|scale]] ([[real number|real]])<br/><math>k>0\,</math> [[shape parameter|shape]] (real)| |
|||
support =<math>x \in [x_\mathrm{m}; +\infty)\!</math>| |
|||
pdf =<math>\frac{k\,x_\mathrm{m}^k}{x^{k+1}}\!</math>| |
|||
cdf =<math>1-\left(\frac{x_\mathrm{m}}{x}\right)^k\!</math>| |
|||
mean =<math>\frac{k\,x_\mathrm{m}}{k-1}\!</math> for <math>k>1</math>| |
|||
median =<math>x_\mathrm{m} \sqrt[k]{2}</math>| |
|||
mode =<math>x_\mathrm{m}\,</math>| |
|||
variance =<math>\frac{x_\mathrm{m}^2k}{(k-1)^2(k-2)}\!</math> for <math>k>2</math>| |
|||
skewness =<math>\frac{2(1+k)}{k-3}\,\sqrt{\frac{k-2}{k}}\!</math> for <math>k>3</math>| |
|||
kurtosis =<math>\frac{6(k^3+k^2-6k-2)}{k(k-3)(k-4)}\!</math> for <math>k>4</math>| |
|||
entropy =<math>\ln\left(\frac{k}{x_\mathrm{m}}\right) - \frac{1}{k} - 1\!</math>| |
|||
mgf =undefined; ''see text for raw moments''| |
|||
char =<math>k(-ix_\mathrm{m}t)^k\Gamma(-k,-ix_\mathrm{m}t)\,</math>| |
|||
}} |
|||
The '''Pareto distribution''', named after the Italian [[economist]] [[Vilfredo Pareto]], is a [[power law]] [[probability distribution]] that coincides with [[social sciences|social]], [[scientific]], [[geophysical]], [[actuarial science|actuarial]], and many other types of observable phenomena. Outside the field of economics it is at times referred to as the '''[[Bradford's law|Bradford distribution]]'''. |
|||
Pareto originally used this distribution to describe the [[Distribution of wealth|allocation of |
|||
wealth]] among individuals since it seemed to show rather well the way that |
|||
a larger portion of the wealth of any society is owned by a smaller percentage |
|||
of the people in that society. This idea is sometimes expressed more simply as the [[Pareto principle]] or the "[[80-20 rule]]" which says that 20% of the population owns 80% of the wealth<ref>For a two-quantile population, where 18% of the population owns 82% of the wealth, the [[Theil index]] takes the value 1.</ref>. It can be seen from the [[probability density function]] (PDF) graph on the right, that the "probability" or fraction of the population <math>f(x)</math> that owns a small amount of wealth per person (''x'') is rather high, and then decreases steadily as wealth increases. This distribution is not limited to describing wealth or income distribution, but to many situations in which an equilibrium is found in the distribution of the "small" to the "large". The following examples are sometimes seen as approximately Pareto-distributed: |
|||
<!-- THESE TWO SEEM TO BELONG UNDER [[Zipf's law]] RATHER THAN THE PARETO DISTRIBUTION |
|||
* Frequencies of words in longer texts (a few words are used often, lots of words are used infrequently) |
|||
* Frequencies of [[Given_name#Popularity_distribution_of_given_names|given names]] --> |
|||
* The sizes of human settlements (few cities, many hamlets/villages) |
|||
* File size distribution of Internet traffic which uses the TCP protocol (many smaller files, few larger ones) |
|||
* Clusters of [[Bose-Einstein condensate]] near [[absolute zero]] |
|||
* The values of [[oil reserves]] in oil fields (a few large fields, many small fields) |
|||
* The length distribution in jobs assigned supercomputers (a few large ones, many small ones) |
|||
* The standardized price returns on individual stocks |
|||
* Sizes of sand particles |
|||
* Sizes of meteorites |
|||
* Numbers of species per genus (There is subjectivity involved: The tendency to divide a genus into two or more increases with the number of species in it) |
|||
* Areas burnt in forest fires |
|||
* Severity of large [[casualty (person)|casualty]] losses for certain lines of business such as general liability, commercial auto, and workers compensation. |
|||
== Properties == |
|||
=== Definition === |
|||
If ''X'' is a [[random variable]] with a Pareto distribution, then the probability that ''X'' is greater than some number ''x'' is given by |
|||
:<math>\Pr(X>x)=\left(\frac{x}{x_\mathrm{m}}\right)^{-k}</math> |
|||
for all ''x'' ≥ ''x''<sub>m</sub>, where ''x''<sub>m</sub> is the (necessarily positive) minimum possible value of ''X'', and ''k'' is a positive parameter. The family of Pareto distributions is parameterized by two quantities, ''x''<sub>m</sub> and ''k''. When this distribution is used to model the distribution of wealth, then the parameter ''k'' is called the [[Pareto index]]. |
|||
=== Density function === |
|||
It follows that the probability density function is |
|||
:<math>f(x;k,x_\mathrm{m})= k\,\frac{x_\mathrm{m}^k}{x^{k+1}}\ \mbox{for}\ x \ge x_\mathrm{m}. \, </math> |
|||
=== Various properties === |
|||
The [[expected value]] of a [[random variable]] following a Pareto distribution is |
|||
:<math>E(X)=\frac{kx_\mathrm{m}}{k-1} \,</math> |
|||
(if ''k'' ≤ 1, the expected value is infinite). Its [[variance]] is |
|||
:<math>\mathrm{var}(X)=\left(\frac{x_\mathrm{m}}{k-1}\right)^2 \frac{k}{k-2}.</math> |
|||
(If <math>k \le 2</math>, the variance is infinite). The raw [[moment (mathematics)|moments]] are found to be |
|||
:<math>\mu_n'=\frac{kx_\mathrm{m}^n}{k-n}, \,</math> |
|||
but they are only defined for <math>k>n</math>. This means that the moment generating function, which is just a [[Taylor series]] in <math>x</math> with <math>\mu_n'/n!</math> as coefficients, is not defined. The characteristic function is given by |
|||
:<math>\varphi(t;k,x_\mathrm{m})=k(-ix_\mathrm{m} t)^k\Gamma(-k,-ix_\mathrm{m} t),</math> |
|||
where Γ(a,x) is the incomplete [[Gamma function]]. The Pareto distribution is related to the [[exponential distribution]] by |
|||
:<math>f(x;k,x_\mathrm{m})=\mathrm{Exponential}(\ln(x/x_\mathrm{m});k).\,</math> |
|||
The [[Dirac delta function]] is a limiting case of the Pareto distribution: |
|||
:<math>\lim_{k\rightarrow \infty} f(x;k,x_\mathrm{m})=\delta(x-x_\mathrm{m}). \, </math> |
|||
=== A characterization theorem === |
|||
Suppose ''X''<sub>''i''</sub>, ''i'' = 1, 2, 3, ... are [[independent identically distributed]] [[random variable]]s whose probability distribution is supported on the interval <nowiki>[</nowiki>''k'', ∞<nowiki>)</nowiki> for some ''k'' > 0. Suppose that for all ''n'', the two random variables min{ ''X''<sub>1</sub>, ..., ''X''<sub>''n''</sub> } and (''X''<sub>1</sub> + ... + ''X''<sub>''n''</sub>)/min{ ''X''<sub>1</sub>, ..., ''X''<sub>''n''</sub> } are independent. Then the common distribution is a Pareto distribution. |
|||
=== Relation to Zipf's law === |
|||
Pareto distributions are continuous probability distributions. [[Zipf's law]], also sometimes called the [[zeta distribution]], may be thought of as a discrete counterpart of the Pareto distribution. |
|||
== Pareto, Lorenz, and Gini == |
|||
[[Image:Pareto_distributionLorenz.png|thumb|325px|Lorenz curves for a number of Pareto distributions. The ''k'' = ∞ corresponds to perfectly equal distribution (''G'' = 0) and the ''k'' = 1 line corresponds to complete inequality (''G'' = 1) ]] |
|||
The [[Lorenz curve]] is often used to characterize income and wealth |
|||
distributions. For any distribution, the Lorenz curve ''L''(''F'') is written |
|||
in terms of the PDF <math>(f(x))</math> or the CDF <math>(F(x))</math> as |
|||
:<math>L(F)=\frac{\int_{x_\mathrm{m}}^{x(F)} |
|||
xf(x)\,dx}{\int_{x_\mathrm{m}}^\infty xf(x)\,dx} |
|||
=\frac{\int_0^F x(F')\,dF'}{\int_0^1 x(F')\,dF'}</math> |
|||
where ''x''(''F'') is the inverse of the CDF. For the Pareto distribution, |
|||
:<math>x(F)=\frac{x_\mathrm{m}}{(1-F)^{1/k}}</math> |
|||
and the Lorenz curve is calculated to be |
|||
:<math>L(F) = 1-(1-F)^{1-1/k},\,</math> |
|||
where ''k'' must be greater than or equal to unity, since the denominator in the expression for ''L''(''F'') is just the mean value of ''x''. Examples of the Lorenz curve for a number of Pareto distributions are shown in the graph on the right. |
|||
The [[Gini coefficient]] is a measure of the deviation of the Lorenz curve from the equidistribution line which is a line connecting [0,0] and [1,1], which is shown in black (''k'' = ∞) in the Lorenz plot on the right. Specifically, the Gini coefficient is twice the area between the Lorenz curve and the equidistribution line. The Gini coefficient for the Pareto distribution is then calculated to be |
|||
:<math>G = 1-2\int_0^1L(F)\,dF = \frac{1}{2k-1}</math> |
|||
(see Aaberge 2005). |
|||
== Parameter estimation == |
|||
The [[likelihood function]] for the Pareto distribution parameters ''k'' and <math>x_\mathrm{m}</math>, given a [[sample (statistics)|sample]] <math>x = (x_1, x_2, \dots, x_n)</math>, is |
|||
: <math>L(k, x_\mathrm{m}) = \prod _{i=1} ^n {k \frac {x_\mathrm{m}^k} {x_i^{k+1}}} = k^n x_\mathrm{m}^{nk} \prod _{i=1} ^n {\frac 1 {x_i^{k+1}}}. \!</math> |
|||
Therefore, the logarithmic likelihood function is |
|||
: <math>\ell(k, x_\mathrm{m}) = n \ln k + nk \ln x_\mathrm{m} - (k + 1) \sum _{i=1} ^n {\ln x_i}. \!</math> |
|||
It can be seen that <math>\ell(k, x_\mathrm{m})</math> is monotonically increasing with <math>x_\mathrm{m}</math>, that is, the greater the value of <math>x_\mathrm{m}</math>, the greater the value of the likelihood function. Hence, since <math>x \ge x_\mathrm{m}</math>, we conclude that |
|||
: <math>\widehat x_\mathrm{m} = \min _i {x_i}.</math> |
|||
To find the [[estimator]] for ''k'', we compute the corresponding partial derivative and determine where it is zero: |
|||
: <math>\frac{\partial \ell}{\partial k} = \frac{n}{k} + n \ln x_\mathrm{m} - \sum _{i=1} ^n {\ln x_i} = 0.</math> |
|||
Thus the [[maximum likelihood]] estimator for ''k'' is: |
|||
: <math>\widehat k = \frac n {\sum _i {\left( \ln x_i - \ln \widehat x_\mathrm{m} \right)}}.</math> |
|||
The expected statistical error is: |
|||
: <math>\sigma = \frac {\widehat k} {\sqrt n}. </math> [http://aps.arxiv.org/PS_cache/cond-mat/pdf/0412/0412004v3.pdf] |
|||
==Graphical representation== |
|||
The charateristic curved '[[long tail]]' distribution when plotted on a linear scale, masks the underlying simplicity of the function when plotted on a log-log graph, which then takes the form of a straight line with negative gradient. |
|||
== Generating a random sample from Pareto distribution == |
|||
The Pareto distribution is not yet recognized by many [[programming language]]s. In the [[actuarial]] field, the Pareto distribution is widely used to estimate portfolio costs. As a matter of fact, it can be quite demanding to get data from this particular [[probability distribution]]. One can easily generate a [[random sample]] from Pareto distribution by mixing two [[random variable]]s, which are usually built-in in many statistical tools. The process is quite simple; one has to generate numbers from an [[exponential distribution]] with its λ equal to a random generated sample from a [[gamma distribution]] |
|||
: <math>\displaystyle k_\mathrm{Gamma}=k_\mathrm{Pareto}\, </math> |
|||
and |
|||
: <math>\theta_\mathrm{Gamma}=\frac1{x_{\mathrm{m}_\mathrm{Pareto}}}.</math> |
|||
This process generates data starting at 0, so then we need to add <math>x_\mathrm{m}</math>. |
|||
Alternatively, random samples can be generated using [[inverse transform sampling]]. Given a random variate <math>U</math> drawn from the [[uniform distribution (continuous)|uniform distribution]] on the unit interval <math>(0; 1)</math>, the variate |
|||
:<math>T=\frac{x_\mathrm{m}}{U^{1/k}}</math> |
|||
is Pareto-distributed. [http://www.stat.psu.edu/~dhunter/R/2006mle.html] |
|||
== Generalized Pareto distribution == |
|||
The family of '''generalized Pareto distributions (GPD)''' has three parameters <math> \mu,\sigma \,</math> and <math> \xi \,</math>. |
|||
{{Probability distribution | |
|||
name =Generalized Pareto | |
|||
type =density| |
|||
pdf_image =| |
|||
cdf_image =| |
|||
parameters = |
|||
<math>\mu \in (-\infty,\infty) \,</math> [[location parameter|location]] ([[real numbers|real]])<br /> |
|||
<math>\sigma \in (0,\infty) \,</math> [[scale parameter|scale]] (real)<br /> |
|||
<math>\xi\in (-\infty,\infty) \,</math> [[shape parameter|shape]] (real)| |
|||
support =<math>x \geqslant \mu\,\;(\xi \geqslant 0)</math><br /> |
|||
<math>\mu \leqslant x \leqslant \mu-\sigma/\xi\,\;(\xi < 0)</math>| |
|||
pdf =<math>\frac{1}{\sigma}(1 + \xi z )^{-(1/\xi +1)} </math><br /> |
|||
where <math>z=\frac{x-\mu}{\sigma}</math>| |
|||
cdf =<math>1-(1+\xi z)^{-1/\xi} \,</math>| |
|||
mean =<math>\mu + \frac{\sigma}{1-\xi}\, \; (\xi < 1) </math>| |
|||
median =<math>\mu + \frac{\sigma( 2^{\xi} -1)}{\xi} </math>| |
|||
mode =| |
|||
variance =<math>\frac{\sigma^2}{(1-\xi)^2(1-2\xi)}\, \; (\xi < 1/2) </math>| |
|||
skewness =| |
|||
kurtosis =| |
|||
entropy =| |
|||
mgf =| |
|||
char =| |
|||
}} |
|||
The [[cumulative distribution function]] is |
|||
: <math>F_{(\xi,\mu,\sigma)}(x) = 1 - \left(1+ \frac{\xi(x-\mu)}{\sigma}\right)^{-1/\xi}</math> |
|||
for <math> x \geqslant \mu </math>, and <math> x \leqslant \mu - \sigma /\xi </math> when <math> \xi < 0 \,</math> , where <math>\mu\in\mathbb R</math> is the location parameter, <math>\sigma>0 \,</math> the scale parameter and <math>\xi\in\mathbb R</math> the shape parameter. Note that some references give the "shape parameter" as <math> \kappa = - \xi \,</math>. |
|||
The [[probability density function]] is |
|||
: <math>f_{(\xi,\mu,\sigma)}(x) = \frac{1}{\sigma}\left(1 + \frac{\xi (x-\mu)}{\sigma}\right)^{\left(-\frac{1}{\xi} - 1\right)}.</math> |
|||
again, for <math> x \geqslant \mu </math>, and <math> x \leqslant \mu - \sigma /\xi </math> when <math> \xi < 0 \,</math> . |
|||
== Generating generalized Pareto random variables == |
|||
If ''U'' is [[uniform distribution (continuous)|uniformly distributed]] on |
|||
(0, 1<nowiki>]</nowiki>, then |
|||
:<math> X = \mu + \frac{\sigma (U^{-\xi}-1)}{\xi} \sim \mbox{GPD}(\mu,\sigma,\xi). </math> |
|||
{{Expand-section|date=January 2007}} |
|||
==Annotations== |
|||
{{reflist}} |
|||
==References== |
|||
* Lorenz, M. O. (1905). Methods of measuring the concentration of wealth. Publications of the American Statistical Association. 9: 209–219. |
|||
==See also== |
|||
* [[Pareto principle]] |
|||
* [[Pareto interpolation]] |
|||
* [[Pareto efficiency]] |
|||
* [[Pareto analysis]] |
|||
* [[The Long Tail]] |
|||
==External links== |
|||
* The Pareto, Zipf and other power laws / William J. Reed -- [http://linkage.rockefeller.edu/wli/zipf/reed01_el.pdf PDF] |
|||
* Gini's Nuclear Family / Rolf Aabergé. -- In: [http://www.unisi.it/eventi/GiniLorenz05/ International Conference to Honor Two Eminent Social Scientists], May, 2005 -- [http://www.unisi.it/eventi/GiniLorenz05/25%20may%20paper/PAPER_Aaberge.pdf PDF] |
|||
* The [[SOCR]] Resource provides [http://socr.ucla.edu/htmls/SOCR_Distributions.html interactive interface to Pareto distribution] and [http://socr.ucla.edu/htmls/SOCR_Modeler.html Pareto sampling and simulation]. |
|||
{{ProbDistributions|continuous-semi-infinite}} |
|||
[[Category:Continuous distributions]] |
|||
[[Category:Power laws]] |
|||
[[Category:Socioeconomics]] |
|||
[[de:Pareto-Verteilung]] |
|||
[[es:Distribución Pareto]] |
|||
[[fi:Pareto-jakauma]] |
|||
[[fr:Distribution de Pareto]] |
|||
[[it:Variabile casuale paretiana]] |
|||
[[nl:Paretoverdeling]] |
|||
[[pl:Rozkład Pareto]] |
|||
[[ru:Распределение Парето]] |
|||
[[tr:Pareto dağılımı]] |
|||
[[uk:Розподіл Парето]] |
|||
[[zh:帕累托分布]] |
|||
Revision as of 11:24, 21 June 2008
|
Probability density function  Pareto probability density functions for various k with xm = 1. The horizontal axis is the x parameter. As k → ∞ the distribution approaches δ(x − xm) where δ is the Dirac delta function. | |||
|
Cumulative distribution function  Pareto cumulative distribution functions for various k with xm = 1. The horizontal axis is the x parameter. | |||
| Parameters |
scale (real) shape (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | for | ||
| Median | |||
| Mode | |||
| Variance | for | ||
| Skewness | for | ||
| Excess kurtosis | for | ||
| Entropy | |||
| MGF | undefined; see text for raw moments | ||
| CF | |||
The Pareto distribution, named after the Italian economist Vilfredo Pareto, is a power law probability distribution that coincides with social, scientific, geophysical, actuarial, and many other types of observable phenomena. Outside the field of economics it is at times referred to as the Bradford distribution.
Pareto originally used this distribution to describe the allocation of wealth among individuals since it seemed to show rather well the way that a larger portion of the wealth of any society is owned by a smaller percentage of the people in that society. This idea is sometimes expressed more simply as the Pareto principle or the "80-20 rule" which says that 20% of the population owns 80% of the wealth[1]. It can be seen from the probability density function (PDF) graph on the right, that the "probability" or fraction of the population that owns a small amount of wealth per person (x) is rather high, and then decreases steadily as wealth increases. This distribution is not limited to describing wealth or income distribution, but to many situations in which an equilibrium is found in the distribution of the "small" to the "large". The following examples are sometimes seen as approximately Pareto-distributed:
- The sizes of human settlements (few cities, many hamlets/villages)
- File size distribution of Internet traffic which uses the TCP protocol (many smaller files, few larger ones)
- Clusters of Bose-Einstein condensate near absolute zero
- The values of oil reserves in oil fields (a few large fields, many small fields)
- The length distribution in jobs assigned supercomputers (a few large ones, many small ones)
- The standardized price returns on individual stocks
- Sizes of sand particles
- Sizes of meteorites
- Numbers of species per genus (There is subjectivity involved: The tendency to divide a genus into two or more increases with the number of species in it)
- Areas burnt in forest fires
- Severity of large casualty losses for certain lines of business such as general liability, commercial auto, and workers compensation.
Properties
Definition
If X is a random variable with a Pareto distribution, then the probability that X is greater than some number x is given by
for all x ≥ xm, where xm is the (necessarily positive) minimum possible value of X, and k is a positive parameter. The family of Pareto distributions is parameterized by two quantities, xm and k. When this distribution is used to model the distribution of wealth, then the parameter k is called the Pareto index.
Density function
It follows that the probability density function is
Various properties
The expected value of a random variable following a Pareto distribution is
(if k ≤ 1, the expected value is infinite). Its variance is
(If , the variance is infinite). The raw moments are found to be
but they are only defined for . This means that the moment generating function, which is just a Taylor series in with as coefficients, is not defined. The characteristic function is given by
where Γ(a,x) is the incomplete Gamma function. The Pareto distribution is related to the exponential distribution by
The Dirac delta function is a limiting case of the Pareto distribution:
A characterization theorem
Suppose Xi, i = 1, 2, 3, ... are independent identically distributed random variables whose probability distribution is supported on the interval [k, ∞) for some k > 0. Suppose that for all n, the two random variables min{ X1, ..., Xn } and (X1 + ... + Xn)/min{ X1, ..., Xn } are independent. Then the common distribution is a Pareto distribution.
Relation to Zipf's law
Pareto distributions are continuous probability distributions. Zipf's law, also sometimes called the zeta distribution, may be thought of as a discrete counterpart of the Pareto distribution.
Pareto, Lorenz, and Gini
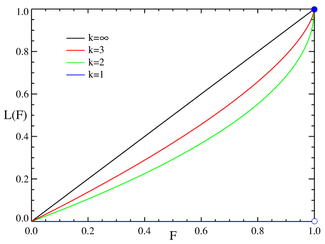
The Lorenz curve is often used to characterize income and wealth distributions. For any distribution, the Lorenz curve L(F) is written in terms of the PDF or the CDF as
where x(F) is the inverse of the CDF. For the Pareto distribution,
and the Lorenz curve is calculated to be
where k must be greater than or equal to unity, since the denominator in the expression for L(F) is just the mean value of x. Examples of the Lorenz curve for a number of Pareto distributions are shown in the graph on the right.
The Gini coefficient is a measure of the deviation of the Lorenz curve from the equidistribution line which is a line connecting [0,0] and [1,1], which is shown in black (k = ∞) in the Lorenz plot on the right. Specifically, the Gini coefficient is twice the area between the Lorenz curve and the equidistribution line. The Gini coefficient for the Pareto distribution is then calculated to be
(see Aaberge 2005).
Parameter estimation
The likelihood function for the Pareto distribution parameters k and , given a sample , is
Therefore, the logarithmic likelihood function is
It can be seen that is monotonically increasing with , that is, the greater the value of , the greater the value of the likelihood function. Hence, since , we conclude that
To find the estimator for k, we compute the corresponding partial derivative and determine where it is zero:
Thus the maximum likelihood estimator for k is:
The expected statistical error is:
Graphical representation
The charateristic curved 'long tail' distribution when plotted on a linear scale, masks the underlying simplicity of the function when plotted on a log-log graph, which then takes the form of a straight line with negative gradient.
Generating a random sample from Pareto distribution
The Pareto distribution is not yet recognized by many programming languages. In the actuarial field, the Pareto distribution is widely used to estimate portfolio costs. As a matter of fact, it can be quite demanding to get data from this particular probability distribution. One can easily generate a random sample from Pareto distribution by mixing two random variables, which are usually built-in in many statistical tools. The process is quite simple; one has to generate numbers from an exponential distribution with its λ equal to a random generated sample from a gamma distribution
and
This process generates data starting at 0, so then we need to add .
Alternatively, random samples can be generated using inverse transform sampling. Given a random variate drawn from the uniform distribution on the unit interval , the variate
is Pareto-distributed. [2]
Generalized Pareto distribution
The family of generalized Pareto distributions (GPD) has three parameters and .
| Parameters | shape (real) | ||
|---|---|---|---|
| Support |
| ||
|
| |||
| CDF | |||
| Mean | |||
| Median | |||
| Variance | |||
The cumulative distribution function is
for , and when , where is the location parameter, the scale parameter and the shape parameter. Note that some references give the "shape parameter" as .
The probability density function is
again, for , and when .
Generating generalized Pareto random variables
If U is uniformly distributed on (0, 1], then
This section needs expansion. You can help by adding to it. (January 2007) |
Annotations
- ^ For a two-quantile population, where 18% of the population owns 82% of the wealth, the Theil index takes the value 1.
References
- Lorenz, M. O. (1905). Methods of measuring the concentration of wealth. Publications of the American Statistical Association. 9: 209–219.
See also
External links
- The Pareto, Zipf and other power laws / William J. Reed -- PDF
- Gini's Nuclear Family / Rolf Aabergé. -- In: International Conference to Honor Two Eminent Social Scientists, May, 2005 -- PDF
- The SOCR Resource provides interactive interface to Pareto distribution and Pareto sampling and simulation.








![{\displaystyle x_{\mathrm {m} }{\sqrt[{k}]{2}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/8fdf86cbd7a8836f29913933cfb612965cc708e5)

































































