Magnetic circular dichroism: Difference between revisions
Zhanyong.li (talk | contribs) |
Zhanyong.li (talk | contribs) |
||
| Line 7: | Line 7: | ||
==Applicable Cases== |
==Applicable Cases== |
||
MCD can be used as an optical technique for the detection of electronic structure of both the ground states and excited states. It is also a strong addition to the more commonly used absorption spectroscopy, and there are two reasons that explain this. First, a transition buried under a stronger transition can appear in MCD if the first derivative of the absorption is much larger for the weaker transition or it is of the opposite sign. Second, MCD will be found where no absorption is detected at all if ΔA > (ΔA<sub>min</sub>) but A<A<sub>min</sub>, where (ΔA)<sub>min</sub> and A<sub>min</sub> are the minimum of ΔA and A that are detectable. Typically, (ΔA<sub>min</sub>) and A<sub>min</sub> are of the magnitudes around 10<sup>-5</sup> and 10<sup>-3</sup> respectively. So, a transition can only be detected in MCD, not in the absorption spectroscopy, if ΔA/A > 10<sup>-2</sup>. This happens in paramagnetic systems that are at lower temperature or that have sharp lines in the spectroscopy. |
MCD can be used as an optical technique for the detection of electronic structure of both the ground states and excited states. It is also a strong addition to the more commonly used absorption spectroscopy, and there are two reasons that explain this. First, a transition buried under a stronger transition can appear in MCD if the first derivative of the absorption is much larger for the weaker transition or it is of the opposite sign. Second, MCD will be found where no absorption is detected at all if ΔA > (ΔA<sub>min</sub>) but A<A<sub>min</sub>, where (ΔA)<sub>min</sub> and A<sub>min</sub> are the minimum of ΔA and A that are detectable. Typically, (ΔA<sub>min</sub>) and A<sub>min</sub> are of the magnitudes around 10<sup>-5</sup> and 10<sup>-3</sup> respectively. So, a transition can only be detected in MCD, not in the absorption spectroscopy, if ΔA/A > 10<sup>-2</sup>. This happens in paramagnetic systems that are at lower temperature or that have sharp lines in the spectroscopy. |
||
<ref>solomon or whatever</ref> |
|||
==Differences between [[Circular Dichroism|CD]] and MCD== |
==Differences between [[Circular Dichroism|CD]] and MCD== |
||
Revision as of 18:50, 15 April 2010
Magnetically induced circular dichroism (MCD) is the differential absorption of left and right circularly polarized light, induced in a sample by a strong magnetic field oriented parallel to the direction of light propagation. In general, this means wrapping a circular dichrometer in a large electromagnet. If the magnet is water cooled, field strength of a couple of teslas are common. With a superconducting magnet, field strengths can reach 7 Teslas.
It was first shown by Faraday that optical activity could be induced in matter by a longitude magnetic field. The development of MCD really began in the 1930s when a quantum mechanical theory of MOR (magnetic optical rotatory dispersion) in regions outside absorption bands was formulated. The expansion of the theory to include MCD and MOR effects in the region of absorptions, which were referred to as “anomalous dispersions” was developed soon thereafter. There was, however, little effort made to refine MCD as a modern spectroscopic technique until the early 1960s. Since that time there have been numerous studies of MCD spectra for a very large variety of samples, including stable molecules in solutions, in isotropic solids, and in the gas phase, as well as unstable molecules entrapped in noble gas matrices. More recently, MCD has found useful application in the study of biologically important systems including metalloenzymes and proteins containing metal centers.
The main focus of the MCD is to analyze the A, B, C terms of the spectra. Principles and examples will be explained later on this page.
Applicable Cases
MCD can be used as an optical technique for the detection of electronic structure of both the ground states and excited states. It is also a strong addition to the more commonly used absorption spectroscopy, and there are two reasons that explain this. First, a transition buried under a stronger transition can appear in MCD if the first derivative of the absorption is much larger for the weaker transition or it is of the opposite sign. Second, MCD will be found where no absorption is detected at all if ΔA > (ΔAmin) but A<Amin, where (ΔA)min and Amin are the minimum of ΔA and A that are detectable. Typically, (ΔAmin) and Amin are of the magnitudes around 10-5 and 10-3 respectively. So, a transition can only be detected in MCD, not in the absorption spectroscopy, if ΔA/A > 10-2. This happens in paramagnetic systems that are at lower temperature or that have sharp lines in the spectroscopy.
Differences between CD and MCD
In natural optical activity, the difference between the lcp light and the rcp light is caused by the dissymmetry of the molecules. Due to the handedness of the molecule, the absorption of the lcp light would be different from the rcp light. However, in MCD in the presence of a magnetic field, lcp and rcp no longer interact equivalently with the absorbing medium. Thus there is not the same direct relation between magnetic optical activity and molecular stereochemistry which would be expected, because it is found in natural optical activity. So, natural CD is a relatively rare phenomenon, while MCD is a property of all matter.
Spectrometer
Modern day spectrometers can achieve simultaneous measurement of absorbance and the MCD ΔA along the same light path. This eliminates error introduced through multiple measurements or different instruments that previously occurred before this advent. A MCD spectrometer begins with a light source that emits a monochromatic wave of light. This wave is passed through a Rochon prisim linear polarizer, which separates the incident wave into two beams that are linearly polarized by 90 degrees. The two beams split into different paths- one beam (the extraordinary beam) traveling directly to a photomultiplier (PMT), and the other beam (the ordinary beam) passing through a photoelastic modulator (PEM). The PMT for the extraordinary beam detects the light intensity of the input beam, while the PEM causes a 1/4 wavelength shift that converts linearly polarized light into circularly polarized light. Linearly polarized light has two circular components with intensity represented by: File:Formula for intensity.png
The PEM will delay one component of linearly polarized light with a time dependence that advances the other component by 1/4 λ (hence, quarter-wave shift). The departing circularly polarized light oscillates between rcp and lcp in a sinusoidal time-dependence as depicted below:
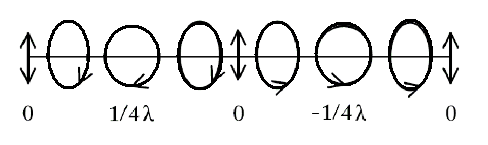
The light finally travels through a magnet containing the sample, and the transmittance is recorded by another PMT. The schematic is given below:

The intensity of light from the ordinary wave that reaches the PMT is governed by the equation: File:Formula for the difference of the intensity.png
A- and A+ are the absorbances of lcp or rcp, respectively; ω is the modulator frequency- usually a high acoustic frequency such as 50 kHz; t is time; and δ0 is the time dependent wavelength shift.
This intensity of light passing through the sample is converted into a two component voltage via a current/voltage amplifier. A DC voltage will emerge corresponding to the intensity of light passed through the sample. If there is a ΔA, then a small AC voltage with be present that corresponds to the modulation frequency, ω. From such voltage, ΔA and A can be derived using the following relations: File:The measument of det A.png
where Vex is the voltage measured by the PMT from the extraordinary wave.
File:MCD actual instrument.jpg
Photograph given by permission of a low-temperature MCD Spectrometer Built at the University of Michigan.
MCD signals tend to be small, so the measurements often take time. To get a reasonable signal to noise ratio, the experiments can often take a few hours. Multiple spectra are often taken, digitized, accumulated and stored via computer. Although there is much overlap in the requirements and use of instruments, ordinary CD instruments are usually optimized for operation in the ultraviolet, approximately 170–300 nm, while MCD instruments are typically required to operate in the visible to near infrared, approximately 300–2000 nm.
The physical processes that lead to MCD are substantively different from those of CD. However, like CD, it is dependent on the differential absorption of left and right hand circularly polarized light. MCD will only exist at a given wavelength if the molecule has an optical absorption at that wavelength. This is distinctly different from the related phenomenon of Optical Rotatory Dispersion (ORD), which can be observed at wavelengths far from any absorption band.
Some superconducting magnets have a small sample chamber, far too small to contain the entire optical system. Instead, the magnet sample chamber has windows on two opposite sides. Light from the source enters one side, interacts with the sample (usually also temperature controlled) in the magnetic field, and exits through the opposite window to the detector. Optical relay systems that allow the source and detector each to be about a meter from the sample are typically employed. This arrangement avoids many of the difficulties that would be encountered if the optical apparatus had to operate in the high magnetic field, and also allows for a much less expensive magnet.
How it works
Basically, we consider the systems are of localized, non-interacting absorbing centers. Based on the semi-classical radiation absorption theory within the electric dipole approximation, the electric vector of the Circular Polarized waves propagates in the + z direction, where + and -denote to rcp light and lcp light respectively.
In this system, ω = 2nν is the circular frequency, and Ii = n-ik is the complex refractive index. As the light travels, the attenuation of the beam is expressed by
File:Intensity as the light travels.png
in which k means the absorption coefficient of the medium in the z direction Circular Dichroism (CD) is then defined through
File:Different absorpsion in terms of k.png
And it follows the sign convention of natural optical activity. In the presence of the static, uniform external magnetic field, The Hamiltonian for the absorbing center is of the form
File:Hamiltonian of the state in MCD.png
which is parallel to the direction of the propagation of the electric field k. Due to the transition between the two eigenstates of H0, a and j, the absorption and the CD intensity would be determined as follows:
File:Intensity in terms of k.png
Discrete line spectrum
In a certain frequency range, if the transitions of the absorbing centers are relatively sparse, the absorption spectrum in this region would be of a series of lines. Each line would correspond to a single transition and be either completely or partially resolved from neighboring lines.
Since it is of the discrete form, then the absorption coefficient and CD of the line are given by

When the Zeeman Effect is small compared to zero-field state separations, line width, and kT and when the line shape is independent of H, it could be obtain to first order in H for the expression of Δk, assuming J to be sufficiently high in energy that Nj = 0. And it is given by:

Δk is the field-dependent difference between lcp and rcp absorption, α is the electric permeability, n is the index of refraction, and H is the applied magnetic field, k is the Boltzmann constant and T is the temperature. Further, f is a band shape function and f’ is the correspondent first derivative. D is the dipole strength parameter, and it is defined as File:Definition of D term.png
There are various form of the formulas above. A more common form is in terms of A (absorption), which would be:

The constants A, B, and C are characteristic parameters specific to a given molecule and to a particular transition, which are referred to as A, B, and C terms, respectively, a nomenclature introduced by Stephens and dating back to Serber's early theory of MOR.

A term arises due to Zeeman splitting of the ground or excited degenerate states, like what is shown in the (2) in Figure 1 The small Zeeman splitting would make the oppositely signed transitions rcp light and lcp light almost cancel out with each other, which leads to the derivative shape of the band. B term is due to the field-induced mixing of states. As shown in (3) of the Figure 1, in order for there to be an appearance of B term, there must be another state K, which is closely related in energy to either the ground state or the excited states. Also, the energy between the ground state and the excited state should be high enough so that the excited state is not highly populated. Ususally, B term would have the absorption band shape. Otherwise, it will lead to the C term (4) of Figure 1, which requires the degeneracy of the ground state. This happens due to a change in the population of molecules over the Zeeman sublevels of a paramagnetic ground state. In addition, the C term is observed only for molecules with ground state paramagnetism. Importantly, A and B terms are independent of temperature while the C term is dependent on temperature. Decrease of the temperature and increase of the magnetic field would further increase the C term intensity until it reaches the maximum(saturation limit). Experimentally, the C term spectrum can be obtained from MCD raw data by substraction of MCD spectra measured in the same applied magnetic field at different temperatures, while A and B terms can be distinguished via their different band shapes. The relative contributions of A, B and C terms to the MCD spectrum are proportional to the inverse line width, energy splitting, and temperature:
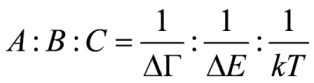
in which, ΔΓ is line width and ΔE is zero-field state separation magnitudes. Typically, the values (ΔГ= 1000 cm-1, ΔE = 10,000 cm-1 , and kT = 6 cm-1 (at 10 K), the three terms will make relative contributions 1:0.1:150. So, at low temperature the C term will dominate over A and B term.
Examples
In the visible and near-ultraviolet regions, the hexacyanoferrate(III) ion exhibits three strong transitions, which have been ascribed to Ligand to Metal Charge Transfer (LMCT) transitions. The three intense bands are located at 24500, 32700, and 40500 cm-1 in the spectra of the Fe (III) complex Fe(CN)63-, which are all found lower in energy than the lowest energy intense band for the Fe(II) complex Fe(CN)62- found at 46000 cm-1. The red shift as the oxidation state of the metal increases is characteristic of LMCT bands.
 File:Example C term figure 3.png
File:Example C term figure 3.png
The dependence of the C term of MCD is explored here. The ground state of the anion is 2T2g, which derives from the electronic configuration (t2g)5. So, there would be an unpaired electron in the d orbital of Fe3+ From that, we can assign the three bands correspondent to the transitions 2t2g→2t1u1, 2t2g →2t1u2, 2t2g →2t2u. Noticed that two of the excited states are of the same symmetry, and based on the group theory, we can assert that they would actually mix with each other so that there are no pure σ, π character of the two t1u states, but for t2u, there would be no inter-mixing. It should be noted that A terms are also possible from the degenerate excited states, but the temperature-dependence studies showed that they are not as dependent as the C term.
File:Example C term figure 4(2).png
A more recent study was done on the MCD of Fe(CN)63- embedded in a thin poly(vinyl alcohol) (PVA) film. We can clearly see that there is a dependence on temperature by the C term. With the equations that were given in the theory part, we can get the appropriate expression for C0 and D0. The observed values of C0/D0 at room temperature for the three bands in the Fe(CN)63- spectrum are 1.2, -0.6, and 0.6 (with some experimental uncertainty in the last two values) respectively. Thus the signs we got from the experiment for the three C terms in the MCD spectra (positive, negative, and positive) establish the energy ordering as: 2t2g→2t1u2<2t2g→2t2u<2t2g→2t1u1
Spectra
In the most common kind of MCD (the so-called A spectra), the magnetic field breaks the degeneracy of excited state optical energy levels differing only in magnetic spin. This separation is small, leading to tiny shifts in frequency in otherwise nearly identical spectra, that, because of different signs of the spin state, are opposite in sign. As a consequence, these kinds of MCD absorption spectra (so called A spectra) are shaped like a frequency derivative of the underlying optical spectra, having a peak on one side of the related optical maximum and a trough on the other side.
In type C spectra, MCD absorption is a consequence of the magnetic field breaking the degeneracy of the ground state of the optical absorption. Unlike A spectra, the intensity of C spectra are affected by temperature, with stronger signals being observed as the sample is cooled. For samples exhibiting both A and C class spectra, taking the MCD as a function of temperature is a way to separate the relative contributions of these two effects.
Other fields
In biology, metalloproteins are the most likely candidates for MCD measurements, as the presence of metals with degenerate energy levels leads to strong MCD signals. In the case of ferric hemoproteins, MCD is capable of determining both oxidation and spin state to a remarkably exquisite degree. In regular proteins, MCD is capable of stoichiometrically measuring the tryptophan content of proteins, assuming there are no other competing absorbers in the spectroscopic system.
