Wallpaper group: Difference between revisions
Removed duplicate "cell structure" images for sections that do not use template:wallpaper_group_list |
Converted all sections to use template::wallpaper_group_list |
||
| Line 268: | Line 268: | ||
Ignoring the wavy borders of the tiles, the pavement is [[#Group pgg|'''pgg''']]. |
Ignoring the wavy borders of the tiles, the pavement is [[#Group pgg|'''pgg''']]. |
||
{{-}} |
|||
===Group cm=== |
===Group cm=== |
||
| ⚫ | |||
[[Image:Wallpaper group diagram cm.svg|left|thumb|Cell structure for '''cm''']] |
|||
| ⚫ | |||
* Orbifold notation: '''*x'''. |
|||
| ⚫ | |||
| ⚫ | |||
<br style="clear:both;"> |
|||
'''Examples of group ''cm''''' |
|||
<gallery> |
<gallery> |
||
Image:WallpaperCM.GIF|<center>Computer generated</center> |
Image:WallpaperCM.GIF|<center>Computer generated</center> |
||
| Line 327: | Line 321: | ||
===Group cmm=== |
===Group cmm=== |
||
| ⚫ | |||
[[Image:Wallpaper group diagram cmm.svg|left|thumb|Cell structure for '''cmm''']] |
|||
* Orbifold notation: '''2*22'''. |
|||
| ⚫ | |||
*This group is frequently seen in everyday life, since the most common arrangement of [[brick]]s in a brick building utilises this group (see example below). |
*This group is frequently seen in everyday life, since the most common arrangement of [[brick]]s in a brick building utilises this group (see example below). |
||
| Line 337: | Line 329: | ||
*symmetrically staggered rows of identical doubly symmetric objects |
*symmetrically staggered rows of identical doubly symmetric objects |
||
*a checkerboard pattern of two alternating rectangular tiles, of which each, by itself, is doubly symmetric |
*a checkerboard pattern of two alternating rectangular tiles, of which each, by itself, is doubly symmetric |
||
*a checkerboard pattern of alternatingly a 2-fold rotationally symmetric rectangular tile and its mirror image |
*a checkerboard pattern of alternatingly a 2-fold rotationally symmetric rectangular tile and its mirror image}} |
||
<br style="clear:both;"> |
|||
'''Examples of group ''cmm''''' |
|||
<gallery> |
<gallery> |
||
Image:WallpaperCMM.GIF|<center>Computer generated</center> |
Image:WallpaperCMM.GIF|<center>Computer generated</center> |
||
| Line 409: | Line 399: | ||
===Group p3=== |
===Group p3=== |
||
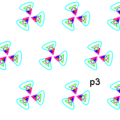
{{wallpaper_group_list|p3|333|* The group '''p3''' has three different rotation centres of order three (120°), but no reflections or glide reflections. |
|||
* Orbifold notation: '''333'''. |
|||
* The group '''p3''' has three different rotation centres of order three (120°), but no reflections or glide reflections. |
|||
Imagine a [[tessellation]] of the plane with equilateral triangles of equal size, with the sides corresponding to the smallest translations. Then half of the triangles are in one orientation, and the other half upside down. This wallpaper group corresponds to the case that all triangles of the same orientation are equal, while both types have rotational symmetry of order three, but the two are not equal, not each other's mirror image, and not both symmetric (if the two are equal we have p6, if they are each other's mirror image we have p31m, if they are both symmetric we have p3m1; if two of the three apply then the third also, and we have p6m). For a given image, three of these tessellations are possible, each with rotation centres as vertices, i.e. for any tessellation two shifts are possible. In terms of the image: the vertices can be the red, the blue or the green triangles. |
Imagine a [[tessellation]] of the plane with equilateral triangles of equal size, with the sides corresponding to the smallest translations. Then half of the triangles are in one orientation, and the other half upside down. This wallpaper group corresponds to the case that all triangles of the same orientation are equal, while both types have rotational symmetry of order three, but the two are not equal, not each other's mirror image, and not both symmetric (if the two are equal we have p6, if they are each other's mirror image we have p31m, if they are both symmetric we have p3m1; if two of the three apply then the third also, and we have p6m). For a given image, three of these tessellations are possible, each with rotation centres as vertices, i.e. for any tessellation two shifts are possible. In terms of the image: the vertices can be the red, the blue or the green triangles. |
||
Equivalently, imagine a tessellation of the plane with regular hexagons, with sides equal to the smallest translation distance divided by √3. Then this wallpaper group corresponds to the case that all hexagons are equal (and in the same orientation) and have rotational symmetry of order three, while they have no mirror image symmetry (if they have rotational symmetry of order six we have p6, if they are symmetric with respect to the main diagonals we have p31m, if they are symmetric with respect to lines perpendicular to the sides we have p3m1; if two of the three apply then the third also, and we have p6m). For a given image, three of these tessellations are possible, each with one third of the rotation centres as centres of the hexagons. In terms of the image: the centres of the hexagons can be the red, the blue or the green triangles. |
Equivalently, imagine a tessellation of the plane with regular hexagons, with sides equal to the smallest translation distance divided by √3. Then this wallpaper group corresponds to the case that all hexagons are equal (and in the same orientation) and have rotational symmetry of order three, while they have no mirror image symmetry (if they have rotational symmetry of order six we have p6, if they are symmetric with respect to the main diagonals we have p31m, if they are symmetric with respect to lines perpendicular to the sides we have p3m1; if two of the three apply then the third also, and we have p6m). For a given image, three of these tessellations are possible, each with one third of the rotation centres as centres of the hexagons. In terms of the image: the centres of the hexagons can be the red, the blue or the green triangles.}} |
||
<br style="clear:both;"> |
|||
'''Examples of group ''p3''''' |
|||
<gallery> |
<gallery> |
||
Revision as of 21:22, 21 March 2011

A wallpaper group (or plane symmetry group or plane crystallographic group) is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art. There are 17 possible distinct groups.
Wallpaper groups are two-dimensional symmetry groups, intermediate in complexity between the simpler frieze groups and the three-dimensional crystallographic groups (also called space groups).
Introduction
Wallpaper groups categorize patterns by their symmetries. Subtle differences may place similar patterns in different groups, while patterns that are very different in style, color, scale or orientation may belong to the same group.
Consider the following examples:
-
Example A: Cloth, Tahiti
Examples A and B have the same wallpaper group; it is called p4m. Example C has a different wallpaper group, called p4g. The fact that A and B have the same wallpaper group means that they have the same symmetries, regardless of details of the designs, whereas C has a different set of symmetries despite any superficial similarities.
A complete list of all seventeen possible wallpaper groups can be found below.
Symmetries of patterns
A symmetry of a pattern is, loosely speaking, a way of transforming the pattern so that the pattern looks exactly the same after the transformation. For example, translational symmetry is present when the pattern can be translated (shifted) some finite distance and appear unchanged. Think of shifting a set of vertical stripes horizontally by one stripe. The pattern is unchanged. Strictly speaking, a true symmetry only exists in patterns that repeat exactly and continue indefinitely. A set of only, say, five stripes does not have translational symmetry — when shifted, the stripe on one end "disappears" and a new stripe is "added" at the other end. In practice, however, classification is applied to finite patterns, and small imperfections may be ignored.
Sometimes two categorizations are meaningful, one based on shapes alone and one also including colors. When colors are ignored there may be more symmetry. In black and white there are also 17 wallpaper groups; e.g., a colored tiling is equivalent with one in black and white with the colors coded radially in a circularly symmetric "bar code" in the centre of mass of each tile.
The types of transformations that are relevant here are called Euclidean plane isometries. For example:
- If we shift example B one unit to the right, so that each square covers the square that was originally adjacent to it, then the resulting pattern is exactly the same as the pattern we started with. This type of symmetry is called a translation. Examples A and C are similar, except that the smallest possible shifts are in diagonal directions.
- If we turn example B clockwise by 90°, around the centre of one of the squares, again we obtain exactly the same pattern. This is called a rotation. Examples A and C also have 90° rotations, although it requires a little more ingenuity to find the correct centre of rotation for C.
- We can also flip example B across a horizontal axis that runs across the middle of the image. This is called a reflection. Example B also has reflections across a vertical axis, and across two diagonal axes. The same can be said for A.
However, example C is different. It only has reflections in horizontal and vertical directions, not across diagonal axes. If we flip across a diagonal line, we do not get the same pattern back; what we do get is the original pattern shifted across by a certain distance. This is part of the reason that the wallpaper group of A and B is different from the wallpaper group of C.
History
All 17 groups were used by Egyptian craftsmen[citation needed], and used extensively in the Muslim world. A proof that there were only 17 possible patterns was first carried out by Evgraf Fedorov in 1891[1] and then derived independently by George Pólya in 1924.[2][3]
Formal definition and discussion
Mathematically, a wallpaper group or plane crystallographic group is a type of topologically discrete group of isometries of the Euclidean plane that contains two linearly independent translations.
Two such isometry groups are of the same type (of the same wallpaper group) if they are the same up to an affine transformation of the plane. Thus e.g. a translation of the plane (hence a translation of the mirrors and centres of rotation) does not affect the wallpaper group. The same applies for a change of angle between translation vectors, provided that it does not add or remove any symmetry (this is only the case if there are no mirrors and no glide reflections, and rotational symmetry is at most of order 2).
Unlike in the three-dimensional case, we can equivalently restrict the affine transformations to those that preserve orientation.
It follows from the Bieberbach theorem that all wallpaper groups are different even as abstract groups (as opposed to e.g. Frieze groups, of which two are isomorphic with Z).
2D patterns with double translational symmetry can be categorized according to their symmetry group type.
Isometries of the Euclidean plane
Isometries of the Euclidean plane fall into four categories (see the article Euclidean plane isometry for more information).
- Translations, denoted by Tv, where v is a vector in R2. This has the effect of shifting the plane applying displacement vector v.
- Rotations, denoted by Rc,θ, where c is a point in the plane (the centre of rotation), and θ is the angle of rotation.
- Reflections, or mirror isometries, denoted by FL, where L is a line in R2. (F is for "flip"). This has the effect of reflecting the plane in the line L, called the reflection axis or the associated mirror.
- Glide reflections, denoted by GL,d, where L is a line in R2 and d is a distance. This is a combination of a reflection in the line L and a translation along L by a distance d.
The independent translations condition
The condition on linearly independent translations means that there exist linearly independent vectors v and w (in R2) such that the group contains both Tv and Tw.
The purpose of this condition is to distinguish wallpaper groups from frieze groups, which possess a translation but not two linearly independent ones, and from two-dimensional discrete point groups, which have no translations at all. In other words, wallpaper groups represent patterns that repeat themselves in two distinct directions, in contrast to frieze groups, which only repeat along a single axis.
(It is possible to generalise this situation. We could for example study discrete groups of isometries of Rn with m linearly independent translations, where m is any integer in the range 0 ≤ m ≤ n.)
The discreteness condition
The discreteness condition means that there is some positive real number ε, such that for every translation Tv in the group, the vector v has length at least ε (except of course in the case that v is the zero vector).
The purpose of this condition is to ensure that the group has a compact fundamental domain, or in other words, a "cell" of nonzero, finite area, which is repeated through the plane. Without this condition, we might have for example a group containing the translation Tx for every rational number x, which would not correspond to any reasonable wallpaper pattern.
One important and nontrivial consequence of the discreteness condition in combination with the independent translations condition is that the group can only contain rotations of order 2, 3, 4, or 6; that is, every rotation in the group must be a rotation by 180°, 120°, 90°, or 60°. This fact is known as the crystallographic restriction theorem, and can be generalised to higher-dimensional cases.
Notations for wallpaper groups
Crystallographic notation
Crystallography has 230 space groups to distinguish, far more than the 17 wallpaper groups, but many of the symmetries in the groups are the same. Thus we can use a similar notation for both kinds of groups, that of Carl Hermann and Charles-Victor Mauguin. An example of a full wallpaper name in Hermann-Mauguin style is p31m, with four letters or digits; more usual is a shortened name like cmm or pg.
For wallpaper groups the full notation begins with either p or c, for a primitive cell or a face-centred cell; these are explained below. This is followed by a digit, n, indicating the highest order of rotational symmetry: 1-fold (none), 2-fold, 3-fold, 4-fold, or 6-fold. The next two symbols indicate symmetries relative to one translation axis of the pattern, referred to as the "main" one; if there is a mirror perpendicular to a translation axis we choose that axis as the main one (or if there are two, one of them). The symbols are either m, g, or 1, for mirror, glide reflection, or none. The axis of the mirror or glide reflection is perpendicular to the main axis for the first letter, and either parallel or tilted 180°/n (when n > 2) for the second letter. Many groups include other symmetries implied by the given ones. The short notation drops digits or an m that can be deduced, so long as that leaves no confusion with another group.
A primitive cell is a minimal region repeated by lattice translations. All but two wallpaper symmetry groups are described with respect to primitive cell axes, a coordinate basis using the translation vectors of the lattice. In the remaining two cases symmetry description is with respect to centred cells that are larger than the primitive cell, and hence have internal repetition; the directions of their sides is different from those of the translation vectors spanning a primitive cell. Hermann-Mauguin notation for crystal space groups uses additional cell types.
Examples
- p2 (p211): Primitive cell, 2-fold rotation symmetry, no mirrors or glide reflections.
- p4g (p4gm): Primitive cell, 4-fold rotation, glide reflection perpendicular to main axis, mirror axis at 45°.
- cmm (c2mm): Centred cell, 2-fold rotation, mirror axes both perpendicular and parallel to main axis.
- p31m (p31m): Primitive cell, 3-fold rotation, mirror axis at 60°.
Here are all the names that differ in short and full notation.
Crystallographic short and full names Short p2 pm pg cm pmm pmg pgg cmm p4m p4g p6m Full p211 p1m1 p1g1 c1m1 p2mm p2mg p2gg c2mm p4mm p4gm p6mm
The remaining names are p1, p3, p3m1, p31m, p4, and p6.
Orbifold notation
Orbifold notation for wallpaper groups, introduced by John Horton Conway (Conway, 1992), is based not on crystallography, but on topology. We fold the infinite periodic tiling of the plane into its essence, an orbifold, then describe that with a few symbols.
- A digit, n, indicates a centre of n-fold rotation corresponding to a cone point on the orbifold. By the crystallographic restriction theorem, n must be 2, 3, 4, or 6.
- An asterisk, *, indicates a mirror symmetry corresponding to a boundary of the orbifold. It interacts with the digits as follows:
- A cross, x, occurs when a glide reflection is present and indicates a crosscap on the orbifold. Pure mirrors combine with lattice translation to produce glides, but those are already accounted for so we do not notate them.
- The "no symmetry" symbol, o, stands alone, and indicates we have only lattice translations with no other symmetry. The orbifold with this symbol is a torus; in general the symbol o denotes a handle on the orbifold.
Consider the group denoted in crystallographic notation by cmm; in Conway's notation, this will be 2*22. The 2 before the * says we have a 2-fold rotation centre with no mirror through it. The * itself says we have a mirror. The first 2 after the * says we have a 2-fold rotation centre on a mirror. The final 2 says we have an independent second 2-fold rotation centre on a mirror, one that is not a duplicate of the first one under symmetries.
The group denoted by pgg will be 22x. We have two pure 2-fold rotation centres, and a glide reflection axis. Contrast this with pmg, Conway 22*, where crystallographic notation mentions a glide, but one that is implicit in the other symmetries of the orbifold.
Conway and crystallographic correspondence Conway o xx *x ** 632 *632 Crystal. p1 pg cm pm p6 p6m Conway 333 *333 3*3 442 *442 4*2 Crystal. p3 p3m1 p31m p4 p4m p4g Conway 2222 22x 22* *2222 2*22 Crystal. p2 pgg pmg pmm cmm
Why there are exactly seventeen groups
An orbifold can be viewed as a polygon with face, edges, and vertices, which can be unfolded to form a possibly infinite set of polygons which tile either the sphere, the plane or the hyperbolic plane. When it tiles the plane it will give a wallpaper group and when it tiles the sphere or hyperbolic plane it gives either a spherical symmetry groups or Hyperbolic symmetry group. The type of space the polygons tile can be found by calculating the Euler characteristic, χ = V − E + F, where V is the number of corners (vertices), E is the number of edges and F is the number of faces. If the Euler characteristic is positive then the orbifold has a elliptic (spherical) structure; if it is zero then it has a parabolic structure, i.e. a wallpaper group; and if it is negative it will have a hyperbolic structure. When the full set of possible orbifolds is enumerated it is found that only 17 have Euler characteristic 0.
When an orbifold replicates by symmetry to fill the plane, its features create a structure of vertices, edges, and polygon faces, which must be consistent with the Euler characteristic. Reversing the process, we can assign numbers to the features of the orbifold, but fractions, rather than whole numbers. Because the orbifold itself is a quotient of the full surface by the symmetry group, the orbifold Euler characteristic is a quotient of the surface Euler characteristic by the order of the symmetry group.
The orbifold Euler characteristic is 2 minus the sum of the feature values, assigned as follows:
- A digit n before a * counts as (n−1)/n.
- A digit n after a * counts as (n−1)/2n.
- Both * and x count as 1.
- The "no symmetry" o counts as 2.
For a wallpaper group, the sum for the characteristic must be zero; thus the feature sum must be 2.
Examples
- 632: 5/6 + 2/3 + 1/2 = 2
- 3*3: 2/3 + 1 + 1/3 = 2
- 4*2: 3/4 + 1 + 1/4 = 2
- 22x: 1/2 + 1/2 + 1 = 2
Now enumeration of all wallpaper groups becomes a matter of arithmetic, of listing all feature strings with values summing to 2.
Incidentally, feature strings with other sums are not nonsense; they imply non-planar tilings, not discussed here. (When the orbifold Euler characteristic is negative, the tiling is hyperbolic; when positive, spherical or bad).
Guide to recognising wallpaper groups
To work out which wallpaper group corresponds to a given design, one may use the following table.
| Size of smallest rotation |
Has reflection? | |||||
|---|---|---|---|---|---|---|
| Yes | No | |||||
| 360° / 6 | p6m | p6 | ||||
| 360° / 4 | Has mirrors at 45°? | p4 | ||||
| Yes: p4m | No: p4g | |||||
| 360° / 3 | Has rot. centre off mirrors? | p3 | ||||
| Yes: p31m | No: p3m1 | |||||
| 360° / 2 | Has perpendicular reflections? | Has glide reflection? | ||||
| Yes | No | |||||
| Has rot. centre off mirrors? | pmg | Yes: pgg | No: p2 | |||
| Yes: cmm | No: pmm | |||||
| none | Has glide axis off mirrors? | Has glide reflection? | ||||
| Yes: cm | No: pm | Yes: pg | No: p1 | |||
See also this overview with diagrams.
The seventeen groups
Each of the groups in this section has two cell structure diagrams, which are to be interpreted as follows:
On the right-hand side diagrams, different equivalence classes of symmetry elements are colored (and rotated) differently.
The brown or yellow area indicates a fundamental domain, i.e. the smallest part of the pattern that is repeated.
The diagrams on the right show the cell of the lattice corresponding to the smallest translations; those on the left sometimes show a larger area.
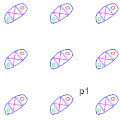
Group p1
-
Computer generated
The two translations (cell sides) can each have different lengths, and can form any angle.
Group p2
-
Computer generated -
Cloth, Sandwich Islands (Hawaii) -
Mat on which Egyptian king stood -
Egyptian mat (detail)
Group pm
(The first three have a vertical symmetry axis, and the last two each have a different diagonal one.)
-
Computer generated -
Dress of a figure in a tomb at Biban el Moluk, Egypt -
Indian metalwork at the Great Exhibition in 1851. This is almost pm (ignoring short diagonal lines between ovals motifs, which make it p1).
Group pg
-
Computer generated -
Mat with herringbone pattern on which Egyptian king stood -
Egyptian mat (detail) -
Pavement with herringbone pattern in Salzburg. Glide reflection axis runs northeast-southwest. -
One of the colorings of the snub square tiling; the glide reflection lines are in the direction upper left / lower right; ignoring colors there is much more symmetry than just pg, then it is p4g (see there for this image with equally colored triangles)[4]
Without the details inside the zigzag bands the mat is pmg; with the details but without the distinction between brown and black it is pgg.
Ignoring the wavy borders of the tiles, the pavement is pgg.
Group cm
-
Computer generated -
Dress of Amun, from Abu Simbel, Egypt -
Dado from Biban el Moluk, Egypt -
Indian metalwork at the Great Exhibition in 1851 -
Dress of a figure in a tomb at Biban el Moluk, Egypt
Group pmm
-
Computer generated -
Mummy case stored in The Louvre -
Mummy case stored in The Louvre. Would be type p4m except for the mismatched coloring. -
Compact packing of two sizes of circle. -
Another compact packing of two sizes of circle. -
Another compact packing of two sizes of circle.
Group pmg
-
Computer generated -
Cloth, Sandwich Islands (Hawaii) -
Floor tiling in Prague, the Czech Republic -
Bowl from Kerma -
Pentagon packing
Group pgg
-
Computer generated
Group cmm
-
Computer generated -
one of the 8 semi-regular tessellations; ignoring color this is this group cmm, otherwise group p1 -
Turkish dish
Group p4
A p4 pattern can be looked upon as a repetition in rows and columns of equal square tiles with 4-fold rotational symmetry. Also it can be looked upon as a checkerboard pattern of two such tiles, a factor smaller and rotated 45°.
-
Computer generated -
Viennese cane -
Renaissance earthenware
Group p4m
Examples displayed with the smallest translations horizontal and vertical (like in the diagram):
-
Computer generated -
one of the 3 regular tessellations (in this checkerboard coloring, smallest translations are diagonal) -
Demiregular tiling with triangles; ignoring colors, this is p4m, otherwise cmm -
one of the 8 semi-regular tessellations (ignoring color also, with smaller translations) -
Compact packing of two sizes of circle.
Examples displayed with the smallest translations diagonal (like on a checkerboard):
-
Cathedral of Bourges
Group p4g
-
Computer generated -
Fly screen, U.S. -
Painting, China -
one of the colorings of the snub square tiling (see also at pg)
Group p3
-
Computer generated -
one of the 8 semi-regular tessellations (ignoring the colors: p6); the translation vectors are rotated a little to the right compared with the directions in the underlying hexagonal lattice of the image -
Wall tiling in the Alhambra, Spain (and the whole wall); ignoring all colors this is p3 (ignoring only star colors it is p1)
Group p3m1
-
one of the 3 regular tessellations (ignoring colors: p6m) -
another regular tessellation (ignoring colors: p6m) -
one of the 8 semi-regular tessellations (ignoring colors: p6m) -
Persian ornament -
Painting, China (see detailed image) -
Computer generated -
Compact packing of two sizes of circle.
Group p31m
-
Painting, China -
Computer generated
Group p6
-
Computer generated -
Persian ornament
Group p6m
-
Computer generated -
one of the 8 semi-regular tessellations -
another semi-regular tessellation -
another semi-regular tessellation -
Compact packing of two sizes of circle. -
Another compact packing of two sizes of circle.
Lattice types
There are five lattice types, corresponding to the five possible wallpaper groups of the lattice itself. The wallpaper group of a pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself.
- In the 5 cases of rotational symmetry of order 3 or 6, the cell consists of two equilateral triangles (hexagonal lattice, itself p6m).
- In the 3 cases of rotational symmetry of order 4, the cell is a square (square lattice, itself p4m).
- In the 5 cases of reflection or glide reflection, but not both, the cell is a rectangle (rectangular lattice, itself pmm), therefore the diagrams show a rectangle, but a special case is that it actually is a square.
- In the 2 cases of reflection combined with glide reflection, the cell is a rhombus (rhombic lattice, itself cmm); a special case is that it actually is a square.
- In the case of only rotational symmetry of order 2, and the case of no other symmetry than translational, the cell is in general a parallelogram (parallelogrammatic lattice, itself p2), therefore the diagrams show a parallelogram, but special cases are that it actually is a rectangle, rhombus, or square.
Symmetry groups
The actual symmetry group should be distinguished from the wallpaper group. Wallpaper groups are collections of symmetry groups. There are 17 of these collections, but for each collection there are infinitely many symmetry groups, in the sense of actual groups of isometries. These depend, apart from the wallpaper group, on a number of parameters for the translation vectors, the orientation and position of the reflection axes and rotation centers.
The numbers of degrees of freedom are:
- 6 for p2
- 5 for pmm, pmg, pgg, and cmm
- 4 for the rest.
However, within each wallpaper group, all symmetry groups are algebraically isomorphic.
Some symmetry group isomorphisms:
- p1: Z2
- pm: Z × D∞
- pmm: D∞ × D∞.
Dependence of wallpaper groups on transformations
- The wallpaper group of a pattern is invariant under isometries and uniform scaling (similarity transformations).
- Translational symmetry is preserved under arbitrary bijective affine transformations.
- Rotational symmetry of order two ditto; this means also that 4- and 6-fold rotation centres at least keep 2-fold rotational symmetry.
- Reflection in a line and glide reflection are preserved on expansion/contraction along, or perpendicular to, the axis of reflection and glide reflection. It changes p6m, p4g, and p3m1 into cmm, p3m1 into cm, and p4m, depending on direction of expansion/contraction, into pmm or cmm. A pattern of symmetrically staggered rows of points is special in that it can convert by expansion/contraction from p6m to p4m.
Note that when a transformation decreases symmetry, a transformation of the same kind (the inverse) obviously for some patterns increases the symmetry. Such a special property of a pattern (e.g. expansion in one direction produces a pattern with 4-fold symmetry) is not counted as a form of extra symmetry.
Change of colors does not affect the wallpaper group if any two points that have the same color before the change, also have the same color after the change, and any two points that have different colors before the change, also have different colors after the change.
If the former applies, but not the latter, such as when converting a color image to one in black and white, then symmetries are preserved, but they may increase, so that the wallpaper group can change.
Web demo and software
There exist several software graphic tools that will let you create 2D patterns using wallpaper symmetry groups. Usually, you can edit the original tile and its copies in the entire pattern are updated automatically.
- MadPattern, a free set of Adobe Illustrator templates that support the 17 wallpaper groups
- Tess, a nagware tessellation program for multiple platforms, supports all wallpaper, frieze, and rosette groups, as well as Heesch tilings.
- Kali, online graphical symmetry editor applet.
- Kali, free downloadable Kali for Windows and Mac Classic.
- Inkscape, a free vector graphics editor, supports all 17 groups plus arbitrary scales, shifts, rotates, and color changes per row or per column, optionally randomized to a given degree. (See [1])
- SymmetryWorks is a commercial plugin for Adobe Illustrator, supports all 17 groups.
- Arabeske is a free standalone tool, supports a subset of wallpaper groups.
See also
- List of planar symmetry groups (summary of this page)
- Tessellation
- Point group
- Crystallography
- Symmetry groups in one dimension
- M. C. Escher
- Aperiodic tiling
Notes
- ^ E. Fedorov (1891) "Simmetrija na ploskosti" [Symmetry in the plane], Zapiski Imperatorskogo Sant-Petersburgskogo Mineralogicheskogo Obshchestva [Proceedings of the Imperial St. Petersburg Mineralogical Society], series 2, vol. 28, pages 345-291 (in Russian).
- ^ George Pólya (1924) "Über die Analogie der Kristallsymmetrie in der Ebene," Zeitschrift für Kristallographie, vol. 60, pages 278–282.
- ^ Weyl, Hermann (1952), Symmetry, Princeton University Press, ISBN 0-691-02374-3
- ^ It helps to consider the squares as the background, then we see a simple patterns of rows of rhombuses.
References
- The Grammar of Ornament (1856), by Owen Jones. Many of the images in this article are from this book; it contains many more.
- J. H. Conway (1992). "The Orbifold Notation for Surface Groups". In: M. W. Liebeck and J. Saxl (eds.), Groups, Combinatorics and Geometry, Proceedings of the L.M.S. Durham Symposium, July 5–15, Durham, UK, 1990; London Math. Soc. Lecture Notes Series 165. Cambridge University Press, Cambridge. pp. 438–447
- Grünbaum, Branko; Shephard, G. C. (1987): Tilings and Patterns. New York: Freeman. ISBN 0-7167-1193-1.
- Pattern Design, Lewis F. Day
External links
- The 17 plane symmetry groups by David E. Joyce
- Introduction to wallpaper patterns by Chaim Goodman-Strauss and Heidi Burgiel
- Description by Silvio Levy
- Example tiling for each group, with dynamic demos of properties
- Overview with example tiling for each group
- Tiling plane and fancy by Steve Edwards
- Escher Web Sketch, a java applet with interactive tools for drawing in all 17 plane symmetry groups
- Burak, a Java applet for drawing symmetry groups.
- Beobachtungen zum geometrischen Motiv der Pelta
- Seventeen Kinds of Wallpaper Patterns the 17 symmetries found in traditional Japanese patterns.
- Math on the Walls- Natalie Wolchover





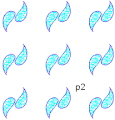










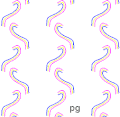



![One of the colorings of the snub square tiling; the glide reflection lines are in the direction upper left / lower right; ignoring colors there is much more symmetry than just pg, then it is p4g (see there for this image with equally colored triangles)[4]](/upwiki/wikipedia/commons/thumb/c/c3/Tile_33434.svg/120px-Tile_33434.svg.png)