Wikipedia:Reference desk/Mathematics

Welcome to the mathematics section
of the Wikipedia reference desk.

skip to bottom

Select a section:

• Computing
• Entertainment
• Humanities
• Language
• Mathematics
• Science
• Miscellaneous
• Archives

Want a faster answer?

Main page: Help searching Wikipedia

   

How can I get my question answered?

• Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
• Post your question to only one section, providing a short header that gives the topic of your question.
• Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
• Don't post personal contact information – it will be removed. Any answers will be provided here.
• Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
• Note:
  • We don't answer (and may remove) questions that require medical diagnosis or legal advice.
  • We don't answer requests for opinions, predictions or debate.
  • We don't do your homework for you, though we'll help you past the stuck point.
  • We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.

Ready? Ask a new question!

How do I answer a question?

Main page: Wikipedia:Reference desk/Guidelines

• The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.

See also:

• Teahouse
• Help desk
• Village pump
• Help manual

May 10

Transcendental Functions

Why are trigonometric functions transcendental? Besides a formal proof, is there some intutition behind the reason? Thanks-Shahab (talk) 01:54, 10 May 2011 (UTC)

I think maybe the intuition is, why should they be algebraic? Being an algebraic function is a very special thing. If there's no reason you can elucidate that a function should be algebraic, then it's probably not. --Trovatore (talk) 02:01, 10 May 2011 (UTC)

It all boils down to why is π transcendental. Trigonometric functions of a rational number times π are algebraic. Dmcq (talk) 08:45, 10 May 2011 (UTC)

Dmcq - not sure if I understand you correctly. Are you saying that $\sin(x)$ is a transcendental function but $\sin(\pi x)$ is an algebraic function ? So we can transform a transcendental function into an algebraic function or vice versa by rescaling the x axis ?? Gandalf61 (talk) 09:18, 10 May 2011 (UTC)

I took him to mean that the value of a trig function at a rational multiple of $\pi$ was algebraic as a number. Icthyos (talk) 09:51, 10 May 2011 (UTC)

Yes exactly, the function itself can't be transformed that way into an algebraic one, for one thing sin has an infinity of zeroes. Dmcq (talk) 11:57, 10 May 2011 (UTC)

I think a trigonometric function grows too fast (exponentially) for an algebraic function. – b_jonas 14:22, 10 May 2011 (UTC)

Presumably you mean in the imaginary axis? --COVIZAPIBETEFOKY (talk) 17:27, 10 May 2011 (UTC)

Well, it doesn't grow exponentially on the real axis, does it? But to stay in real numbers, I think it's also true that a nonconstant algebraic function cannot be periodic. -- Meni Rosenfeld (talk) 10:31, 11 May 2011 (UTC)

An algebraic function having a taylor expansion which is convergent for all values of x, is a polynomial. The functions e^x and sin(x) has taylor expansions which are convergent for all values of x, but they are not polynomials. So e^x and sin(x) are transcendental functions. This is my intuitive reason. Bo Jacoby (talk) 21:13, 10 May 2011 (UTC).

Thank you all. My purpose was to find out an intuitive reason to explain the meaning of a transcendental function to someone who barely knows calculus. Maybe, I can explain a transcendental function as follows: All the nice functions are made up of sums of powers of x. (This is true for the complex case certainly as analytic functions are precisely the true functions of z, but I cannot tell that). So all the nice functions that we have are polynomials or sort of "infinite polynomials". In the former case they are called algebraic (for obvious reasons) and in the latter since they go beyond finite sums and products they are called transcendental (the non-nice ones are also put in this category since they too transcend algebra). Trigonometric functions fall in the latter category. However is there some intuitive way to relate the Taylor expansions of the sine with the y-coordinates of the unit circle? Preferably without using any calculus?-Shahab (talk) 09:18, 11 May 2011 (UTC)

I'd say this gives the wrong impression of what an algebraic function is. If you want to say that sin x is not a polynomial just say so. But ${\sqrt {x^{2}+1}}$ is algebraic and it doesn't have a finite power series. -- Meni Rosenfeld (talk) 10:31, 11 May 2011 (UTC)

Forgive my ignorance but I based my understanding on the remark "An algebraic function having a taylor expansion which is convergent for all values of x, is a polynomial." above. Maybe I need to understand things properly yet-Shahab (talk) 17:37, 11 May 2011 (UTC)

Well, that's not a contradiction. The power series for ${\sqrt {x^{2}+1}}$, near (say) x=0, has a radius of convergence of 1; you can tell because it can't work at x=i, where the function has a branch point. So even on the real line, the series diverges for x greater than 1 or less than −1. You can get series with larger radii of convergence by taking a different center, but the radius will always be finite. --Trovatore (talk) 19:14, 11 May 2011 (UTC)

Kelly criterion vs logarithmic utility function

Can someone please explain to me why, assuming we have a bankroll of 1 and are betting x, the Kelly fraction f is also the maximum of the expected utility calculated using logarithmic utility. i.e. if we're betting x with a win probability of p, our expected value (EV) is

EV = (1+x)*p + (1-x)*(1-p)

while our expected utility (u) is

log(u) = log [(1+x)^p] + log [(1-x)^(1-p)]
log(u) = p log (1+x) + (1-p) log (1-x)
u = (1+x)^p * (1-x)^(1-p)

Why is this particular utility function the best one in maximizing long-term profits over a series of fractional bets? Thank you. 161.53.179.232 (talk) 11:34, 10 May 2011 (UTC)

Well it's only best if you don't have a spread of bets, this is one of the reasons people have a spread of shares - they do better than this. Try thinking about the log of the amount, it will go up or down by a constant amount and your intuition would be correct about the utility of the logs. Dmcq (talk) 12:04, 10 May 2011 (UTC)

You have some problems with your notation. If we denote our bankroll by $r$, then our utility is $u=\log r$ and we have

E[r] = r_0*[(1+x)*p + (1-x)*(1-p)]
E[u] = u_0 + p log (1+x) + (1-p) log (1-x)

Now, a utility function cannot be "best for" anything. A utility function is primary and embodies the desires of an individual - optimization comes after the function was decided. If an individual's utility function is linear in his bankroll then he should go for broke on every bet, but that's not realistic because of the diminishing marginal returns of money. A logarithmic function embodies the assumption that a person who has $10,000 is as happy about getting $100 as a person who has $100,000 is about getting $1,000. If that's the utility function used, you can observe that the final utility is the sum of independent random variables, one for each bet (assuming the fraction wagered is chosen independently of previous wins), so the central limit theorem kicks in. -- Meni Rosenfeld (talk) 10:08, 11 May 2011 (UTC)

Very sorry I misread the question. In fact I'd worked the Kelly criterion myself years ago so I should have known better, but I didn't known it was called that and just assumed the question was about volatility in shares. I've been meaning to have a good read of Black–Scholes even if it did lead to a financial collapse and see what all this area is like nowadays. Dmcq (talk) 14:56, 11 May 2011 (UTC)

May 11

Using part of a character table to calculate the size of conjugacy classes

Hello all,

I have the following 5 rows of a 'mystery' group with 7 cclasses:

1  1  1  1  1  1  1
1  1  1  1 -1 -1 -1
4  0  1 -1  2 -1  0
4  0  1 -1 -2  1  0
5  1 -1  0  1  1 -1

and I have been asked to calculate the size of each conjugacy class and the remaining 2 rows of the table. I am not allowed to identify the table with a specific group unless I can justify it.

Now, we can easily get another character as the product of the second and fifth rows of the table, leaving 1 final character. I do not know the order of the group. I am aware that the sum of the degrees squared equals the order of the group, and that the columns are orthogonal in the normal sense and the rows are orthonormal in the character inner product. I also know that the dot product of a column with itself gives us the size of the centralizer of an element in that conjugacy class (i.e. |G| over the size of the conj class), but since we don't have the final row, I can't seem to use the column orthogonality, and since we don't have any full columns or cclass sizes, I can't use row orthonormality, unless I want to obtain lots of linear equations in 7 variables to solve. Can anyone suggest a better, not-too-complicated way to finish the table and find the size of the conjugacy classes? (Not necessarily in that order - it seems like whichever way I do it one will follow easily from the other.)

Thanks! Otherlobby17 (talk) 01:38, 11 May 2011 (UTC)

Let G be the order of the group and G1, G2, ... G7 be the order of the conjugacy classes. Taking the sum of squares of characters in row 1 and 5, G1 + G2 + G3 + G4 + G5 + G6 + G7=G and 25G1 + G2 + G3 + G5 + G6 + G7=G. Subtracting gives G4=24. For the last character you get the values in columns 3, 5, 6, 7 are 0 due to orthogonality of columns. From these you get G3=G/6, G5=G/12, G6=G/6, G7=G/4. Use this to compute the orthogonality of row 1 and row 3 and solve for G to get G=120. Once you get this the rest of the table should be straightforward. --RDBury (talk) 03:15, 11 May 2011 (UTC)

You ment to write G4=24G1. Bo Jacoby (talk) 06:15, 11 May 2011 (UTC).

Actually no, the conjugacy class for the first column is the identity element, so it has 1 element. I did mean to write that out though.--RDBury (talk) 10:29, 11 May 2011 (UTC)

So you say that G1=1 ? Bo Jacoby (talk) 12:55, 11 May 2011 (UTC).

I see, thankyou! Yes, G1 is 1, that was the obvious fact I was overlooking as it happens. Thanks :) Otherlobby17 (talk) 15:56, 11 May 2011 (UTC)

should gay couples be given the legal right as heterosexual in adopting children?

Discussion closed: off topic for this desk
The following discussion has been closed. Please do not modify it.
should gay couples be given the legal right as heterosexual in adopting children? am strongly against.. —Preceding unsigned comment added by Lizz4sunday (talk • contribs) 06:27, 11 May 2011 (UTC) Why on Earth is this on the Math Desk ? On the theory that 1 + 1 = 3 ? It's probably not appropriate anywhere on the Ref Desk, though, since it's a request for opinions rather than facts. StuRat (talk) 06:37, 11 May 2011 (UTC) For what it's worth, Wikipedia has an article on LGBT adoption. If you want a political discussion, you should visit a forum. 130.88.134.222 (talk) 08:52, 11 May 2011 (UTC) Not sure what some of those terms mean. Is couple used in the sense of a tuple with two members or as a system of forces producing a moment? What do the terms gay and heterosexual mean? The 'adopting children' sounds more like computing to me. :) Dmcq (talk) 09:54, 11 May 2011 (UTC) By "couple" he means an electric dipole. "Gay" is a configuration dominated by gravitational forces, "heterosexual" one dominated by electrostatic forces. "Legal right" is referring to the right-hand law. This question should be in the science desk. -- Meni Rosenfeld (talk) 10:12, 11 May 2011 (UTC)

Markov chain mapping tools

Assume that I have a file that describes a Markov chain. I can format it in any way necessary. Are there any standard tools for mapping or graphing the Markov chain in an image file? I have done many small ones by hand, but I have some chains with about 5,000 states that I want to map just to demonstrate that they are mostly disjoint. -- kainaw™ 12:29, 11 May 2011 (UTC)

Right now, I'm using graphviz. I have been waiting on one graph for about 4 hours and there is no sign it will be produced anytime soon. Perhaps I need to look into tricks for making graphviz run faster. -- kainaw™ 15:24, 11 May 2011 (UTC)

It seems like you're looking for Markov clusterings. Take a look at that link. It gives "a fast and scalable unsupervised cluster algorithm for networks (also known as graphs) based on simulation of (stochastic) flow in graphs." That algorithm will pick out the network clusters, i.e. sets of vertices with higher than average mutual edge connections. I hope that helps. — Fly by Night (talk) 23:34, 11 May 2011 (UTC)

Thanks. I killed the graphviz process after letting it run for 24 hours on a single chain. Hopefully this works better. -- kainaw™ 12:08, 12 May 2011 (UTC)

Another representation theory question: misunderstanding of the way irreducible representations decompose

Hello everyone, I think I'm misunderstanding something in representation theory and I was hoping you could explain: I've scoured the internet but couldn't find anything relevant.

I've just proved that if G is a finite group with centre Z, then if G has a complex irreducible representation which is faithful, then Z is cyclic. However, I'm now trying to show a partial converse: the rest of the problem I am stuck on is this:

"Now assume the order of G is a power of the prime p, and Z is cyclic. If $\rho$ is a faithful representation of G, show that some irreducible component of $\rho$ is faithful. You may use without fact the proof that since G is a p-group, Z is non-trivial and any non-trivial normal subgroup of G intersects Z non-trivially."

Now I believe since we're working over $\mathbb {C}$ with finite groups and representations, we can always decompose $\rho$ as a direct sum $\oplus _{i}\rho _{i}$ of irreducible representations, each of which combines to create a sort of 'block diagonal' action $\rho$ on the various G-invariant subspaces of the vector space V on which our group acts - I think this follows from Maschke's theorem but I may be misunderstanding the way a finite dimensional representation of a finite group over a field of characteristic 0 is 'reducible'. However, this clearly can not be the case, as if the action was just 'block diagonal' with zeros in the off-diagonal blocks, then clearly every representation $\rho _{i}$ has a very much non-trivial kernel, so none of these are faithful.

What am I misunderstanding? The question seems to be intending to lead me in a very specific direction but I don't think I'll be able to appreciate it until I grasp what I am misunderstanding about the problem and what I should be thinking instead. Help welcomed and appreciated! Many thanks as always :) Otherlobby17 (talk) 17:41, 11 May 2011 (UTC)

Not sure where you're getting "every representation $\rho _{i}$ has a very much non-trivial kernel, so none of these are faithful." Each block is an irreducible representation which may or may not be faithful.--RDBury (talk) 20:23, 11 May 2011 (UTC)

Any normal group intersects Z basically says if a representation is faithful on Z then it is faithful on G. I don't have a solution to the stated problem off the top of my head but I'm convinced that you should be looking at the eigenspace decomposition as well, particularly the eigenspace decomposition of the generator of Z.--RDBury (talk) 20:44, 11 May 2011 (UTC)

I see the bit that I missed now. Look at the eigenvalues of a generator of Z in ρ. Let Z have order pⁿ. If none of the eigenvalues has order pⁿ (in C) then they all have order dividing pⁿ⁻¹ and that means ρ isn't faithful on Z much less G. So one of the eigenvalues has order pⁿ. In the decomposition of ρ into ρ_i the eigenvalues don't change, they just get rearranged into groups. So the eigenvalue we're interested in must be an eigenvalue of one of the ρ_i. This ρ_i is then faithful on Z and therefore faithful on G.--RDBury (talk) 21:24, 11 May 2011 (UTC)

That's brilliant: god only knows how long it would have taken me to figure that out myself! Looks like I need more practice. I think my mistake above was thinking mistakenly that the $\rho _{i}$ are giving a representation on the entire space V on which our G acts, but looking at it as a block matrix for $\rho (g)$ we would have that all but a small number of columns for that $\rho _{i}(g)$ 'block' within the bigger matrix for would be zero within the rows corresponding to that block, and therefore the $\rho _{i}$ would take almost everything except for a small number of columns to zero: in fact, I suppose what we're really saying is that $\rho _{i}(g)$ is only mapping onto a smaller-dimension space in the first place, so those zero parts in the matrix of $\rho (g)$ aren't really corresponding to part of the subrepresentation. I don't know if that made any sense but it is clearer in my head so thankyou!

I greatly appreciate you helping me out, you've alleviated a lot of my confusion! Thanks :-) Otherlobby17 (talk) 12:07, 12 May 2011 (UTC)

Probability problem.

Hi.I have a question about probability.

Imagine we drop a coin 100 times. the probability for each side is 1/2 so each side must be shown 50 times. now, if one side comes 51 times and the other 49 times; which conclusion is correct:

1.the probabilty doesn't tell us exactly how many times each side comes.

2.the conditions in which the experiment is done led to this result (for example the area of the coin is a little more on one side)

3.none of above

thanks. —Preceding unsigned comment added by Irrational number (talk • contribs) 18:56, 11 May 2011 (UTC)

The probability is 1/2 (or 50%) per drop. It is not "50% of the time you will get heads and 50% of the time you will get tails." -- kainaw™ 19:00, 11 May 2011 (UTC)

If you are surprised by this result, then you should conclude that you do not yet understand probability, and need to study it more if you wish to gain a stronger understanding. --COVIZAPIBETEFOKY (talk) 19:13, 11 May 2011 (UTC)

Since they didn't say it, the answer is #1. The probability being 1/2 doesn't mean you'll get exactly 50 heads and 50 tails out of 100 throws. Staecker (talk) 22:17, 11 May 2011 (UTC)

1. If you toss a coin once it doesn't land half on one side and half on the other, it either lands on one side or the other. Dmcq (talk) 23:36, 11 May 2011 (UTC)

The question reflects a lack of understanding of the law of large numbers, and perhaps the best way to gain an understanding would be to read that article (or at least the first part of it; the later parts are technical). Looie496 (talk) 02:02, 12 May 2011 (UTC)

• Also, the probability is 50-50 for a fair coin, but most coins are NOT fair. "Since the images on the two sides of actual coins are made of raised metal, the toss is likely to slightly favor one face or the other if the coin is allowed to roll on one edge upon landing." (see coin toss). --Mgm|^(talk) 08:38, 12 May 2011 (UTC)

There is a saying "Dice have no memory" (the article it links too is maybe too technical for you). If you threw the coin 99 times, and got 49 heads and 50 tails, how can a dumb coin "know" what to get in the last throw? It can't. Regarding the exact number of realizations, statisticians can come up with confidence intervals, in this context it would be for example "if the result is 60 vs. 40 or more skewed, it is more than 95% likely that the probability is not 1/2" (I made up the numbers now but it is straightforward to calculate if you know the method). Jørgen (talk) 10:48, 12 May 2011 (UTC)

If p is the probability of heads, then the probability that p =/= 1/2 is probably 1 whatever results are observed. 86.179.117.4 (talk) 11:29, 12 May 2011 (UTC)

You're right, of course. I should have said "probability is less than 1/2". Or maybe even that's wrong and I didn't think about it enough and should strike everything. Sorry. Jørgen (talk) 14:02, 12 May 2011 (UTC)

This is a classic confusion in statistics. The real question isn't whether or not the actual probability is exactly 1/2, but whether it's close enough to 1/2 for ones purposes. A test of the sort that you describe would conclude that assigning a probability of 1/2 to the coin-toss would result in a bad model of the coin (or the result of the experiment was unusual). --COVIZAPIBETEFOKY (talk) 16:00, 12 May 2011 (UTC)

I find even the calculation of the probability that p is close to 1/2 (say 1/2 - t <= p <= 1/2 + t) a troublesome one. I don't see how to do it without assuming some prior distribution of p (prior to observing the results), which is kind of begging the question. Unless I am missing something...? 86.181.203.129 (talk) 17:30, 12 May 2011 (UTC)

Bayesians use a prior distribution on p, and update on the data to find a posterior. Frequentists say "if p was 1/2, the probability of finding a result as surprising or more would be x". -- Meni Rosenfeld (talk) 06:05, 13 May 2011 (UTC)

From probabilities follow probabilities, not certainties. Assuming that p is 1/2, and getting heads every time out of a hundred times, you can only say that the result is improbable, not impossible. Knowing a population you can say something about a sample. This is called deduction and this is what frequentists do. Knowing a sample you can say something about the population. This is called induction and this is what Bayesians do. Bo Jacoby (talk) 06:47, 13 May 2011 (UTC).

May 12

Special Relativity Small Angle Approx.

Given cosθ =(E-3mc²)/(E+mc²) where E is the relativistic energy, how does one show that for v<<c, θ≈π-v/c? I know that it involves Taylor expansion approximation but couldn't quite get it into this form... Thanks! —Preceding unsigned comment added by 131.111.222.12 (talk) 11:04, 12 May 2011 (UTC)

Let $\alpha =\pi -\theta$ and $r=v/c$. Show that $E=mc^{2}(1+r^{2}/2+O(r^{4}))$ and combine it with $\cos \alpha =-\cos \theta$ to show that this is both $1-\alpha ^{2}/2+O(\alpha ^{4})$ and $1-r^{2}/2+O(r^{4})$. Now, intuitively this should imply that $\alpha =r+O(r^{2})$, but I don't know of an easy rigorous way to show it. -- Meni Rosenfeld (talk) 12:37, 12 May 2011 (UTC)

Thanks, Meni! :) —Preceding unsigned comment added by 131.111.222.12 (talk) 13:10, 12 May 2011 (UTC)

Four Point Particles

Hi, I have a solution to this, but I am looking for a more elegant solution. If we are given 4 positively charged particles at the 4 corners of a square, is there a better proof for the stability of the central point of square for a 5th positively charged particle apart from (the clumsy way of) computing the 2nd partial derivatives of the U(x,y)...? Thanks! —Preceding unsigned comment added by 131.111.222.12 (talk) 12:36, 12 May 2011 (UTC)

You can use symmetry to significantly cut down on the work. That this is an equilibrium (zero partial derivatives) is obvious from symmetry. The ${\frac {}{\partial x\partial y}}$ 2nd derivative is 0 by symmetry, so you only need to show that the ${\frac {}{\partial x\partial x}}$ and ${\frac {}{\partial y\partial y}}$ (which are equal because of symmetry) are positive. When calculating ${\frac {}{\partial x\partial x}}$, the force applied by the particles with the same x but different ys have the same x-component, so you can calculate for just one on the left and one on the right. wlog the corners of the square are at +-1, so the x-component of the force the particles apply is ${\frac {1+x}{((1+x)^{2}+1)^{3/2}}}-{\frac {1-x}{((1-x)^{2}+1)^{3/2}}}$, so you just need to show the derivative of this is negative. In fact, because the second summand is the negated reflection of the first, it has the same derivative at 0 as the first, so it's enough to show that the derivative of ${\frac {1+x}{((1+x)^{2}+1)^{3/2}}}$ is negative, or equivalently, that the derivative of ${\frac {t}{(t^{2}+1)^{3/2}}}$ is negative at $t=1$. So the only actual calculation we have to do is the derivative of that last part. -- Meni Rosenfeld (talk) 12:47, 12 May 2011 (UTC)

Thank you!

Density of a sphere packing

In the article Close-packing of spheres and Sphere packing, the density of these packings is mentioned. Yet it is not clear to me how the density of an arbitrary sphere packing is calculated. How does one calculate this? For example, how do I calculate the density of the hcp and the fcc packing (see also File:Close packing box.svg)? Toshio Yamaguchi (talk) 13:25, 12 May 2011 (UTC)

For repeating patterns, you could find a repeating cell and then calculate the fraction of that cell which is "covered" by the spheres. Since the whole lattice is made up from copies of the repeating cell, the density of the lattice as a whole is the same. 86.181.203.129 (talk) 17:25, 12 May 2011 (UTC)

Note that for some patterns, there will be "edge effects", where the density is lower on the faces. However, for a larger structure with millions of cells, this will be insignificant. StuRat (talk) 18:19, 12 May 2011 (UTC)

What particularly strong reasons are there in favor of using equivalence classes?

I don't doubt the existence of such reasons; they're just not obvious and I feel like the math professors just tell us that this is the way to identify multiple things as being equal, without really justifying it. The way to define integer arithmetic modulo n is to break the integers into n equivalence classes. The alternative is to just compute with integers, with the understanding that certain things are 'equal' according to an equivalence relation. Just as with the equivalence class approach, of course, you would have to show that addition and multiplication are well-behaved wrt the equivalence relation defined on the integers.

One argument for equivalence classes is that you can easily speak of the cardinality of the partition (as in, there are exactly n equivalence classes of integers modulo n), whereas it is more difficult to phrase that same question if you haven't collected the set into equivalence classes. What are some others? One possibility: are there examples of operations or other forms of structure that wouldn't be possible or easy to define without having first collected sets of equivalent elements together? --COVIZAPIBETEFOKY (talk) 14:28, 12 May 2011 (UTC)

There are lots of applications and it's really part of the basic machinery of mathematics in general. One application is the construction of number systems: integers can be defined as equivalence classes of pairs of natural numbers, rationals can be defined as equivalence classes of pairs of integers, reals can be defined as equivalence classes of Cauchy sequences of rationals. Surreal numbers use equivalence classes implicitly. In algebra there are quotient groups, quotient rings, quotient algebras, etc. and in topology there are quotient spaces. There are hundreds of articles that link to our article on them, so I'd say there are really too many examples to list.--RDBury (talk) 17:21, 12 May 2011 (UTC)

I think you missed the point. He's not asking for applications. He's asking for a reason to code the notion into equivalence classes, instead of simply redefining equality and taking care of it at the level of logic.

There are actually lots of problems that show up, at least at a formal level, when you try to make equality be anything other than strict identity. I'm sure people have tried to do that; I'd be interested myself in a pointer to how it goes and what the difficulties are, because I'm not coming up with the details at the moment.

At an informal level, though, it usually is more convenient to work with representatives rather than classes, and just be careful that everything you do with them respects the equivalence relation. So I guess I'd say that in most cases the purpose of equivalence classes is not to help you do the mathematics, but to make it clear how the mathematics would be formalized if you need to. --Trovatore (talk) 17:32, 12 May 2011 (UTC)

If you ask what are the elements of a quotient group, what would the answer be if not equivalence classes? I'm not saying there's no possible answer to that question, but maybe someone should propose one if the wisdom of speaking of equivalence classes is questioned. Michael Hardy (talk) 18:58, 12 May 2011 (UTC)

The answer would be that they're just the elements of the dividend group, except that now you're considering some of them to be the same. --Trovatore (talk) 19:00, 12 May 2011 (UTC)

I'm not questioning the wisdom of equivalence classes. I'm asking for examples where they become an indispensable tool, either in comprehension of a particular concept or in the definitions themselves, rather than merely being a convenient means of description.

I do think this lends itself a good answer to my question, though: if one wants to talk about homomorphisms between groups, such a thing would be much harder to define if you were to allow distinct elements of the set to be considered equivalent.

So, if I may narrow down my question a bit more:

Are there any examples of a set $S$ with an equivalence relation $\sim$, where a map $f:S/\sim \to S/\sim$ is easier to define than a corresponding map $f':S\to S$ inducing the same $f$? It is always easy to define $f$ given a definition for $f'$, but going the other direction would, in general, be trickier, and maybe impossible to do without utilizing the axiom of choice.

To be clear: I'm not asking for an existence result. I'm asking for an explicitly given example of $S,\sim ,f$, where $f$ has a simpler definition than any $f'$ could hope to have. --COVIZAPIBETEFOKY (talk) 03:45, 13 May 2011 (UTC)

I'm not sure that the definition of $f$ is supposed to be simpler than that of $f'$. In fact, often you define a function like $f'$ first and then verify that it is constant on each equivalence class, and so "descends to the quotient". The existence of $f$ tells you that the original function has some structure that may not always be convenient to express explicitly. For instance, consider the quotient $P/L$ of the plane by a one-dimensional subspace. A linear function $f:P/L\to \mathbb {R}$ corresponds to a linear function $f':P\to \mathbb {R}$ that is constant on every line parallel to $L$. Sławomir Biały (talk) 10:30, 13 May 2011 (UTC)

To me, your idea of using elements of S but considering some of them equal is exactly the same as the idea of equivalence classes (but stated informally, and with the details left in the background). It may seem like thinking about the set [s], the equivalence class of s, instead of just thinking about s, is unnecessary baggage; but it really isn't.

As soon as you say you're now considering some elements equal, I'm going to ask you which ones. In particular, which ones are equal to s? You can explain it however you want, but you're defining an equivalence relation. And it has to be reflexive, symmetric, and transitive, or you're speaking nonsense. You recognize the importance of well-definedness, but it's nice to have the details in the open.

You'll also run into some notational trouble if you have different notions of = in the same discussion. For an example of this confusion, working modulo 7, we know that 45+15 = 32, because 45 = 3+6(7) = 3, 15 = 1+2(7) = 1, 32 = 4+4(7) = 4, and 3+1 = 4. Of course, I really mean 45+15 =₂ 32, because 45 =₁ 3+6(7) =₂ 3, 15 =₁ 1+2(7) =₂ 1, 32 =₁ 4+4(7) =₂ 4, and 3+1 =₁ 4, where =₁ is the usual equality in the integers and =₂ is the modulo 7 equivalence relation. Using different symbols for different equivalence relations is fine, but I would prefer using brackets to indicate equivalence classes. Either way, though, you're doing exactly the same thing-- you're working with sets of equivalent elements (whether or not you ever use the word "set") and you have to check the same properties to show it's well-defined. There's no mystery or extra baggage to the notion of equivalence classes; that's just the notation and terminology mathematicians have settled on.71.58.77.50 (talk) 14:21, 13 May 2011 (UTC)

I was always talking about equivalence relations.

I disagree (with "your idea of using elements of S but considering some of them equal is exactly the same as the idea of equivalence classes"); I don't think the notion of an equivalence relation is identical to that of an equivalence class, and there is no immediate reason that you should collect equivalent elements into equivalence classes. I don't know why you confuse the two so easily. I know that a partition induces an equivalence relation and vice-versa, but the use of an equivalence relation does not necessitate the use of equivalence classes, as you seem to want to believe. --COVIZAPIBETEFOKY (talk) 01:07, 14 May 2011 (UTC)

As for your last paragraph, that's exactly my point! As long as you are only speaking of the relationships between individual elements (rather than, say, global questions about the set, such as "how many groups of equivalent elements are there?"), the difference between using an equivalence relation and using equivalence classes is purely one of notation. --COVIZAPIBETEFOKY (talk) 01:20, 14 May 2011 (UTC)

It seems to me that mathematicians get uncomfortable in situations where equivalence classes become infeasible, for no good reason. Case in point: cardinality. Two sets are considered equivalent if they have the same cardinality. You cannot collect these into equivalence classes, because the equivalence classes aren't sets. The most common solution is to pick a choice representative, namely, the smallest ordinal of a given cardinality, and work with those. But why should we bother picking special representatives? Why can't we just discuss cardinality as a feature of a set without giving it a specific representative? --COVIZAPIBETEFOKY (talk) 01:25, 14 May 2011 (UTC)

I don't really know any cases where the function is simpler to define on the classes than on the representatives. Most often it's the other way around. That's how we define reducibility on Borel equivalence relations for example, by talking about the functions on the representatives.

I gave an undergrad colloquium talk at San Jose State a year or so ago talking about some of these things; if you're interested it's called How to have more things by forgetting where you put them --Trovatore (talk) 17:56, 13 May 2011 (UTC)

Thanks for that reference, Trovatore! Quite a fascinating read. --COVIZAPIBETEFOKY (talk) 02:15, 14 May 2011 (UTC)

In the usual argument showing that non-measurable sets exist, can you eliminate the use of equivalence classes? Since you need to appeal to the Axiom of Choice allowing you to pick an element of each of the members of the quotient set, it seems to me that you cannot do that. Count Iblis (talk) 22:12, 13 May 2011 (UTC)

Yes, that does seem to be the case, as far as I can tell. --COVIZAPIBETEFOKY (talk) 01:07, 14 May 2011 (UTC)

Simple puzzle

Hi. A square lattice of side n is made up of n^2 square tiles. The number of tiles around the perimeter is n^2 - (n - 2)^2, or 4n - 4. Can anyone think of an intuitive/visual way to appreciate why, for n = 1, the answer is 0 and not 1? (Note: I am not looking for further mathematical/symbolic justifications. I want to be able to look at a single square and "see" why there are zero squares on its perimeter.) 86.181.203.129 (talk) 17:39, 12 May 2011 (UTC)

Just because you have a formula that says zero doesn't mean it is actually zero. And it most certainly looks like one to me. Dmcq (talk) 17:46, 12 May 2011 (UTC)

Nevertheless, it is strange (in my opinion) that a formula which works perfectly well for all other values of n should fail with n = 1. It is equally hard to think of a plausible formula that gives an answer 1 for n = 1 and correct results for all other values of n. 86.181.203.129 (talk) —Preceding undated comment added 17:53, 12 May 2011 (UTC).

It seems to me that the problem comes down to how you define a "perimeter square". Some possibilities:

1) A square where any portion of that square is on the perimeter. This seems to be the def you are using.

2) A square where any portion of that square is on the perimeter and another portion is not. In other words, you can't have an "outside" if you don't have an "inside". This def seems to match that formula better. StuRat (talk) 17:57, 12 May 2011 (UTC)

Perhaps a better formula would be the total squares (n²) minus the interior squares. The tricky part here is defining the interior squares. (n-2)² is the general formula, but this falls apart when n = 0 or 1. So, the correct formula starts with n², but only subtracts (n-2)² in cases where n-2 ≥ 0. I'm not sure how to write that mathematically. StuRat (talk) 18:15, 12 May 2011 (UTC)

It is typical to write formulas that involve a "choice" like that as piecewise defined functions. You could also achieve the result with an Iverson bracket if you really wanted it to appear as a single formula. (You could probably also hack something together that uses the Heaviside step function or the sign function.) —Bkell (talk) 15:47, 14 May 2011 (UTC)

One could incorporate the cases n=0 and n=1 into the formula for the number of "interior" squares by writing this number as $(n-2)_{+}^{2}$, where $(n-2)_{+}=\max\{0,n-2\}$ is the positive part of n-2. Then a general, and correct, formula for the number of "perimeter" squares would be $n^{2}-(n-2)_{+}^{2}$. Then you would be able to look at the square with n=1 and indeed see that the formula says there is one perimeter square. Nm420 (talk) 17:48, 15 May 2011 (UTC)

Poppit probabilities

There's an online game at Pogo called Poppit. Here are the rules:

1) You start with a 2 dimensional array of balloons, 15 wide and 10 high, for 150 balloons total.

2) These balloons are of random color, from a small number of colors. I'm not quite sure what the range of the number of colors is, but 5 seems typical.

3) When two or more balloons of the same color are adjacent, you may pop the group.

4) When a group is popped, any balloons below an empty space float to the top.

5) If any empty column is formed, the balloons on either side float together, as a group, to close the balloons together. Thus, the balloons always form a single contiguous group.

6) The object is to pop all the balloons.

Now for my questions:

A) How many "games" are possible. That is, how many different ways can the balloons be popped ? In the worst possible case, with only groups of 2 formed, there could be up to 150/2 or 75 groups. This means 75 possible pops the first time, then 74, etc. So, I get 75! games. However, does that logic still apply if groups are forming and dissolving based on which previous groups were popped ?

B) Instead of the worst case, what's the average number of games ?

C) To solve the puzzle, and get a perfect game with no balloons left (assuming one is possible), how many possible pops must be considered, on average ? Note that there may be many possible perfect games (orders in which the balloons can be popped to leave none), for any initial arrangement.

My motivation is to write a program to solve Poppit games. (I've already done so for the much smaller (4×4 - 7×7) versions in Pop Fu.) However, my initial assessment is that there are just too many combos to take the brute force approach, as I did with the smaller boards. Am I correct ? What other approach might work ? StuRat (talk) 18:46, 12 May 2011 (UTC)

For searchability, this game is called SameGame. – b_jonas 19:33, 12 May 2011 (UTC)

In A, when you ask "how many different ways can the balloons be popped?", I guess you mean how many different ways can all the balloons be cleared for a given starting grid? (When I first read it, I thought you meant over all possible grids.) What constitutes a "different way"? Suppose all the balloons are initially numbered so they can be uniquely identified as the game progresses. Are games identical only if balloons are popped in the same numerical sequence and they are in the same grid position when popped? 86.181.203.129 (talk) 20:11, 12 May 2011 (UTC)

Yes. StuRat (talk) 20:18, 12 May 2011 (UTC)

Clearly I'm missing something here; I don't even see how you get 75 to begin the 75! calculation. I see 14 * 10 horizontal groups of two, and 15 * 9 vertical groups of two, so the first two balloons can be popped in 275 ways. 86.181.203.129 (talk) 22:14, 12 May 2011 (UTC)

I don't understand. Can you show me what you mean ? Perhaps you're missing that all vertically or horizontally (but not diagonally) connected balloons in a group always pop whenever you pick one. StuRat (talk) 01:02, 13 May 2011 (UTC)

Here's one possible "worst case" configuration, with 75 groups (I used spaces and blank lines to show the groups, they aren't really there):

Y G R B P  Y G R B P  Y G R B P  
Y G R B P  Y G R B P  Y G R B P  

G R B P Y  G R B P Y  G R B P Y  
G R B P Y  G R B P Y  G R B P Y  

Y G R B P  Y G R B P  Y G R B P  
Y G R B P  Y G R B P  Y G R B P  

G R B P Y  G R B P Y  G R B P Y  
G R B P Y  G R B P Y  G R B P Y  

Y G R B P  Y G R B P  Y G R B P  
Y G R B P  Y G R B P  Y G R B P

The colors used are Yellow, Green, Red, Blue and Purple. So, any of the 75 groups could be popped first, leaving 74 groups. Any of those could then be popped, leaving 73 groups, etc. StuRat (talk) 01:02, 13 May 2011 (UTC)

Sorry, ignore me. When I first read your question "How many 'games' are possible" I thought you meant total number of games across all starting grids. Although this was later corrected, I somehow carried on thinking that was the question. If you allow any starting grid, then a pair of poppable balloons can be in any of 275 positions, but that isn't what you're asking. Apologies for the confusion. 86.181.203.129 (talk) 01:32, 13 May 2011 (UTC)

OK, thanks. StuRat (talk) 03:34, 13 May 2011 (UTC)

Some (possibly banal) suggestions for optimizing the program:

• Compute and keep in memory as large an endgame tablebase as possible.
• Try to come up with some easy to calculate heuristic which provides some information on the plausibility of a solution existing (eg, the proportion of adjacent balloon pairs which are of the same color). You can calibrate it by running simulations with number of pieces slightly above what you have in your endgame table. Then use this as a proxy for the optimal move when you can't brute-force deep enough.
• Use a transposition table.
• I don't know if pruning methods like alpha-beta apply for one-player games, but they might be worth thinking about.

-- Meni Rosenfeld (talk) 09:23, 15 May 2011 (UTC)

Some interesting suggestions. I might try the endgame tablebase. I really want to find the best possible solution, though, and using heuristics isn't guaranteed to do that. Then again, what I want may not be possible. StuRat (talk) 04:25, 16 May 2011 (UTC)

May 13

Factoring Polynomials

Err, can someone explain to me how to factor polynomials? I can totally do x^2+bx+c but all of the sudden when I get ax^2+bx+c I just panic and resort to using the quadratic formula. I know there's a faster way to do it, but googling just gives me a whole bunch of stuff I don't understand. Can someone explain a method that's easy to understand?? Thanks! —Preceding unsigned comment added by 142.132.70.60 (talk) 19:21, 13 May 2011 (UTC)

You can factorize the expression by taking out the 'a' and get $ax^{2}+bx+c=a\left(x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}\right)$. Then you can use your techniques on the term inside the big brackets; but don't forget to put the 'a' back in! HTH, Robinh (talk) 20:53, 13 May 2011 (UTC)

Personally, I find you have to start with the "x" term in each, for example (x _ _)(3x _ _), if you can fix the signs (if b>0, and c>0, then both signs are positive, if c>0 and b<0, both are negative) and then see if you can get it from there. If there are only a few possible combinations as factors of c then it's possible to write it out. (Also - a small hint, if you can get it in somewhere: if the brackets start with and even number of xs, then the second part of the bracket must be odd, else the whole thing would divide by two and from inspection is can't (unless you missed that originally)) Grandiose (me, talk, contribs) 21:19, 13 May 2011 (UTC)

$ax^{2}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right)$

The fast way is http://www.wolframalpha.com/input/?i=ax^2%2Bbx%2Bc

The easy-to-understand way is to check that $a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right)$ is equal to $ax^{2}+bx+c$ Bo Jacoby (talk) 11:35, 15 May 2011 (UTC).

Latex

Can someone tell me how to draw the following in latex: a hollow square with a diagonal line going from bottom left corner to top right corner, and each line has an arrow head in the middle (not on the ends), so I want the lines to look like their pointing in some direction but I don't want the arrow head on the end points. I need the diagonal line's arrow head pointing 45 degrees clockwise from north. I also need the four vertices labelled as v. If you could post the code I'd appreciate it. Money is tight (talk) 22:32, 13 May 2011 (UTC)

By far the easiest thing to do is to draw the image in another program, and save it as a .png or .eps or whatever, and use \includegraphics{file}. Invrnc (talk) 23:05, 13 May 2011 (UTC)

You might try Inkscape to produce a .SVG. SVG is based on XML so if the drawing is simple and you're patient and willing to learn the syntax it's possible to create the file with a text editor.--RDBury (talk) 23:35, 13 May 2011 (UTC)

Alternatively, there are lots of packages for coding drawings in latex. PGF/TikZ is very good and has an extensive manual with lots of examples (linked from the article). In fact, the standard picture environment is probably enough for what you want to do - there is a nice Wikibooks article with lots of information about picture, that also discusses xy, tikz, xfig, and others. 81.98.38.48 (talk) 14:47, 14 May 2011 (UTC)

Also, in which direction are the other four arrowheads facing? – b_jonas 06:53, 15 May 2011 (UTC)

The left and right sides of the square are facing upwards, and the top and bottom sides of the square are facing right. Basically I'm trying to draw the triangulation of the torus. Money is tight (talk) 18:54, 15 May 2011 (UTC)

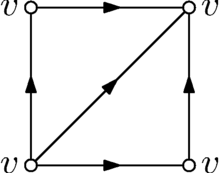
Here's an example (see thumbnail). See its description page for the EPS (encapsulated Postscript) formatted original that has infinite resolution and you can easily use in a LaTeX article.

I don't quite understand why you'd want an arrowhead on the diagonal if this is supposed to show the triangulation of the torus. I thought the arrowheads would mean identifying two edges on the drawing. Anyway, for this image I stick to your description so I've put an arrowhead to the diagonal as well, but feel free to modify it in any way you like (including changing the dimensions, font, etc). – b_jonas 21:50, 15 May 2011 (UTC)

Ah, I get it now. The four vertices are identified, so they should have the same label. I changed the image to have the same label (v) at each vertex. (Still don't get the arrow at the middle.) – b_jonas 21:57, 15 May 2011 (UTC)

Which are Martingales?

I know that there are two criteria for some $M_{t}$ to be an ${\mathcal {F}}_{t}$-Martingale.

Firstly $\mathbb {E} (|M_{t}|)<\infty$.

Secondly $\mathbb {E} (M_{t}|{\mathcal {F}}_{s})=M_{s}$.

Now $W_{t}$ is a Wiener process that generates a filtration ${\mathcal {F}}_{t}$.

I need to determine whether a couple of functions of $W_{t}$ are ${\mathcal {F}}_{t}$-Martingales or not.

The first one is $M_{t}=W_{t}^{2}$.

I'm assuming that this passes the first test. Because $Var(W_{t})=\mathbb {E} (W_{t}^{2})-(\mathbb {E} (W_{t}))^{2}=\mathbb {E} (W_{t}^{2})=\mathbb {E} (|W_{t}^{2}|)=t<\infty$

As for the second test, I'm guessing that it fails, since $\mathbb {E} (W_{t}^{2}|{\mathcal {F}}_{t})=\mathbb {E} (W_{t}^{2}-W_{s}^{2}+W_{s}^{2}|{\mathcal {F}}_{t})=\mathbb {E} (W_{t}^{2}-W_{s}^{2}|{\mathcal {F}}_{t})+W_{s}^{2}=(t-s)+M_{s}\neq M_{s}$

But the second one is much more difficult:

$M_{t}=tW_{t}-\int _{0}^{t}W_{s}ds$

I thought maybe $\mathbb {E} (|M_{t}|)=t\mathbb {E} (W_{t})-\int _{0}^{t}\mathbb {E} (W_{s})ds=0$

But I'm guessing there's something wrong about that. As for checking the second condition I really don't know where to begin. Thorstein90 (talk) 00:54, 14 May 2011 (UTC)

So, the first is not a martingale since it's expectation value is the variance of the Wiener process, which increases with time. The second is a martingale. The condition on the variance is straightforward:

$\operatorname {var} (M_{t})\leq E(M_{t}^{2})=t^{2}\operatorname {var} (W_{t})+2t\int _{0}^{t}E(W_{t}W_{s})ds+\int _{0}^{t}\int _{0}^{t}E(W_{s}W_{s'})\,ds\,ds'$

which you can estimate from above by the Cauchy-Schwarz inequality. For the martingale property, your calculation is basically right, except you need to condition on the initial information ${\mathcal {F}}_{s}$. Then

${\begin{aligned}E(M_{t}|{\mathcal {F}}_{s})&=tW_{s}-\int _{0}^{s}E(W_{s'}|{\mathcal {F}}_{s})\,ds'-\int _{s}^{t}E(W_{s'}|{\mathcal {F}}_{s})\,ds'\\&=tW_{s}-\int _{0}^{s}W_{s'}\,ds'-(t-s)W_{s}=M_{s}.\end{aligned}}$

-Sławomir Biały (talk) 12:20, 16 May 2011 (UTC)

Riemann Hurwitz formula and analytic maps on the Riemann Sphere

Hello everyone, I'm stuck on the following problem and have no idea how to get going on it, was hoping you could help.

Suppose $f:\mathbb {C} _{\infty }\to \mathbb {C} _{\infty }$ is an analytic map of degree 2: show that there exist Mobius transformations S, T such that $SfT:\mathbb {C} _{\infty }\to \mathbb {C} _{\infty }$ is the square map, $v\to v^{2}$.

Now I've just previous to this stated the Riemann Hurwitz formula which applies to f here, and I have also shown that the analytic isomorphisms of the Riemann sphere to itself are the non-constant mobius maps. So, I feel like I must be almost all the way there already, I just need help piecing this together to get the result: any thoughts anyone? Thank you! Totenines99 (talk) 23:59, 13 May 2011 (UTC)

Take a look at the complex analysis section of the ramification article. Then take a look at the statement section of the article on the Riemann–Hurwitz formula. Notice that you have been asked to consider the map ƒ(z) = z² which has a ramification of order two, and the Riemann sphere whose Euler characteristic is also two. Finally, the automorphism section of the Möbius transformation article tells us that the automorphisms of the Riemann sphere are the Möbius transformations. — Fly by Night (talk) 01:50, 14 May 2011 (UTC)

So I see that we can deduce from the formula that my f ramifies at exactly 2 points with multiplicity 2 in each case, right? So are we saying you can map these via T to any other 2 points on the Riemann sphere: do we want these to be 0 and infinity? Even if I have understood that far, I'm not quite following where you go from there, sorry.

I did have 1 further query while I'm waiting, if anyone can help me with it: I am trying to work out, with the Riemann surface R associated with complete analytic function $f(z)=(z^{2}-1)^{1/2}+(z^{2}-4)^{1/2}$ on $U=\mathbb {C} -\{\pm 1,\,\pm 2\}$ and regular covering map $\pi :R\to U$, what subgroup of the full symmetric group of $\pi ^{-1}(P)$ is obtained from all closed curves starting and ending at P (since these curves 'lift' to curves between preimages of P under the covering map, each gives a permutation of the preimages of the point P, via the starting/end point of the lifted curve). However, I'm having trouble figuring out how we can actually find out what permutations are possible via these curves: there are 4 preimages to every point under this map, right? (2 from the squaring map and two from the fact that the square root is a multi-valued function) So where do I go from here? I would really be very grateful for your help or advice on both of these problems :) Totenines99 (talk) 14:24, 14 May 2011 (UTC)

May 14

Statistics text

Hello. I'm looking for a good, rigourous, calculus-based introductory statistics text. It should start from the very basics (i.e., assuming you don't even know what a mean is [though I do], not basic as in starting from field theory because that is too basic :), kind of an equivalent to Spivak's calculus text. Does anyone have any recommendations? Thanks. 72.128.95.0 (talk) 15:37, 14 May 2011 (UTC)

I don't really know a lot of statistics textbooks, but you can try All of statistics. It starts at the beginning, but it's very condensed, it tries to cover a lot of technical ground without too much discussion. -- Meni Rosenfeld (talk) 08:28, 15 May 2011 (UTC)

Simple formula tom figure out kilobytes per second to number of hours?

Can anyone give me a simple formula to figure out how long it will take to download a file given a constant number of kilobytes per second and knowing the total size of the file in gigabytes? It would be easier for me to see the calculation I think with a real example so say I am downloading at a constant rate of 92 kilobytes per second and the file I am downloading is 13.4 gigabytes. I know I have to do something like multiplying the number of kbs by 60 to get to minutes and then 60 to get to hours and then dividing somehow into the number of gbs expressed in kbs but I get lost in the details. Thanks.--108.54.17.250 (talk) 15:12, 14 May 2011 (UTC)

You divide the file size by the download rate to get the number of seconds. Divide by 60 to get minutes, and by 60 again to get hours. In your example, you have 13.4 gigabytes = 13400000 kilobytes divided by 92 kilobytes/second to get 145652 seconds. Divide by 60 seconds/minute to get 2427 minutes. Divide by 60 minutes per hour for 40 hours. Detailed numbers are slightly different if you use base-2 gigabytes, instead of base 10, and if you don't just drop fractions. --Stephan Schulz (talk) 16:30, 14 May 2011 (UTC)

Great. Thank you. So its convert file size in gb → kb/kbs/60/60.--108.54.17.250 (talk) 16:42, 14 May 2011 (UTC)

To put it as simply as possible, divide the file size (in gigabytes) by the download rate (in kilobytes per second), and then multiply the result by 278 -- this will give you the time in hours. (Reason: 1 GB/hr = 278 kB/sec)Looie496 (talk) 17:00, 14 May 2011 (UTC)

Be careful mind, some transfer rates are given in kilobits per second (kbit/s, kb/s, or kbps) and there are 8 kilobits to the kilobyte. Grandiose (me, talk, contribs) 17:04, 14 May 2011 (UTC)

To further complicate things, often people write "gigabyte" when they really mean gibibyte. Also (though this may be irrelevant for the OP), sometimes the electrical bitrate is specified, and with 8b/10b encoding one data byte is 10 electrical bits. -- Meni Rosenfeld (talk) 08:21, 15 May 2011 (UTC)

Note that if you actually attempt to download 13.4 GB, your ISP is likely to stop you or slow the transfer rate down to a crawl. And, even if they don't, the download is likely to be interrupted anyway, so you need a way to restart an interrupted download. StuRat (talk) 04:17, 16 May 2011 (UTC)

Google: [1]. Sławomir Biały (talk) 12:09, 16 May 2011 (UTC)

May 15

Ellipse

The equation $ax^{2}+bxy+cy^{2}=1$ describes an ellipse, but it is not a standard ellipse because the ellipse's axes are not necessarily parallel to the x and y axes, i.e. it has been rotated. How do you read the angle of rotation from the equation? Widener (talk) 03:13, 15 May 2011 (UTC)

If the major axis forms an angle of $\theta$ with the x-axis, then θ minimizes the value of $ax^{2}+bxy+cy^{2}$ with the substitution $(x,y)=(\cos \theta ,\sin \theta )$. Substituting and differentiating gives $(c-a)\sin(2\theta )+b\cos(2\theta )=0$ which means $\theta ={\tfrac {1}{2}}\tan ^{-1}\left({\frac {b}{a-c}}\right)$. This gives the result up to a multiple of $\pi /2$. -- Meni Rosenfeld (talk) 08:17, 15 May 2011 (UTC)

Did this reply help you? -- Meni Rosenfeld (talk) 15:56, 16 May 2011 (UTC)

Multiplication of Cardinals and Order Preservation.

See Multiplication#Properties. If a, b, and c are cardinal numbers, does the following still hold?

" Multiplication by a positive number preserves order: if a > 0, then if b > c then ab > ac. Multiplication by a negative number reverses order: if a < 0 and b > c then ab < ac."
Thanks in advance. voidnature 08:24, 15 May 2011 (UTC)

[ec]Are you referring to cardinal numbers? I don't know of a way to multiply a cardinal number with a negative number. For multiplication by a cardinal number a, this will hold if either $a<b$ or b is finite. -- Meni Rosenfeld (talk) 08:34, 15 May 2011 (UTC)

Yes, I am referring to cardinal numbers. My question is actually concentrated on this bit :"if a > 0, then if b > c then ab > ac". Thankyou. voidnature 08:36, 15 May 2011 (UTC)

Ok, so you need either $a<b$ or b finite. Otherwise, a counterexample is $a=\aleph _{0},b=\aleph _{0},c=1$. However, it will always be true that $ab\geq ac$. I think the axiom of choice might be needed for some of these results. -- Meni Rosenfeld (talk) 08:49, 15 May 2011 (UTC)

Oops, sorry, c has to be zero. So I don't need to worry about $a=\aleph _{0},b=\aleph _{0}$. So my question should be If a and b are cardinal numbers and c is 0, does "if a > 0, then if b > c then ab > ac" hold? Thankyou. voidnature 08:58, 15 May 2011 (UTC)

Every cardinal multiplied by 0 is 0, so you're basically asking, "if a>0 and b>0 are cardinal numbers, is ab>0?" The answer is yes, because the cartesian product of two nonempty sets is nonempty. -- Meni Rosenfeld (talk) 09:05, 15 May 2011 (UTC)

"the cartesian product of two nonempty sets is nonempty": can you give a proof please? voidnature 09:09, 15 May 2011 (UTC)

$a\in A,\ b\in B\Rightarrow (a,b)\in A\times B$. -- Meni Rosenfeld (talk) 10:17, 15 May 2011 (UTC)

Discriminants in number fields and rings of integers

Hello everyone. I've been asked to 'describe' the ring of integers ${\mathcal {O}}_{K}$ for $K=\mathbb {Q} [X]/(X^{3}+2x+1)$. I know the discriminant of this polynomial is -59, I know that it is irreducible, and I also know that if M is a sub-$\mathbb {Z}$-module of ${\mathcal {O}}_{K}$ of index r and M is closed under multiplication then disc(M)=$r^{2}$disc( ${\mathcal {O}}_{K}$). However, perhaps I'm getting confused with my concepts and definitions here: AFAIK the discriminant of K is given by the determinant of the matrix whose elements are the inner products of a $\mathbb {Z}$-basis for K: but I don't really understand then what the discriminant of ${\mathcal {O}}_{K}$ is going to be, or how we relate the two (or indeed how we can 'describe' ${\mathcal {O}}_{K}$. I have a feeling understanding is on the tip of my mental tongue, but I haven't quite grasped it yet, so if anyone could help that would be great. I suspect that ${\mathcal {O}}_{K}=\mathbb {Q} [X]/(X^{3}+2x+1)$, but I'm not sure how to prove it rigorously if I am correct. Thanks! Mathmos6 (talk) 13:56, 15 May 2011 (UTC)

Why is S5 a modal companion of CPC?

Why is S5 a modal companion of CPC? It seems like this should imply that S5 implies the translation of excluded middle, which seems to be $\Box p\lor \Box \lnot p$, which seems to say there are no contingent propositions - but surely S5 allows for contingent propositions? 88.104.173.35 (talk) 19:27, 15 May 2011 (UTC)

Plane partitioning algorithm

Resolved

Oh, this is on the tip of my tongue: I hate when that happens. Begins with "L", I think... I'm trying to remember the name of an algorithm which takes an array of points on a plane and partitions the plane such that each point is surrounded by a polygon - I think the margins of which fall equidistantly with another point (or is it some other definition of "influence"?). The resulting diagram looks like a honeycomb made by tipsy bees. What is that algorithm? (it's not a BSP or its ilk)-- Finlay McWalter ☻ Talk 22:22, 15 May 2011 (UTC)

Voronoi diagram perhaps?--RDBury (talk) 23:39, 15 May 2011 (UTC)

Yes, that's it (and no L in sight)! Thanks. -- Finlay McWalter ☻ Talk 23:45, 15 May 2011 (UTC)

“L, I KNOW it begins with L!” – b_jonas 18:46, 16 May 2011 (UTC)

May 16

Black Scholes Transformation

This is a basic calculus question. I'm reading this book and on page 102 there is the Black Scholes equation

${\frac {\partial V}{\partial t}}+{\frac {\sigma ^{2}(t)}{2}}S^{2}{\frac {\partial ^{2}V}{\partial S^{2}}}+r(t)S{\frac {\partial V}{\partial S}}-r(t)V=0$

and the following substitutions are made

${\bar {S}}=Se^{\alpha (t)}$

${\bar {V}}=Ve^{\beta (t)}$

${\bar {t}}=\gamma (t)$

to turn the original equation into the following:

${\frac {d\gamma }{dt}}{\frac {\partial {\bar {V}}}{\partial {\bar {t}}}}+{\frac {\sigma ^{2}(t)}{2}}{\bar {S}}^{2}{\frac {\partial ^{2}{\bar {V}}}{\partial {\bar {S}}^{2}}}+(r(t)+{\frac {d\alpha }{dt}}){\bar {S}}{\frac {\partial {\bar {V}}}{\partial {\bar {S}}}}-(r(t)+{\frac {d\beta }{dt}}){\bar {V}}=0$

What's going on here exactly? I can't put my finger on where the terms in the transformations are coming from, I know it must be some sort of application of the chain rule but I don't see what exactly. —Preceding unsigned comment added by 130.102.158.15 (talk) 04:30, 16 May 2011 (UTC)

The formula you've listed is the partial differential equation version of the Black-Scholes formula. I believe the substitutions establish the boundary conditions for the solution. You can find more about this on page 440, here: http://faculty.atu.edu/mfinan/actuarieshall/DFEM.pdf. —Preceding unsigned comment added by 12.186.80.1 (talk) 20:16, 16 May 2011 (UTC)

Your best off working backwards. Go through the second equation doing all the differentiation and you should see that you get back to the first equation. (Assuming it's correct, I haven't actually checked it.) --Tango (talk) 20:20, 16 May 2011 (UTC)

Area enclosed by ellipse equation

How do you find the area enclosed by the ellipse $ax^{2}+bxy+cy^{2}=1$ assuming the coefficients are chosen such that the equation yields an ellipse (rather than a hyperbola). Widener (talk) 06:40, 16 May 2011 (UTC)

Per ellipse, the area is ${\frac {2\pi }{\sqrt {4ac-b^{2}}}}$. Dragons flight (talk) 06:49, 16 May 2011 (UTC)

Fancy that! Is there a derivation or proof? Widener (talk) 06:59, 16 May 2011 (UTC)

The proof is about two lines if you use the fact that the discriminant is an invariant on binary quadratic forms. I don't think they cover that much in undergraduate curricula nowadays though.--RDBury (talk) 12:02, 16 May 2011 (UTC)

Generating sequences based on probabilities

I want to create a set of fixed-length sequences based on an a priori set of probabilities describing the distribution of symbols in the resulting set of sequences. The case where the probability of each position is independent is simple enough (simply pick each symbol randomly according to probability), but I'm at a bit of a loss as how to approach the problem if the input probabilities also specify the joint probability of multiple positions.

Perhaps a toy example will make things clearer. Take a three position binary sequence A,B,C. The input to the problem is probabilities for a symbol at each position, e.g p(A=1) = 0.6; p(B=1) = 0.5; p(C=1) = 0.55. Given those probabilities, I want to create a set of output sequences that, in the limit, would satisfy those probabilities. While simple enough for independent positions, I'm also interested in cases where joint probabilities are also specified, e.g. p(A=1,B=1) = 0.3; p(B=1,C=0) = 0.2; p(A=1,C=1) = 0.25. I'm not sure how to generate the sequence when there's not just a single probability to satisfy per position, but a web of interlocking probabilities. - As I said, that's just a toy example for explanatory purposes. The cases that I'm looking into are more complicated, with potentially dozens of positions and dozens of symbols at each position, so enumerative approaches aren't going to work. The joint probabilities would be limited to pairs of positions, though. (But approaches that are extensible to triples or quartets of positions would be all the better.) Any suggestions or pointers? Thanks. -- 140.142.20.229 (talk) 17:32, 16 May 2011 (UTC)

This is not solvable on the basis of the information provided. Without some extra information such as independence or second-order-independence, the joint probabilities do not determine the global probabilities, and you need to know the global probabilities in order to generate exemplars. (Bayesian techniques sometimes make use of joint probabilities of this sort, but they are not guaranteed to give the correct answer.) Looie496 (talk) 17:41, 16 May 2011 (UTC)

I'm not familiar with the concept of "second-order-independence", so am I right in assuming that it's the three event version of two-event independence (e.g. p(X,Y) = p(X)p(Y))? If so, yes, I should have stated that that can be assumed. Basically, the given probabilities are the only constraints on the system. Having the other degrees of freedom being as unbiased as possible is preferred, although if biasing them slightly is a way to make the problem more tractable, I'm open to it. As I mentioned, the problem is somewhat trivial if you can assume (pairwise) independence, but one of my issues is that I'm not sure how the three-plus event version of independence would behave (where there's nothing special about the probability distribution of triples of events that isn't captured by the probabilities of the individual events and pairs of events; like with pairwise p(X,Y) = p(X)p(Y) independence there's nothing about the probability of the pair of events that isn't captured by the probabilities of the single events), or even if it would simplify the problem. -- 140.142.20.229 (talk) 20:40, 16 May 2011 (UTC)

I would do this by first having a validity check - if any position has more than one symbol, the sequence is not valid. Then, calculate each probability. Say you set A=1/B=1 in the first probability and then you set B=0/C=1 in the following probability. This is not a valid sequence because B cannot be 1 and 0 at the same time. Quit and try again. Set that in a loop to try it over and over and over until a valid sequence appears. I just used this tactic because I lost my key for a piece of software. I knew the range and probabilities of most of the elements of the key, so I wrote a program to randomly generate keys until one of them passed the software's key check. In your cause, the validity check would be the same as the key check I used. -- kainaw™ 17:59, 16 May 2011 (UTC)

If I'm understanding you correctly, you're suggesting to select A,B, and C based on their individual probabilities, and then go through the list of pair probabilities, and then do random number draws and checks for each one? For example, We randomly pick ABC to be 110. We then look at the AB pair, draw a random number, say 0.25, find it passes the p(A=1,B=1) = 0.3 check, and move on to the BC pair. We pull another random number, say 0.65, and find it fails the p(B=1,C=0) = 0.2 check. We then throw out the selection, and regenerate an ABC sequence from scratch. - My concern with that is with a large number of pair probabilities, the procedure would be highly inefficient as the repeated tests mean most generated sequences would randomly fail at least one of the pair probability tests. -- 140.142.20.229 (talk) 20:51, 16 May 2011 (UTC)

Normal subgroups

I'm trying to study for an exam, and this is one of the review questions listed on the textbook author's website:

Q: If N is a normal subgroup and |aN| = n, then a^n = e. 
A: false
Remark: a^n belongs to N.

I can't see for the life of me why a^n should belong to N. Isn't |aN|=n just |N|, regardless of what a is, and regardless of whether N is normal? By substitution, that would seem to imply that a^(|N|) belongs to N, for any element a and for any subgroup N, which can't possibly be right... 71.176.168.114 (talk) 19:35, 16 May 2011 (UTC)

|aN| doesn't necessarily equal |N|. Consider N=Z_2 (ie. integers mod 2, so it has order 2) and a=2. aN is then the trivial group, so has order 1. --Tango (talk) 20:27, 16 May 2011 (UTC)

OK, you're right, but I still don't see the leap to "a^n belongs to N." Can you explain that or give me a hint? 71.176.168.114 (talk) 20:32, 16 May 2011 (UTC)

I think that |aN| = n is supposed to mean that the order of the element aN in the quotient group G/N is n. Matthew Auger (talk) 21:09, 16 May 2011 (UTC)

Thank you 71.176.168.114 (talk) 21:15, 16 May 2011 (UTC)

Is there a word for a (position, orientation) pair?

It is something I use so commonly in geometry I'm amazed that after Googling I have not found a good word for it. Together the two describe 6 degrees of freedom of an object in relation to a defined axis system, typically

X, Y, Z, yaw, pitch and roll

There are many different ways of representing both the position and orientation parts. Any suggestions, no matter how informal, are welcome as long as it makes intuitive sense - I'm trying to choose a good type name in a program I'm writing.

196.215.115.184 (talk) 20:21, 16 May 2011 (UTC)Eon

Congruence, isometry, isometric map, movement? – b_jonas 20:29, 16 May 2011 (UTC)

They are examples of generalized coordinates. I don't know a more specific term. --Tango (talk) 20:32, 16 May 2011 (UTC)

Thanks, I think configuration is the best general word I could find so far after following your links. Actually, I thought posientation is a cool word to describe that. It turns out I'm not the first person on the internet to have thought of that! 196.215.115.184 (talk) 20:59, 16 May 2011 (UTC)Eon

What about pose? It's a term that comes up a lot in engineering when speaking of such matters.--Leon (talk) 21:59, 16 May 2011 (UTC)