Tesseract

Tesseract Hypercube (8-cell)
Type	Regular polychoron
Cells	8 (4.4.4)
Faces	24 {4}
Edges	32
Vertices	16
Vertex configuration	4 (4.4.4) (tetrahedron)
Schläfli symbol	{4,3,3}
Symmetry group	group [3,3,4]
Dual	16-cell
Properties	convex

Vertex figure: tetrahedron

In geometry, the tesseract is the 4-dimensional analog of the cube. That is, the tesseract is to the cube as the cube is to the square. More formally, the tesseract can be described as a regular convex 4-polytope with eight cubical cells. The word tesseract is believed to have been coined by Charles Howard Hinton.

Generalizations of the cube to dimensions greater than three are called hypercubes or measure polytopes. This article focuses on the 4D hypercube, the tesseract.

Geometry

The standard tesseract in Euclidean 4-space is given as the convex hull of the points (±1, ±1, ±1, ±1). That is, it consists of the points:

$\{(x_{1},x_{2},x_{3},x_{4})\in \mathbb {R} ^{4}\,:\,-1\leq x_{i}\leq 1\}.$

A tesseract is bounded by eight hyperplanes (x_i = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.

Since each vertex of a tesseract is adjacent to four edges, the vertex figure of the tesseract is a regular tetrahedron. Thus the tesseract is given Schläfli symbol {4,3,3}. The dual polytope of the tesseract is called the hexadecachoron, or 16-cell, with Schläfli symbol {3,3,4}.

Projections to 2 dimensions

This structure is not easily imagined but it is possible to project tesseracts into three- or two-dimensional spaces. Furthermore, projections on the 2D-plane become more instructive by rearranging the positions of the projected vertices. In this fashion, one can obtain pictures that no longer reflect the spatial relationships within the tesseract, but which illustrate the connection structure of the vertices. The following examples are provided:

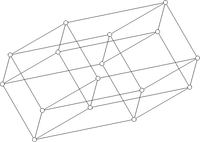
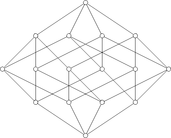
The first illustration shows how a tesseract is in principle obtained by combining two cubes. The scheme is similar to the construction of a cube from two squares: juxtapose two copies of the lower dimensional cube and connect the corresponding vertices. The second picture accounts for the fact that each edge of a tesseract is of the same length. This picture also enables the human brain to find a multitude of cubes that are nicely interconnected. The third diagram finally orders the vertices of the tesseract with respect to the distance along the edges, with respect to the bottom point. This view is of interest when using tesseracts as the basis for a network topology to link multiple processors in parallel computing: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.

The connection pattern of the tesseract's vertices is the same as that of a 4×4 square array drawn on a torus; each cell (representing a vertex of the tesseract) is adjacent to exactly four other cells. See geometry of the 4x4 square. Tesseracts are also bipartite graphs, just as a path, rectangle, cube and tree are.

Projections to 3 dimensions

The cell-first parallel projection of the tesseract into 3-dimensional space has a cubical envelope. The nearest and farthest cells are projected onto the cube, and the remaining 6 cells are projected onto the 6 square faces of the cube.

The face-first parallel projection of the tesseract into 3-dimensional space has a cuboidal envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the 4 remaining cells project to the side faces.

The edge-first parallel projection of the tesseract into 3-dimensional space has an envelope in the shape of a hexagonal prism. The 8 cells project onto volumes in the shape of parallelogrammic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto 6 parallelograms in a hexagonal envelope under vertex-first projection.

The vertex-first parallel projection of the tesseract into 3-dimensional space has a rhombic dodecahedral envelope. There are exactly two ways of decomposing a rhombic dodecahedron into 4 congruent parallelepipeds, giving a total of 8 possible parallelopipeds. The images of the tesseract's cells under this projection are precisely these 8 parallelopipeds. This projection is also the one with maximal volume.

In a sense, in a 4-dimensional world with "wind", the net of a tessaract would be extremely unstable and would be knocked over, "flattening" the "cubeface" that the net falls onto. This is similar to how a 2-dimensional net of a cube would be unstable with wind, falling over on one of its two sides.

Tesseracts in art and literature

A net of a tesseract.

Robert A. Heinlein mentioned hypercubes in at least three of his science fiction stories. In “—And He Built a Crooked House—” (1940), he described a house built as a net (i.e., an unfolding of the cells into three-dimensional space) of a tesseract. It collapsed, becoming a real 4-dimensional tesseract. Stephen Baxter's short story collection 'Vacuum Diagrams' includes a similar structure, in which the internal layout of rooms in a house is deeply confusing to the characters exploring it.

Heinlein's 1963 novel Glory Road included the foldbox, a hyperdimensional packing case that was bigger inside than outside. 1963 also saw the debut of long-running BBC television serial Doctor Who, in which the main character pilots a time machine called a TARDIS, which is built with technology that makes it "dimensionally transcendental", that is, bigger inside than out. Although Glory Road would have been available to the creators of Doctor Who when they were developing the show it is quite possible that they arrived at the idea independently.

A hypercube is also used as the main deus ex machina of Robert J. Sawyer's book Factoring Humanity (ISBN 0765309033), even appearing on its North American cover.

The tesseract is mentioned in the children's fantasy novel A Wrinkle In Time, by Madeleine L'Engle, as a way of introducing the concept of higher dimensions, but the treatment is extremely vague. In that book she uses the tesseract as a portal, a doorway which you can pass through and emerge far away from the starting point, as if the two distant points were brought together at one intersection (at the tesseract doorway) by the folding of space-time, enabling near-instantaneous transportation.

In Alex Garland's 1998 novel "The Tesseract", the author uses the term to mean the three-dimensional net of the four-dimensional hypercube rather than the hypercube itself. It is a metaphor for the characters' inability to understand the causes behind the events which shape their lives: they can only visualize the superficial world they inhabit.

In the novel Mythago Wood (and its sequels) by Robert Holdstock there is a landscape within the wood that is far larger on the inside than the outside. It distorts time and features its own distinct time zones. People and creatures are formed by some force in the wood interacting with the human subconscious mind and tapping into buried memories of ancient myths and events. From these the wood generates creatures and places within its own vast space.

The movie Cube 2: Hypercube focuses on eight strangers trapped inside a "hypercube", or a net of connected hypercubes.

Hypercubes and all kinds of multi-dimensional space and structures star prominently in many books by Rudy Rucker.

The DC Comics crossover DC One Million showed a future Earth in which cities occupied extradimensional areas called tesseracts, leaving the planet's surface unspoiled. Similar technology was used for Superman's current Fortress of Solitude, and was used as storage space in the headquarters of the original incarnation (pre-Zero Hour) of the Legion of Super-Heroes.

The television series Andromeda makes use of tesseract generators as a plot device. These are primarily intended to manipulate space (also referred to as phase shifting) but often cause problems with time as well.

Another TV series, Strange Days at Blake Holsey High (also known as Black Hole High), features an episode (The Tesseract) where Lucas gets trapped in a tesseract. Lucas calls someone he thinks will help (Corrine), but she gets sucked into the tesseract. Eventually, the school folds up in time as well as space. With the help of a "disappeared" teacher, Lucas unfolds the tesseract. The episode gave a good description of a tesseract (see [1]).

In the Infocom text adventure, Spellbreaker, the climax of the story features a tesseract constructed by various featureless white cubes, each of which has magical property corresponding to the base elements of the universe.

In Finnegans Wake by James Joyce, the main protagonist HCE transforms into a tesseract ("Wherefore let it hardly by any being thinking be said either or thought that the prisoner of that sacred edifice, were he an Ivor the Boneless or an Olaf the Hide, was at his best a onestone parable, a rude breathing on the void of to be, a venter hearing his own bauchspeech in backwords, or, more strictly, but tristurned initials, the cluekey to a worldroom beyond the roomwhorld, for scarce one, or pathetically few of his dode canal sammenliverscared seriously or for long to doubt with Kurt Iuld van Dijke (the gravitational pull perceived by certain fixed residents and the capture of uncertain comets chancedrifting through our system suggesting an authenticitatem of his aliquitudinis) the canonicity of his existence as a tesseract. Be still, O quick! Speak him dumb! Hush ye fronds of Ulma!").

The painting "Crucifixion (Corpus Hypercubus)", by Salvador Dalí, 1954, depicts the crucified Jesus upon the net of a hypercube. It is featured at the Metropolitan Museum of Art. See [2]

The Nextwave comic book by Marvel Comics features a vehicle called the Shockwave Rider that contains 5 tesseract zones inside of it.

Hypercubes in Computer Science

In computer science, the term hypercube refers to a specific type of parallel computer, whose processors, or processing elements (PEs), are interconnected in the same way as the vertices of a hypercube.

Thus, an n-dimensional hypercube computer has 2ⁿ PEs, each directly connected to n other PEs.

Examples include the nCUBE machines used to win the first Gordon Bell Prize, the Caltech Cosmic Cube and the Connection Machine, the latter using the hypercube topology to connect groups of processors.

See also

• 3-sphere
• cross-polytope
• simplex
• polychoron
• list of regular polytopes
• fourth dimension
• Runcinated tesseract

External links

• HyperSolids is an open source program for the Apple Macintosh (Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
• an illustration (requires Java)
• Hypercube 98 A Windows program that displays animated hypercubes, by Rudy Rucker
• Flash Demonstration and Interactive Hypercube (requires Flash)
• ken perlin's home page A way to visualize hypercubes, by Ken Perlin
• Magic Cube 4D - Tesseract version of Rubik's Cube
• [3] - Java applet version of tesseract Rubik's Cube
• Two equators - HTML pages showing a tesseract and pentatope rotating on two mutually perpendicular axes
• Cut The Knot!: The Tesseract: An interactive column using Java applets at cut-the-knot
• http://www.dogfeathers.com/java/hyprcube.html Animated Hypercube
• Geometry of the 4×4 square points out vertex-adjacency properties.
• Polytope Viewer - Java applet for projecting and manipulating hypercubes and other polytopes
• Greg Egan's page