Truncated order-6 square tiling: Difference between revisions

Content deleted Content added

Inline

Revision as of 04:40, 30 October 2014

Truncated order-6 square tiling
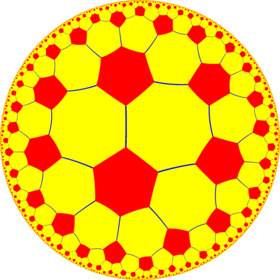Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	8.8.6
Schläfli symbol	t{4,6}
Wythoff symbol	2 6 \| 4
Coxeter diagram
Symmetry group	[6,4], (642) [(3,3,4)], (334)
Dual	Order-4 hexakis hexagonal tiling
Properties	Vertex-transitive

In geometry, the truncated order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{4,6}.

Uniform colorings

The half symmetry [1⁺,6,4] = [(4,4,3)] can be shown with alternating two colors of octagons.	The dual tiling represents the fundamental domains of the *443 orbifold, shown in two different centers here.

Symmetry

The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and cyan, and mirrors exist on the boundaries between colors. The symmetry can be doubled as 642 symmetry by adding a mirror bisecting the fundamental domain.

A larger subgroup is constructed [(4,4,3^*)], index 6, as (3*22) with gyration points removed, becomes (*222222).

Small index subgroup symmetries of [(4,4,3)] (*443)
Subgroup index	1	2		6
Diagram
Coxeter (orbifold)	[(4,4,3)] (*443)	[(4,1⁺,4,3)] (*3232)	[(4,4,3⁺)] (3*22)	[(4,4,3)] (222222)
Rotation subgroups
Subgroup index	2	4		12
Diagram
Coxeter (orbifold)	[(4,4,3)]⁺ (443)	[(4,1⁺,4,3⁺)] (3232)		[(4,1⁺,4,3*)] (222222)

Related polyhedra and tiling

From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular order-4 hexagonal tiling.

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.

Uniform tetrahexagonal tilings v t e
*Symmetry: [6,4], (642)** (with [6,6] (662), [(4,3,3)] (443) , [∞,3,∞] (3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (3232) index 4 subsymmetry)
= = =	=	= = =	=	= = =	=

{6,4}	t{6,4}	r{6,4}	t{4,6}	{4,6}	rr{6,4}	tr{6,4}
Uniform duals


V6⁴	V4.12.12	V(4.6)²	V6.8.8	V4⁶	V4.4.4.6	V4.8.12
Alternations
[1⁺,6,4] (*443)	[6⁺,4] (6*2)	[6,1⁺,4] (*3222)	[6,4⁺] (4*3)	[6,4,1⁺] (*662)	[(6,4,2⁺)] (2*32)	[6,4]⁺ (642)
=	=	=	=	=	=

h{6,4}	s{6,4}	hr{6,4}	s{4,6}	h{4,6}	hrr{6,4}	sr{6,4}

It can also be generated from the (4 4 3) hyperbolic tilings:

Uniform (4,4,3) tilings v t e
Symmetry: [(4,4,3)] (*443)							[(4,4,3)]⁺ (443)	[(4,4,3⁺)] (3*22)	[(4,1⁺,4,3)] (*3232)



h{6,4} t₀(4,4,3)	h₂{6,4} t_0,1(4,4,3)	{4,6}¹/₂ t₁(4,4,3)	h₂{6,4} t_1,2(4,4,3)	h{6,4} t₂(4,4,3)	r{6,4}¹/₂ t_0,2(4,4,3)	t{4,6}¹/₂ t_0,1,2(4,4,3)	s{4,6}¹/₂ s(4,4,3)	hr{4,6}¹/₂ hr(4,3,4)	h{4,6}¹/₂ h(4,3,4)	q{4,6} h₁(4,3,4)
Uniform duals

V(3.4)⁴	V3.8.4.8	V(4.4)³	V3.8.4.8	V(3.4)⁴	V4.6.4.6	V6.8.8	V3.3.3.4.3.4	V(4.4.3)²	V6⁶	V4.3.4.6.6

*n42 symmetry mutation of truncated tilings: n.8.8 v t e
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracompact
Symmetry *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Truncated figures
Config.	2.8.8	3.8.8	4.8.8	5.8.8	6.8.8	7.8.8	8.8.8	∞.8.8
n-kis figures
Config.	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

References

John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
"Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links

@@ Line 12: / Line 12: @@
 == Symmetry ==
-The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The symmetry can be doubled as [[642 symmetry]] by adding a mirror bisecting the fundamental domain.
+The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and cyan, and mirrors exist on the boundaries between colors. The symmetry can be doubled as [[642 symmetry]] by adding a mirror bisecting the fundamental domain.
 A larger subgroup is constructed [(4,4,3<sup>*</sup>)], index 6, as (3*22) with gyration points removed, becomes (*222222).
@@ Line 22: / Line 22: @@
 !1
 !colspan=2|2
+!6
 |- align=center
 !Diagram
@@ Line 27: / Line 28: @@
 |[[File:443_symmetry_0a0.png|120px]]
 |[[File:443_symmetry_a0a.png|120px]]
+|[[File:443_symmetry_z0z.png|120px]]
 |-
 ![[Coxeter notation|Coxeter]]<BR>([[Orbifold notation|orbifold]])
@@ Line 33: / Line 34: @@
 ![(4,1<sup>+</sup>,4,3)]<BR>{{CDD|labelh|node|split1-44|branch_c2}}<BR>([[3232 symmetry|*3232]])
 ![(4,4,3<sup>+</sup>)]<BR>{{CDD|node_c1|split1-44|branch_h2h2}}<BR>(3*22)
+![(4,4,3*)]<BR>{{CDD|node_c1|split1-44|2}}<BR>(*222222)
 |-
-!colspan=4|Rotation subgroups
+!colspan=5|Rotation subgroups
 |- align=center
 !Subgroup index
 !2
 !colspan=2|4
+!12
 |- align=center
 !Diagram
 |[[File:443_symmetry_aaa.png|120px]]
 |colspan=2|[[File:443_symmetry_abc.png|120px]]
+|[[File:443_symmetry_zaz.png|120px]]
 |-
 !Coxeter<BR>(orbifold)
 ![(4,4,3)]<sup>+</sup><BR>{{CDD|node_h2|split1-44|branch_h2h2}}<BR>(443)
 !colspan=2|[(4,1<sup>+</sup>,4,3<sup>+</sup>)]<BR>{{CDD|labelh|node|split1-44|branch_h2h2}}<BR>(3232)
+![(4,1<sup>+</sup>,4,3*)]<BR>{{CDD|labelh|node|split1-44|}}<BR>(222222)
 |}