Homes's law: Difference between revisions
| Line 1: | Line 1: | ||
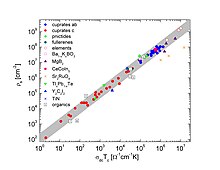
[[File:Universal scaling line.JPG|thumbnail|A log-log plot of the superfluid density versus the product of the |
[[File:Universal scaling line.JPG|thumbnail|A log-log plot of the superfluid density versus the product of the |
||
dc conductivity and the critical temperature for: cuprates (''a-b'' plane and ''c'' axis), pnictides, |
dc conductivity and the critical temperature for: cuprates (''a-b'' plane and ''c'' axis), pnictides, |
||
elements, TiN, Ba<sub> |
elements, TiN, Ba<sub>1−x</sub>K<sub>x</sub>BiO<sub>3</sub>, MgB<sub>2</sub>, organic SC, fullerenes, |
||
heavy fermion CeCoIn<sub>5</sub>, negative-U induced SC Tl<sub>x</sub>Pb<sub> |
heavy fermion CeCoIn<sub>5</sub>, negative-U induced SC Tl<sub>x</sub>Pb<sub>1−x</sub>Te and |
||
Y<sub>2</sub>C<sub>2</sub>I<sub>2</sub>. The grey stripe corresponds to ρ<sub>s0</sub> = |
Y<sub>2</sub>C<sub>2</sub>I<sub>2</sub>. The grey stripe corresponds to ρ<sub>s0</sub> = |
||
(110 ± 60) σ<sub>dc</sub> T<sub>c</sub> (the units are the same as those in the original |
(110 ± 60) σ<sub>dc</sub> T<sub>c</sub> (the units are the same as those in the original |
||
Revision as of 16:54, 5 March 2017
In superconductivity, Homes's law is an empirical relation that states that a superconductor's
critical temperature (Tc) is proportional to the strength of the superconducting state for temperatures well below Tc close to zero temperature (also referred to as the fully formed superfluid density, ) multiplied by the electrical resistivity measured just above the critical temperature. In cuprate high-temperature superconductors the relation follows the form
,
or alternatively
.
Many novel superconductors are anisotropic, so the resistivity and the superfluid density are tensor quantities; the superscript denotes the crystallographic direction along which these quantities are measured. Note that this expression assumes that the conductivity and temperature have both been recast in units of cm−1 (or s−1), and that the superfluid density has units of cm−2 (or s−2); the constant is dimensionless. The expected form for a BCS dirty-limit superconductor has slightly larger numerical constant of ~8.1.
The law is named for physicist Christopher Homes and was first presented in the July 29, 2004 edition of Nature,[1] and was the subject of a News and Views article by Jan Zaanen in the same issue[2] in which he speculated that the high transition temperatures observed in the cuprate superconductors are because the metallic states in these materials are as viscous as permitted by the laws of quantum physics. A more detailed version of this scaling relation subsequently appeared in Physical Review B in 2005,[3] in which it was argued that any material that falls on the scaling line is likely in the dirty limit (superconducting coherence length ξ0 is much greater than the normal-state mean-free path l, ξ0≫ l); however, a paper by Vladimir Kogan in Physical Review B in 2013 has shown that the scaling relation is valid even when ξ0~ l,[4] suggesting that only materials in the clean limit (ξ0≪ l) will fall off of this scaling line.
Francis Pratt and Stephen Blundell have argued that Homes's law is violated in the organic superconductors. This work was first presented in Physical Review Letters in March 2005.[5] On the other hand, it has been recently demonstrated by Sasa Dordevic and coworkers that if the dc conductivity and the superfluid density are measured on the same sample at the same time using either infrared or microwave impedance spectroscopy, then the organic superconductors do indeed fall on the universal scaling line, along with a number of other exotic superconductors. This work was published in Scientific Reports in 2013.[6]
References
- ^ C. C. Homes; et al. (2004). "A universal scaling relation in high-temperature superconductors". Nature (London). 430 (6999): 539–541. arXiv:cond-mat/0404216. Bibcode:2004Natur.430..539H. doi:10.1038/nature02673.
- ^ Zaanen, Jan (2004). "Superconductivity: Why the temperature is high". Nature (London). 430 (6999): 512–513. Bibcode:2004Natur.430..512Z. doi:10.1038/430512a.
- ^ C. C. Homes; S. V. Dordevic; T. Valla; M. Strongin (2005). "Scaling of the superfluid density in high-temperature superconductors". Phys. Rev. B. 72: 134517. arXiv:cond-mat/0410719. Bibcode:2005PhRvB..72m4517H. doi:10.1103/PhysRevB.72.134517.
- ^ V. G. Kogan (2013). "Homes scaling and BCS". Phys. Rev. B. 87: 220507(R). arXiv:1305.3487. Bibcode:2013PhRvB..87v0507K. doi:10.1103/PhysRevB.87.220507.
- ^ F. L. Pratt; S. J. BLundell (2005). "Universal Scaling Relations in Molecular Superconductors". Phys. Rev. Lett. 94: 097006. arXiv:cond-mat/0411754. Bibcode:2005PhRvL..94i7006P. doi:10.1103/PhysRevLett.94.097006.
- ^ S. V. Dordevic; D. N. Basov; C. C. Homes (2012). "Do organic and other exotic superconductors fail universal scaling relations?". Sci. Rep. 3: 1713. arXiv:1305.0019. Bibcode:2013NatSR...3E1713D. doi:10.1038/srep01713.





