CPCTC: Difference between revisions
No edit summary |
m Reverted edits by 2602:306:80C3:EA30:0:0:0:42 (talk): Editing tests (HG) (3.1.22) |
||
| Line 1: | Line 1: | ||
[[Image:Congruent triangles.png|right|Two congruent triangles]] |
[[Image:Congruent triangles.png|right|Two congruent triangles]] |
||
In [[geometry]], '''"Corresponding parts of congruent triangles are congruent"''' ('''CPCTC''') is a succinct statement of a theorem regarding [[congruence (geometry)|congruent]] [[trigonometry]], defined as triangles either of which is an [[isometry]] of the other.<ref>{{cite web|url=http://www.cliffsnotes.com/math/geometry/triangles/congruent-triangles|title=Congruent Triangles|publisher=Cliff's Notes|accessdate=2014-02-04}}</ref> |
In [[geometry]], '''"Corresponding parts of congruent triangles are congruent"''' ('''CPCTC''') is a succinct statement of a theorem regarding [[congruence (geometry)|congruent]] [[trigonometry]], defined as triangles either of which is an [[isometry]] of the other.<ref>{{cite web|url=http://www.cliffsnotes.com/math/geometry/triangles/congruent-triangles|title=Congruent Triangles|publisher=Cliff's Notes|accessdate=2014-02-04}}</ref> CPC4C states that if two or more triangles are congruent, then all of their corresponding angles and sides are congruent as well. CPCTC is useful in proving various theorems about triangles and other polygons.<ref>{{cite web|url=http://www.mathwarehouse.com/geometry/congruent_triangles/congruent-parts-CPCTC.php|title=CPCTC means 'Corresponding parts of congruent triangles are congruent' and...|publisher=Mathware House|accessdate=2014-02-04}}</ref> |
||
If triangles ABC and DEF are congruent, denoted as |
If triangles ABC and DEF are congruent, denoted as |
||
| Line 28: | Line 28: | ||
{{elementary-geometry- |
{{elementary-geometry-stub}} |
||
Revision as of 03:05, 5 September 2017
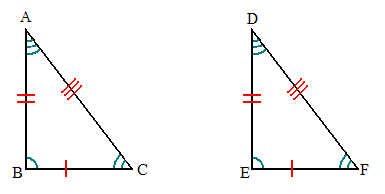
In geometry, "Corresponding parts of congruent triangles are congruent" (CPCTC) is a succinct statement of a theorem regarding congruent trigonometry, defined as triangles either of which is an isometry of the other.[1] CPC4C states that if two or more triangles are congruent, then all of their corresponding angles and sides are congruent as well. CPCTC is useful in proving various theorems about triangles and other polygons.[2]
If triangles ABC and DEF are congruent, denoted as
with corresponding pairs of angles at vertices A, D; B, E; and C, F, and with corresponding pairs of sides AB, DE; BC, EF; and CA, FD, then the following statements are true:
A related theorem is CPCFC, in which "triangles" is replaced with "figures" so that the theorem applies to any pair of polygons or polyhedrons that are congruent.
References
- ^ "Congruent Triangles". Cliff's Notes. Retrieved 2014-02-04.
- ^ "CPCTC means 'Corresponding parts of congruent triangles are congruent' and..." Mathware House. Retrieved 2014-02-04.
corresponding parts of congruent triangles are congruent
External links







