Pappus graph: Difference between revisions
fix deadlink |
book thickness and queue number |
||
| Line 13: | Line 13: | ||
| chromatic_index = 3 |
| chromatic_index = 3 |
||
| properties = [[Bipartite graph|Bipartite]]<br>[[Symmetric graph|Symmetric]]<br>[[Distance-transitive graph|Distance-transitive]]<br>[[Distance-regular graph|Distance-regular]]<br>[[Cubic graph|Cubic]]<br>[[Hamiltonian graph|Hamiltonian]] |
| properties = [[Bipartite graph|Bipartite]]<br>[[Symmetric graph|Symmetric]]<br>[[Distance-transitive graph|Distance-transitive]]<br>[[Distance-regular graph|Distance-regular]]<br>[[Cubic graph|Cubic]]<br>[[Hamiltonian graph|Hamiltonian]] |
||
|book thickness=3|queue number=2}} |
|||
}} |
|||
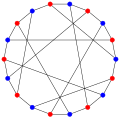
In the [[mathematics|mathematical]] field of [[graph theory]], the '''Pappus graph''' is a [[Bipartite graph|bipartite]] 3-[[regular graph|regular]] [[undirected graph]] with 18 vertices and 27 edges, formed as the [[Levi graph]] of the [[Pappus configuration]].<ref>{{MathWorld|urlname=PappusGraph|title=Pappus Graph}}</ref> It is named after [[Pappus of Alexandria]], an ancient [[Greek mathematics|Greek mathematician]] who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the [[cubic graph|cubic]] [[distance-regular graph]]s are known; the Pappus graph is one of the 13 such graphs.<ref>Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989.</ref> |
In the [[mathematics|mathematical]] field of [[graph theory]], the '''Pappus graph''' is a [[Bipartite graph|bipartite]] 3-[[regular graph|regular]] [[undirected graph]] with 18 vertices and 27 edges, formed as the [[Levi graph]] of the [[Pappus configuration]].<ref>{{MathWorld|urlname=PappusGraph|title=Pappus Graph}}</ref> It is named after [[Pappus of Alexandria]], an ancient [[Greek mathematics|Greek mathematician]] who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the [[cubic graph|cubic]] [[distance-regular graph]]s are known; the Pappus graph is one of the 13 such graphs.<ref>Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989.</ref> |
||
The Pappus graph has [[Crossing number (graph theory)|rectilinear crossing number]] 5, and is the smallest cubic graph with that crossing number {{OEIS|id=A110507}}. It has [[Girth (graph theory)|girth]] 6, diameter 4, radius 4, [[chromatic number]] 2, [[chromatic index]] 3 and is both 3-[[k-vertex-connected graph|vertex-connected]] and 3-[[k-edge-connected graph|edge-connected]]. |
The Pappus graph has [[Crossing number (graph theory)|rectilinear crossing number]] 5, and is the smallest cubic graph with that crossing number {{OEIS|id=A110507}}. It has [[Girth (graph theory)|girth]] 6, diameter 4, radius 4, [[chromatic number]] 2, [[chromatic index]] 3 and is both 3-[[k-vertex-connected graph|vertex-connected]] and 3-[[k-edge-connected graph|edge-connected]]. It has [[book thickness]] 3 and [[queue number]] 2.<ref>Jessica Wolz, ''Engineering Linear Layouts with SAT.'' Master Thesis, University of Tübingen, 2018</ref> |
||
The Pappus graph has a [[chromatic polynomial]] equal to: <math>(x-1)x(x^{16}-26x^{15}+325x^{14}-2600x^{13}+14950x^{12}-65762x^{11}+</math><math>229852x^{10}-653966x^9+1537363x^8-3008720x^7+4904386x^6-</math><math>6609926x^5+7238770x^4-6236975x^3+3989074x^2-1690406x+356509)</math>. |
The Pappus graph has a [[chromatic polynomial]] equal to: <math>(x-1)x(x^{16}-26x^{15}+325x^{14}-2600x^{13}+14950x^{12}-65762x^{11}+</math><math>229852x^{10}-653966x^9+1537363x^8-3008720x^7+4904386x^6-</math><math>6609926x^5+7238770x^4-6236975x^3+3989074x^2-1690406x+356509)</math>. |
||
Revision as of 13:22, 17 April 2018
| Pappus graph | |
|---|---|
 The Pappus graph. | |
| Named after | Pappus of Alexandria |
| Vertices | 18 |
| Edges | 27 |
| Radius | 4 |
| Diameter | 4 |
| Girth | 6 |
| Automorphisms | 216 |
| Chromatic number | 2 |
| Chromatic index | 3 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Bipartite Symmetric Distance-transitive Distance-regular Cubic Hamiltonian |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Pappus graph is a bipartite 3-regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration.[1] It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic distance-regular graphs are known; the Pappus graph is one of the 13 such graphs.[2]
The Pappus graph has rectilinear crossing number 5, and is the smallest cubic graph with that crossing number (sequence A110507 in the OEIS). It has girth 6, diameter 4, radius 4, chromatic number 2, chromatic index 3 and is both 3-vertex-connected and 3-edge-connected. It has book thickness 3 and queue number 2.[3]
The Pappus graph has a chromatic polynomial equal to: .
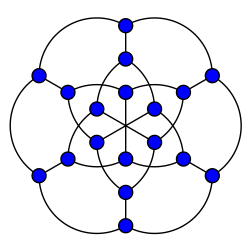
The name "Pappus graph" has also been used to refer to a related nine-vertex graph,[4] with a vertex for each point of the Pappus configuration and an edge for every pair of points on the same line; this nine-vertex graph is 6-regular, is the complement graph of the union of three disjoint triangle graphs, and is the complete tripartite graph K3,3,3. The first Pappus graph can be embedded in the torus to form a self-Petrie dual regular map with nine hexagonal faces; the second, to form a regular map with 18 triangular faces. The two regular toroidal maps are dual to each other.
Algebraic properties
The automorphism group of the Pappus graph is a group of order 216. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Pappus graph is a symmetric graph. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Pappus graph, referenced as F018A, is the only cubic symmetric graph on 18 vertices.[5][6]
The characteristic polynomial of the Pappus graph is . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
Gallery
-
Pappus graph coloured to highlight various cycles.
-
The chromatic index of the Pappus graph is 3.
-
The chromatic number of the Pappus graph is 2.
-
The Pappus graph embedded in the torus, as a regular map with nine hexagonal faces.
References
- ^ Weisstein, Eric W. "Pappus Graph". MathWorld.
- ^ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989.
- ^ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- ^ Kagno, I. N. (1947), "Desargues' and Pappus' graphs and their groups", American Journal of Mathematics, 69 (4), The Johns Hopkins University Press: 859–863, doi:10.2307/2371806, JSTOR 2371806
- ^ Royle, G. "Cubic Symmetric Graphs (The Foster Census)."
- ^ Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002.