Nerve complex

Constructing the nerve of an open good cover containing 3 sets in the plane.

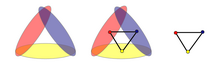
In topology, the nerve of an open covering is a construction of an abstract simplicial complex from an open covering of a topological space X that captures many of the interesting topological properties in an algorithmic or combinatorial way. It was introduced by Pavel Alexandrov and now has many variants and generalisations, among them the Čech nerve of a cover, which in turn is generalised by hypercoverings.

Alexandrov's definition

Let X be a topological space. Let $I$ be an index set. Let $C$ be a family indexed by $I$ of open subsets of X: $C=\lbrace U_{i}:i\in I\rbrace$. The nerve of $C$ is a set of finite subsets of the index-set $I$. It contains all finite subsets $J\subseteq I$ such that the intersection of the U_i whose subindices are in J is non-empty:

N(C)  := ${\bigg \{}J\subseteq I:~~~~\bigcap _{j\in J}U_{j}\neq \varnothing {\bigg \}}$

N(C) may contain singletons (elements i in $I$ such that U_i is non-empty), pairs (pairs of elements of i,j in $I$ such that U_i intersects U_j), triplets, and so on. If J belongs to N(C), then any of its subsets is also in N(C). Therefore N(C) is an abstract simplicial complex and it is often called the nerve complex of C.

Examples

1. Let X be the circle S¹ and C = {U₁, U₂}, where U₁ is an arc covering the upper half of S¹ and U₂ is an arc covering its lower half, with some overlap at both sides (they must overlap at both sides in order to cover all of S¹). Then N(C) = { {1}, {2}, {1,2} }, which is an abstract 1-simplex.

2. Let X be the circle S¹ and C = {U₁, U₂, U₃}, where each U_i is an arc covering one third of S¹, with some overlap with the adjacent U_i. Then N(C) = { {1}, {2}, {3}, {1,2}, {2,3}, {3,1} }. Note that {1,2,3} is not in N(C) since the common intersection of all three sets is empty.

The Nerve Lemma

If C is a general open cover, the complex N(C) need not reflect the topology of X accurately. For example, we can cover any n-sphere with two contractible sets U₁ and U₂ that have a non-empty intersection, as in example 1 above. In this case, N(C) is an abstract 1-simplex.

The nerve lemma states that, if C is a good cover (i.e., an open cover in which any finite intersection of sets is contractible: for each finite $J\subset I$ the set $\bigcap _{i\in J}U_{i}$ is contractible), then the nerve N(C) is homotopy-equivalent to $\bigcup _{i\in I}U_{i}$. For instance, a circle covered by three open arcs, intersecting in pairs in one arc as in example 2 above, is modelled by a homeomorphic complex, the geometrical realization of N(C).

The Čech nerve

Given an open cover $C=\{U_{i}:i\in I\}$ of a topological space $X$, or more generally a cover in a site, we can regard the pairwise fibre products $U_{ij}=U_{i}\times _{X}U_{j}$, which in the case of a topological space is precisely the intersection $U_{i}\cap U_{j}$. The collection of all such intersections can be referred to as $C\times _{X}C$ and the triple intersections as $C\times _{X}C\times _{X}C$.

By considering the natural maps $U_{ij}\to U_{i}$ and $U_{i}\to U_{ii}$, we can construct a simplicial object $S(C)_{\bullet }$ defined by $S(C)_{n}=C\times _{X}\cdots \times _{X}C$, n-fold fibre product. This is the Čech nerve, and by taking connected components we get a simplicial set, which we can realise topologically: $|S(\pi _{0}(C))|$.

The nerve theorem

If the covering and the space are sufficiently nice, for instance if $X$ is compact and all intersections of sets in the cover are contractible or empty, then the space $|S(\pi _{0}(C))|$ is weakly equivalent to $X$. This is known as the nerve theorem.

See also

• Hypercovering