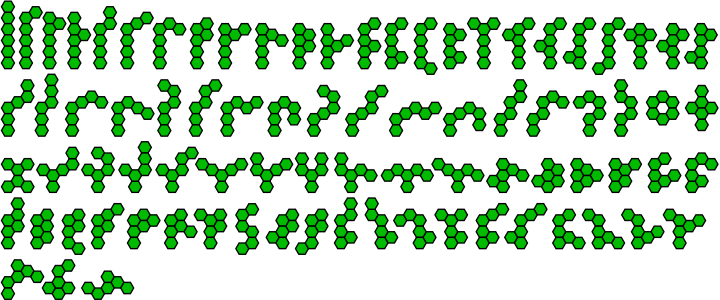Polyhex (mathematics): Difference between revisions
| Line 34: | Line 34: | ||
Of the polyhexes shown in the table, 2 have 6-fold rotation and reflection symmetry (thus also 3-fold and 2-fold symmetry), the monohex and the hexahex with a hole, 3 others have 3-fold rotation (the compact trihex, the pinwheel tetrahex and the hexahex looking like an equilateral triangle) and 3-fold reflection symmetry, 9 others have 2-fold rotation and reflection, 8 have just two fold rotation, 16 just have 2-fold reflection and the other 78 (most of the tetrahexes, pentahexes or hexahexes) are asymmetrical. The tilings of most of the reflection-symmetrical polyhexes are also invariant under glide reflections of the same order by the length of the polyhex. No polyhex has an order of symmetry greater than six for reflection, rotation or glide. |
Of the polyhexes shown in the table, 2 have 6-fold rotation and reflection symmetry (thus also 3-fold and 2-fold symmetry), the monohex and the hexahex with a hole, 3 others have 3-fold rotation (the compact trihex, the pinwheel tetrahex and the hexahex looking like an equilateral triangle) and 3-fold reflection symmetry, 9 others have 2-fold rotation and reflection, 8 have just two fold rotation, 16 just have 2-fold reflection and the other 78 (most of the tetrahexes, pentahexes or hexahexes) are asymmetrical. The tilings of most of the reflection-symmetrical polyhexes are also invariant under glide reflections of the same order by the length of the polyhex. No polyhex has an order of symmetry greater than six for reflection, rotation or glide. |
||
{| cellspacing=32 |
|||
== Monohex== |
|||
| ⚫ | |||
|- |
|||
There is one monohex: |
|||
|The Dihex: ||[[Image:Dicomb.svg|The Dihex]] |
|||
| ⚫ | |||
|- |
|||
==Dihex== |
|||
| ⚫ | |||
There is one dihex: |
|||
|- |
|||
:[[Image:Dicomb.svg|The Dihex]] |
|||
==Trihexes== |
|||
|- |
|||
There are 3 trihexes: |
|||
| ⚫ | |||
| ⚫ | |||
|- |
|||
==Tetrahexes== |
|||
| ⚫ | |||
There are 7 tetrahexes: |
|||
|} |
|||
:[[Image:Tetracomb.svg|The 7 Tetrahexes]] |
|||
==Pentahexes== |
|||
There are 22 pentahexes: |
|||
| ⚫ | |||
==Hexahexes== |
|||
There are 82 hexahexes: |
|||
| ⚫ | |||
==See also== |
==See also== |
||
Revision as of 21:07, 28 December 2020
In recreational mathematics, a polyhex is a polyform with a regular hexagon (or 'hex' for short) as the base form.
As with polyominoes, polyhexes may be enumerated as free polyhexes (where rotations and reflections count as the same shape), fixed polyhexes (where different orientations count as distinct) and one-sided polyhexes (where mirror images count as distinct but rotations count as identical). They may also be distinguished according to whether they may contain holes. The number of free n-hexes for n = 1, 2, 3, … is 1, 1, 3, 7, 22, 82, 333, 1448, … (sequence A000228 in the OEIS); the number of free polyhexes with holes is given by OEIS: A038144; the number of free polyhexes without holes is given by OEIS: A018190; the number of fixed polyhexes is given by OEIS: A001207; the number of one-sided polyhexes is given by OEIS: A006535.[1][2]
| n | Free | Free with holes | Free without holes | One-sided | Fixed |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 1 | 3 |
| 3 | 3 | 0 | 3 | 3 | 11 |
| 4 | 7 | 0 | 7 | 10 | 44 |
| 5 | 22 | 0 | 22 | 33 | 186 |
| 6 | 82 | 1 | 81 | 147 | 814 |
| 7 | 333 | 2 | 331 | 620 | 3652 |
| 8 | 1448 | 13 | 1435 | 2821 | 16689 |
| 9 | 6572 | 67 | 6505 | 12942 | 77359 |
| 10 | 30490 | 404 | 30086 | 60639 | 362671 |
Tessellation properties
All of the polyhexes with fewer than five hexagons can form at least one regular plane tiling. In addition, the plane tilings of the dihex and straight polyhexes are invariant under 180 degrees rotation or reflection parallel or perpendicular to the long axis of the dihex (order 2 rotational and order 4 reflection symmetry), and the hexagon tiling and some other polyhexes (like the hexahex with one hole, below) are invariant under 60, 120 or 180 degree rotation (order 6 rotational and reflection symmetry).
In addition, the hexagon is a hexiamond, so all polyhexes are also distinct polyiamonds. Also, as an equilateral triangle is a hexagon and three smaller equilateral triangles it is possible to superimpose a large polyiamond on any polyhex, giving two polyiamonds corresponding to each polyhex. This is used as the basis of an infinite division of a hexagon into smaller and smaller hexagons (an irrep-tiling) or into hexagons and triangles.
Of the polyhexes shown in the table, 2 have 6-fold rotation and reflection symmetry (thus also 3-fold and 2-fold symmetry), the monohex and the hexahex with a hole, 3 others have 3-fold rotation (the compact trihex, the pinwheel tetrahex and the hexahex looking like an equilateral triangle) and 3-fold reflection symmetry, 9 others have 2-fold rotation and reflection, 8 have just two fold rotation, 16 just have 2-fold reflection and the other 78 (most of the tetrahexes, pentahexes or hexahexes) are asymmetrical. The tilings of most of the reflection-symmetrical polyhexes are also invariant under glide reflections of the same order by the length of the polyhex. No polyhex has an order of symmetry greater than six for reflection, rotation or glide.
Monohex
There is one monohex:
Dihex
There is one dihex:
Trihexes
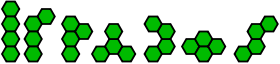
There are 3 trihexes:
Tetrahexes
There are 7 tetrahexes:
Pentahexes
There are 22 pentahexes:
Hexahexes
There are 82 hexahexes:
See also
- Tessellation
- Percolation theory
- Polyiamond – tilings with equilateral triangles
- Polyomino – tilings with squares
- Polycyclic aromatic hydrocarbon – hydrocarbons whose structure is based on polyhexes
- Rep-tile – tilings of shapes that are made of smaller copies of themselves
References
- ^ Wolfram Mathworld: Polyhex
- ^ Glenn C. Rhoads, Planar tilings by polyominoes, polyhexes, and polyiamonds, Journal of Computational and Applied Mathematics 174 (2005), No. 2, pp 329–353