Unit cell: Difference between revisions

Content deleted Content added

Inline

Revision as of 02:26, 23 July 2021

In geometry, biology, mineralogy, and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice.^[1]

The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell. The unit cell is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations.

There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is the smallest possible unit cell. In some cases, the full symmetry of a crystal structure is not obvious from the primitive cell, in which cases a conventional cell may be used. A conventional cell (which may or may not be primitive) is a unit cell with the full symmetry of the lattice and may include more than one lattice point. The conventional unit cells are parallelotope in n dimensions.

Primitive cell

A primitive cell is a unit cell that contains only one and exactly one lattice point. For unit cells generally, lattice points that are shared by $n$ cells are counted as ⁠1/ $n$ ⁠ of the lattice points contained in each of those cells; so for example a primitive unit cell in three dimensions which has lattice points only at its eight vertices is considered to contain ⁠1/8⁠ of each of them.^[2] An alternative conceptualization is to consistently pick only one of the $n$ lattice points to belong to the given unit cell (so the other $1-n$ lattice points belong to adjacent unit cells).

The primitive translation vectors $a \to 1$ , $a \to 2$ , $a \to 3$ span a lattice cell of smallest volume for a particular three-dimensional lattice, and are used to define a crystal translation vector

{\vec {T}}=u_{1}{\vec {a}}_{1}+u_{2}{\vec {a}}_{2}+u_{3}{\vec {a}}_{3},

where $u 1$ , $u 2$ , $u 3$ are integers, translation by which leaves the lattice invariant.^{[note 1]} That is, for a point in the lattice $r$ , the arrangement of points appears the same from $r' = r + T \to$ as from $r$ .^[3]

Since the primitive cell is defined by the primitive axes (vectors) $a \to 1$ , $a \to 2$ , $a \to 3$ , the volume $V p$ of the primitive cell is given by the parallelepiped from the above axes as

V_{\mathrm {p} }=\left|{\vec {a}}_{1}\cdot ({\vec {a}}_{2}\times {\vec {a}}_{3})\right|.

Wigner–Seitz cell

In addition to the parallelepiped primitive cells, for every Bravais lattice there is another kind of primitive cell called the Wigner–Seitz cell. In the Wigner–Seitz cell, the lattice point is at the center of the cell, and for most Bravais lattices, the shape is not a parallelogram or parallelepiped. This is a type of Voronoi cell. The Wigner–Seitz cell of the reciprocal lattice in momentum space is called the Brillouin zone.

Conventional cell

For each particular lattice, a conventional cell has been chosen on a case-by-case basis by crystallographers based on convenience of calculation.^[4] These conventional cells may have additional lattice points located in the middle of the faces or body of the unit cell. The number of lattice points, as well as the volume, of the conventional cell is an integer multiple (typically 1, 2, 3, or 4) of that of the primitive cell.^[5]

Two dimensions

For any 2-dimensional lattice, the unit cells are parallelograms, which in special cases may have orthogonal angles, or equal lengths, or both. Some of the five two-dimensional Bravais lattices are represented using conventional primitive cells, as shown below.

Conventional primitive cell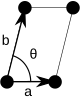
Shape name	Parallelogram	Rectangle	Square
Bravais lattice	Primitive Oblique	Primitive Rectangular	Primitive Square

The centered rectangular lattice also has a primitive cell in the shape of a rhombus, but in order to allow easy discrimination on the basis of symmetry, it is represented by a conventional cell which contains two lattice points.

Primitive cell
Shape name	Rhombus
Conventional cell
Bravais lattice	Centered Rectangular

Three dimensions

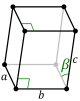
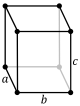
For any 3-dimensional lattice, the conventional unit cells are parallelepipeds, which in special cases may have orthogonal angles, or equal lengths, or both. Some of the fourteen three-dimensional Bravais lattices are represented using conventional primitive cells, as shown below.

Conventional primitive cell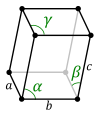
Shape name	Parallelepiped	Oblique rectangular prism	Rectangular cuboid	Square cuboid	Trigonal trapezohedron	Cube
Bravais lattice	Primitive Triclinic	Primitive Monoclinic	Primitive Orthorhombic	Primitive Tetragonal	Primitive Rhombohedral	Primitive Cubic

The other Bravais lattices also have primitive cells in the shape of a parallelepiped, but in order to allow easy discrimination on the basis of symmetry, they are represented by conventional cells which contain more than one lattice point.

Primitive cell
Shape name	Oblique rhombic prism	Right rhombic prism
Conventional cell
Bravais lattice	Base-centered Monoclinic	Base-centered Orthorhombic

Notes

^ In $n$ dimensions the crystal translation vector would be
${\vec {T}}=\sum _{i=1}^{n}u_{i}{\vec {a}}_{i},\quad {\mbox{where }}u_{i}\in \mathbb {Z} \quad \forall i.$
That is, for a point in the lattice $r$ , the arrangement of points appears the same from $r' = r + T \to$ as from $r$ .

References

^ Ashcroft, Neil W. (1976). "Chapter 4". Solid State Physics. W. B. Saunders Company. p. 72. ISBN 0-03-083993-9.
^ "DoITPoMS – TLP Library Crystallography – Unit Cell". Online Materials Science Learning Resources: DoITPoMS. University of Cambridge. Retrieved 21 February 2015.
^ Kittel, Charles. Introduction to Solid State Physics (8 ed.). Wiley. p. 4. ISBN 978-0-471-41526-8.
^ Aroyo, M. I., ed. (2016-12-31). "International Tables for Crystallography". International Tables for Crystallography. Chester, England: International Union of Crystallography. p. 25. doi:10.1107/97809553602060000114. ISBN 978-0-470-97423-0.
^ Ashcroft, Neil W. (1976). Solid State Physics. W. B. Saunders Company. p. 73. ISBN 0-03-083993-9.

[first-3] In $n$ dimensions the crystal translation vector would be
${\vec {T}}=\sum _{i=1}^{n}u_{i}{\vec {a}}_{i},\quad {\mbox{where }}u_{i}\in \mathbb {Z} \quad \forall i.$
That is, for a point in the lattice $r$ , the arrangement of points appears the same from $r' = r + T \to$ as from $r$ .

[1] Ashcroft, Neil W. (1976). "Chapter 4". Solid State Physics. W. B. Saunders Company. p. 72. ISBN 0-03-083993-9.

[doitpoms-2] "DoITPoMS – TLP Library Crystallography – Unit Cell". Online Materials Science Learning Resources: DoITPoMS. University of Cambridge. Retrieved 21 February 2015.

[4] Kittel, Charles. Introduction to Solid State Physics (8 ed.). Wiley. p. 4. ISBN 978-0-471-41526-8.

[5] Aroyo, M. I., ed. (2016-12-31). "International Tables for Crystallography". International Tables for Crystallography. Chester, England: International Union of Crystallography. p. 25. doi:10.1107/97809553602060000114. ISBN 978-0-470-97423-0.

[6] Ashcroft, Neil W. (1976). Solid State Physics. W. B. Saunders Company. p. 73. ISBN 0-03-083993-9.

[1]

[2]

[note 1]

[3]

[4]

[5]

@@ Line 7: / Line 7: @@
 The concept is used particularly in describing [[crystal structure]] in two and three dimensions, though it makes sense in all dimensions.  A lattice can be characterized by the geometry of its unit cell. The unit cell is a section of the tiling (a [[parallelogram]] or [[parallelepiped]]) that generates the whole tiling using only translations.
-There are two special cases of the unit cell: the '''primitive cell''' and the '''conventional cell'''. The primitive cell is a unit cell corresponding to a single [[lattice point]], it is the smallest possible unit cell. In some cases, the full symmetry of a crystal structure is not obvious from the primitive cell, in which cases a conventional cell may be used. A conventional cell (which may or may not be primitive) is the smallest unit cell with the full symmetry of the lattice and may include more than one lattice point. The conventional unit cells are [[Parallelepiped#Parallelotope|parallelotope]] in n dimensions.
+There are two special cases of the unit cell: the '''primitive cell''' and the '''conventional cell'''. The primitive cell is a unit cell corresponding to a single [[lattice point]], it is the smallest possible unit cell. In some cases, the full symmetry of a crystal structure is not obvious from the primitive cell, in which cases a conventional cell may be used. A conventional cell (which may or may not be primitive) is a unit cell with the full symmetry of the lattice and may include more than one lattice point. The conventional unit cells are [[Parallelepiped#Parallelotope|parallelotope]] in n dimensions.
 ==Primitive cell==
@@ Line 72: / Line 72: @@
 ==Three dimensions==
 [[File:Parallelepiped 2013-11-29.svg|thumb|A [[parallelepiped]] is a general primitive cell for 3-dimensional space.]]
-For any 3-dimensional lattice, the unit cells are [[parallelepiped]]s, which in special cases may have orthogonal angles, or equal lengths, or both. Some of the fourteen three-dimensional [[Bravais lattice]]s are represented using conventional primitive cells, as shown below.
+For any 3-dimensional lattice, the conventional unit cells are [[parallelepiped]]s, which in special cases may have orthogonal angles, or equal lengths, or both. Some of the fourteen three-dimensional [[Bravais lattice]]s are represented using conventional primitive cells, as shown below.
 {| class=wikitable