Jump to content

Zero to the power of zero: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
→Polynomials and power series: Postpone the less elementary stuff about ring-valued coefficients to the end of the sentence. Disambiguate "identity element". No need to define the term "evaluation homomorphism". Postpone use of R[x] until it is stated that it is a ring, to shorten the exposition. Remove reference to Cauchy product since no one actually refers to polynomial multiplication as this.
→Polynomials and power series: It is less confusing to use r instead of a, since the coefficients are called a_i. Remove the technicality "(unique)" which is anyway clear from the definite article.
Line 12: Line 12:


==Polynomials and power series==
==Polynomials and power series==
Likewise, when working with [[polynomial]]s, it is convenient to define {{math|0<sup>0</sup>}} as having the value {{math|1}}. A (real) polynomial is an expression of the form {{math|''a''<sub>0</sub>''x''<sup>0</sup> + ⋅⋅⋅ + ''a''<sub>''n''</sub>''x''<sup>''n''</sup>}}, where {{math|''x''}} is an indeterminate, and the coefficients {{math|''a''<sub>''n''</sub>}} are real numbers. Polynomials are added termwise, and multiplied by applying the [[distributive law]] and the usual rules for exponents. With these algebraic rules for manipulation, polynomials form a [[polynomial ring|ring]] {{math|'''R'''[''x'']}}. The polynomial {{math|''x''<sup>0</sup>}} is the [[multiplicative identity]] of the polynomial ring, meaning that it is the (unique) element such that {{math|''x''<sup>0</sup>}} times any polynomial {{math|''p''(''x'')}} is just {{math|''p''(''x'')}}.<ref name="Bourbaki_1970_1" /> Polynomials can be evaluated by specializing {{math|''x''}} to a real number. More precisely, for any given real number {{math|''a''}}, there is a unique unital [[algebra homomorphism|{{math|'''R'''}}-algebra homomorphism]] {{math|ev<sub>''a''</sub> : '''R'''[''x''] → '''R'''}} such that {{math|1=ev<sub>''a''</sub>(''x'') = ''a''}}. Because {{math|ev<sub>''a''</sub>}} is unital, {{math|1=ev<sub>''a''</sub>(''x''<sup>0</sup>) = 1}}. That is, {{math|1=''a''<sup>0</sup> = 1}} for each real number {{math|''a''}}, including 0. The same argument applies with {{math|'''R'''}} replaced by any [[ring_(mathematics)|ring]].<ref name="Bourbaki_1970_2" />
Likewise, when working with [[polynomial]]s, it is convenient to define {{math|0<sup>0</sup>}} as having the value {{math|1}}. A (real) polynomial is an expression of the form {{math|''a''<sub>0</sub>''x''<sup>0</sup> + ⋅⋅⋅ + ''a''<sub>''n''</sub>''x''<sup>''n''</sup>}}, where {{math|''x''}} is an indeterminate, and the coefficients {{math|''a''<sub>''n''</sub>}} are real numbers. Polynomials are added termwise, and multiplied by applying the [[distributive law]] and the usual rules for exponents. With these algebraic rules for manipulation, polynomials form a [[polynomial ring|ring]] {{math|'''R'''[''x'']}}. The polynomial {{math|''x''<sup>0</sup>}} is the [[multiplicative identity]] of the polynomial ring, meaning that it is the element such that {{math|''x''<sup>0</sup>}} times any polynomial {{math|''p''(''x'')}} is just {{math|''p''(''x'')}}.<ref name="Bourbaki_1970_1" /> Polynomials can be evaluated by specializing {{math|''x''}} to a real number. More precisely, for any given real number {{math|''r''}}, there is a unique unital [[algebra homomorphism|{{math|'''R'''}}-algebra homomorphism]] {{math|ev<sub>''r''</sub> : '''R'''[''x''] → '''R'''}} such that {{math|1=ev<sub>''r''</sub>(''x'') = ''r''}}. Because {{math|ev<sub>''r''</sub>}} is unital, {{math|1=ev<sub>''r''</sub>(''x''<sup>0</sup>) = 1}}. That is, {{math|1=''r''<sup>0</sup> = 1}} for each real number {{math|''r''}}, including 0. The same argument applies with {{math|'''R'''}} replaced by any [[ring_(mathematics)|ring]].<ref name="Bourbaki_1970_2" />


Defining {{math|1=0<sup>0</sup> = 1}} is necessary for many polynomial identities. For example, the [[binomial theorem]] {{math|1=(1 + ''x'')<sup>''n''</sup> = ∑{{su|b=''k''=0|p=''n''|lh=1em}} {{big|(}}{{su|p=''n''|b=''k''}}{{big|)}} ''x''<sup>''k''</sup>}} is not valid for {{math|1=''x'' = 0}} unless {{math|1=0<sup>0</sup> = 1}}.<ref name="T4n3B" />
Defining {{math|1=0<sup>0</sup> = 1}} is necessary for many polynomial identities. For example, the [[binomial theorem]] {{math|1=(1 + ''x'')<sup>''n''</sup> = ∑{{su|b=''k''=0|p=''n''|lh=1em}} {{big|(}}{{su|p=''n''|b=''k''}}{{big|)}} ''x''<sup>''k''</sup>}} is not valid for {{math|1=''x'' = 0}} unless {{math|1=0<sup>0</sup> = 1}}.<ref name="T4n3B" />

Revision as of 05:08, 10 August 2021

Zero to the power of zero, denoted by 00, is a mathematical expression with no agreed-upon value. The most common possibilities are 1 or leaving the expression undefined, with justifications existing for each, depending on context. In algebra and combinatorics, the generally agreed upon value is 00 = 1, whereas in mathematical analysis, the expression is sometimes left undefined. Computer programming languages and software also have differing ways of handling this expression.

Discrete exponents

Many widely used formulas involving natural-number exponents require 00 to be defined as 1. For example, the following three interpretations of b0 make just as much sense for b = 0 as they do for positive integers b:

All three of these specialize to give 00 = 1.

Polynomials and power series

Likewise, when working with polynomials, it is convenient to define 00 as having the value 1. A (real) polynomial is an expression of the form a0x0 + ⋅⋅⋅ + anxn, where x is an indeterminate, and the coefficients an are real numbers. Polynomials are added termwise, and multiplied by applying the distributive law and the usual rules for exponents. With these algebraic rules for manipulation, polynomials form a ring R[x]. The polynomial x0 is the multiplicative identity of the polynomial ring, meaning that it is the element such that x0 times any polynomial p(x) is just p(x).[2] Polynomials can be evaluated by specializing x to a real number. More precisely, for any given real number r, there is a unique unital R-algebra homomorphism evr : R[x] → R such that evr(x) = r. Because evr is unital, evr(x0) = 1. That is, r0 = 1 for each real number r, including 0. The same argument applies with R replaced by any ring.[3]

Defining 00 = 1 is necessary for many polynomial identities. For example, the binomial theorem (1 + x)n = ∑n
k=0 (n
k) xk is not valid for x = 0 unless 00 = 1.[4]

Similarly, rings of power series require x0 to be defined as 1 for all specializations of x. For example, identities like ⁠1/1−x⁠ = ∑∞
n=0 xn and ex = ∑∞
n=0 ⁠xn/n!⁠ hold for x = 0 only if 00 = 1.[5]

In calculus, the power rule ⁠d/dx⁠xn = nxn−1 is valid for n = 1 at x = 0 only if 00 = 1.

Continuous exponents

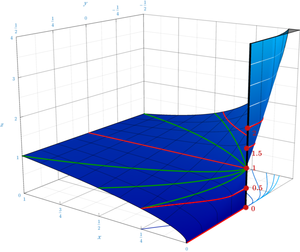
Plot of z = xy. The red curves (with z constant) yield different limits as (x, y) approaches (0, 0). The green curves (of finite constant slope, y = ax) all yield a limit of 1.

Limits involving algebraic operations can often be evaluated by replacing subexpressions by their limits; if the resulting expression does not determine the original limit, the expression is known as an indeterminate form.[6] The expression 00 is an indeterminate form: Given real-valued functions f(t) and g(t) approaching 0 (as t approaches a real number or ±∞) with f(t) > 0, the limit of f(t)g(t) can be any non-negative real number or +∞, or it can diverge, depending on f and g. For example, each limit below involves a function f(t)g(t) with f(t), g(t) → 0 as t → 0+ (a one-sided limit), but their values are different:

Thus, the two-variable function xy, though continuous on the set {(x, y) : x > 0}, cannot be extended to a continuous function on {(x, y) : x > 0} ∪ {(0, 0)}, no matter how one chooses to define 00.[7]

On the other hand, if f and g are both analytic functions on an open neighborhood of a number c, then f(t)g(t) → 1 as t approaches c from any side on which f is positive.[8]

Complex exponents

In the complex domain, the function zw may be defined for nonzero z by choosing a branch of log z and defining zw as ew log z. This does not define 0w since there is no branch of log z defined at z = 0, let alone in a neighborhood of 0.[9][10][11]

History

As a value

In 1752, Euler in Introductio in analysin infinitorum wrote that a0 = 1[12] and explicitly mentioned that 00 = 1.[13] An annotation attributed[14] to Mascheroni in a 1787 edition of Euler's book Institutiones calculi differentialis[15] offered the "justification" as well as another more involved justification. In the 1830s, Libri[16][14] published several further arguments attempting to justify the claim 00 = 1, though these were far from convincing, even by standards of rigor at the time.[17]

As a limiting form

Euler, when setting 00 = 1, mentioned that consequently the values of the function 0x take a "huge jump", from ∞ for x < 0, to 1 at x = 0, to 0 for x > 0.[12] In 1814, Pfaff used a squeeze theorem argument to prove that xx → 1 as x → 0+.[8]

On the other hand, in 1821 Cauchy[18] explained why the limit of xy as positive numbers x and y approach 0 while being constrained by some fixed relation could be made to assume any value between 0 and ∞ by choosing the relation appropriately. He deduced that the limit of the full two-variable function xy without a specified constraint is "indeterminate". With this justification, he listed 00 along with expressions like ⁠0/0⁠ in a table of indeterminate forms.

Apparently unaware of Cauchy's work, Möbius[8] in 1834, building on Pfaff's argument, claimed incorrectly that f(x)g(x) → 1 whenever f(x),g(x) → 0 as x approaches a number c (presumably f is assumed positive away from c). Möbius reduced to the case c = 0, but then made the mistake of assuming that each of f and g could be expressed in the form Pxn for some continuous function P not vanishing at 0 and some nonnegative integer n, which is true for analytic functions, but not in general. An anonymous commentator pointed out the unjustified step;[19] then another commentator who signed his name simply as "S" provided the explicit counterexamples (e−1/x)x → e−1 and (e−1/x)2x → e−2 as x → 0+ and expressed the situation by writing that "00 can have many different values".[19]

Current situation

  • Some authors define 00 as 1 because it simplifies many theorem statements. According to Benson (1999), "The choice whether to define 00 is based on convenience, not on correctness. If we refrain from defining 00, then certain assertions become unnecessarily awkward. ... The consensus is to use the definition 00 = 1, although there are textbooks that refrain from defining 00."[20] Knuth (1992) contends more strongly that 00 "has to be 1"; he draws a distinction between the value 00, which should equal 1, and the limiting form 00 (an abbreviation for a limit of f(t)g(t) where f(t), g(t) → 0), which is an indeterminate form: "Both Cauchy and Libri were right, but Libri and his defenders did not understand why truth was on their side."[17]
  • Other authors leave 00 undefined because 00 is an indeterminate form: f(t), g(t) → 0 do not imply f(t)g(t) → 0.[21][22]

There do not seem to be any authors assigning 00 a specific value other than 1.[20]

Treatment on computers

IEEE floating-point standard

The IEEE 754-2008 floating-point standard is used in the design of most floating-point libraries. It recommends a number of operations for computing a power:[23]

  • pown (whose exponent is an integer) treats 00 as 1; see § Discrete exponents.
  • pow (whose intent is to return a non-NaN result when the exponent is an integer, like pown) treats 00 as 1.
  • powr treats 00 as NaN (Not-a-Number) due to the indeterminate form; see § Continuous exponents.

The pow variant is inspired by the pow function from C99, mainly for compatibility.[24] It is useful mostly for languages with a single power function. The pown and powr variants have been introduced due to conflicting usage of the power functions and the different points of view (as stated above).[25]

Programming languages

The C and C++ standards do not specify the result of 00 (a domain error may occur). But for C, as of C99, if the normative annex F is supported, the result for real floating-point types is required to be 1 because there are significant applications for which this value is more useful than NaN[26] (for instance, with discrete exponents); the result on complex types is not specified, even if the informative annex G is supported. The Java standard,[27] the .NET Framework method System.Math.Pow,[28] Julia, and Python[29][30] also treat 00 as 1. Some languages document that their exponentiation operation corresponds to the pow function from the C mathematical library; this is the case with Lua[31] and Perl's ** operator[32] (where it is explicitly mentioned that the result of 0**0 is platform-dependent).

Mathematical and scientific software

APL,[citation needed] R,[33] Stata, SageMath,[34] Matlab, Magma, GAP, Singular, PARI/GP,[35] and GNU Octave evaluate x0 to 1. Mathematica[36] and Macsyma simplify x0 to 1 even if no constraints are placed on x; however, if 00 is entered directly, it is treated as an error or indeterminate. SageMath does not simplify 0x. Maple, Mathematica[36] and PARI/GP[35][37] further distinguish between integer and floating-point values: If the exponent is a zero of integer type, they return a 1 of the type of the base; exponentiation with a floating-point exponent of value zero is treated as undefined, indeterminate or error.

References

  1. ^ Bourbaki, Nicolas (2004). "III.§3.5". Elements of Mathematics, Theory of Sets. Springer-Verlag.
  2. ^ Bourbaki, Nicolas (1970). "§III.2 No. 9". Algèbre. Springer. L'unique monôme de degré 0 est l'élément unité de A[(Xi)i∈I]; on l'identifie souvent à l'élément unité 1 de A
  3. ^ Bourbaki, Nicolas (1970). "§IV.1 No. 3". Algèbre. Springer.
  4. ^ Graham, Ronald; Knuth, Donald; Patashnik, Oren (1989-01-05). "Binomial coefficients". Concrete Mathematics (1st ed.). Addison-Wesley Longman Publishing Co. p. 162. ISBN 0-201-14236-8. Some textbooks leave the quantity 00 undefined, because the functions x0 and 0x have different limiting values when x decreases to 0. But this is a mistake. We must define x0 = 1, for all x, if the binomial theorem is to be valid when x = 0, y = 0, and/or x = −y. The binomial theorem is too important to be arbitrarily restricted! By contrast, the function 0x is quite unimportant.
  5. ^ Vaughn, Herbert E. (1970). "The expression 00". The Mathematics Teacher. 63: 111–112.
  6. ^ Malik, S. C.; Arora, Savita (1992). Mathematical Analysis. New York, USA: Wiley. p. 223. ISBN 978-81-224-0323-7. In general the limit of φ(x)/ψ(x) when x = a in case the limits of both the functions exist is equal to the limit of the numerator divided by the denominator. But what happens when both limits are zero? The division (0/0) then becomes meaningless. A case like this is known as an indeterminate form. Other such forms are ∞/∞, 0 × ∞, ∞ − ∞, 00, 1∞ and ∞0.
  7. ^ Paige, L. J. (March 1954). "A note on indeterminate forms". American Mathematical Monthly. 61 (3): 189–190. doi:10.2307/2307224. JSTOR 2307224.
  8. ^ a b c Möbius, A. F. (1834). "Beweis der Gleichung 00 = 1, nach J. F. Pfaff" [Proof of the equation 00 = 1, according to J. F. Pfaff]. Journal für die reine und angewandte Mathematik (in German). 1834 (12): 134–136. doi:10.1515/crll.1834.12.134. S2CID 199547186.
  9. ^ Carrier, George F.; Krook, Max; Pearson, Carl E. (2005). Functions of a Complex Variable: Theory and Technique. p. 15. ISBN 0-89871-595-4. Since log(0) does not exist, 0z is undefined. For Re(z) > 0, we define it arbitrarily as 0.
  10. ^ Gonzalez, Mario (1991). Classical Complex Analysis. Chapman & Hall. p. 56. ISBN 0-8247-8415-4. For z = 0, w ≠ 0, we define 0w = 0, while 00 is not defined.
  11. ^ Meyerson, Mark D. (June 1996). "The xx Spindle". Mathematics Magazine. Vol. 69, no. 3. pp. 198–206. doi:10.1080/0025570X.1996.11996428. ... Let's start at x = 0. Here xx is undefined.
  12. ^ a b Euler, Leonhard (1988). "Chapter 6, §97". Introduction to analysis of the infinite, Book 1. Translated by Blanton, J. D. Springer. p. p. 75. ISBN 978-0-387-96824-7. {{cite book}}: |page= has extra text (help)
  13. ^ Euler, Leonhard (1988). "Chapter 6, §99". Introduction to analysis of the infinite, Book 1. Translated by Blanton, J. D. Springer. p. p. 76. ISBN 978-0-387-96824-7. {{cite book}}: |page= has extra text (help)
  14. ^ a b Libri, Guillaume (1833). "Mémoire sur les fonctions discontinues". Journal für die reine und angewandte Mathematik (in French). 1833 (10): 303–316. doi:10.1515/crll.1833.10.303. S2CID 121610886.
  15. ^ Euler, Leonhard (1787). Institutiones calculi differentialis, Vol. 2. Ticini. ISBN 978-0-387-96824-7.
  16. ^ Libri, Guillaume (1830). "Note sur les valeurs de la fonction 00x". Journal für die reine und angewandte Mathematik (in French). 1830 (6): 67–72. doi:10.1515/crll.1830.6.67. S2CID 121706970.
  17. ^ a b Knuth, Donald E. (1992). "Two Notes on Notation". The American Mathematical Monthly. 99 (5): 403–422. arXiv:math/9205211. Bibcode:1992math......5211K. doi:10.1080/00029890.1992.11995869.
  18. ^ Cauchy, Augustin-Louis (1821), Cours d'Analyse de l'École Royale Polytechnique, Oeuvres Complètes: 2 (in French), vol. 3, pp. 65–69
  19. ^ a b Anonymous (1834). "Bemerkungen zu dem Aufsatze überschrieben "Beweis der Gleichung 00 = 1, nach J. F. Pfaff"" [Remarks on the essay "Proof of the equation 00 = 1, according to J. F. Pfaff"]. Journal für die reine und angewandte Mathematik (in German). 1834 (12): 292–294. doi:10.1515/crll.1834.12.292.
  20. ^ a b Benson, Donald C. (1999). Written at New York, USA. The Moment of Proof: Mathematical Epiphanies. Oxford, UK: Oxford University Press. p. 29. ISBN 978-0-19-511721-9.
  21. ^ Edwards; Penney (1994). Calculus (4th ed.). Prentice-Hall. p. 466.
  22. ^ Keedy; Bittinger; Smith (1982). Algebra Two. Addison-Wesley. p. 32.
  23. ^ Muller, Jean-Michel; Brisebarre, Nicolas; de Dinechin, Florent; Jeannerod, Claude-Pierre; Lefèvre, Vincent; Melquiond, Guillaume; Revol, Nathalie; Stehlé, Damien; Torres, Serge (2010). Handbook of Floating-Point Arithmetic (1 ed.). Birkhäuser. p. 216. doi:10.1007/978-0-8176-4705-6. ISBN 978-0-8176-4704-9. LCCN 2009939668. ISBN 978-0-8176-4705-6 (online), ISBN 0-8176-4704-X (print)
  24. ^ "More transcendental questions". grouper.ieee.org. Archived from the original on 2017-11-14. Retrieved 2019-05-27. (NB. Beginning of the discussion about the power functions for the revision of the IEEE 754 standard, May 2007.)
  25. ^ "Re: A vague specification". grouper.ieee.org. Archived from the original on 2017-11-14. Retrieved 2019-05-27. (NB. Suggestion of variants in the discussion about the power functions for the revision of the IEEE 754 standard, May 2007.)
  26. ^ Rationale for International Standard—Programming Languages—C (PDF) (Report). Revision 5.10. April 2003. p. 182.
  27. ^ "Math (Java Platform SE 8) pow". Oracle.
  28. ^ ".NET Framework Class Library Math.Pow Method". Microsoft.
  29. ^ "Built-in Types — Python 3.8.1 documentation". Retrieved 2020-01-25. Python defines pow(0, 0) and 0 ** 0 to be 1, as is common for programming languages.
  30. ^ "math — Mathematical functions — Python 3.8.1 documentation". Retrieved 2020-01-25. Exceptional cases follow Annex 'F' of the C99 standard as far as possible. In particular, pow(1.0, x) and pow(x, 0.0) always return 1.0, even when x is a zero or a NaN.
  31. ^ "Lua 5.3 Reference Manual". Retrieved 2019-05-27.
  32. ^ "perlop – Exponentiation". Retrieved 2019-05-27.
  33. ^ The R Core Team (2019-07-05). "R: A Language and Environment for Statistical Computing – Reference Index" (PDF). Version 3.6.1. p. 23. Retrieved 2019-11-22. 1 ^ y and y ^ 0 are 1, always.
  34. ^ The Sage Development Team (2020). "Sage 9.2 Reference Manual: Standard Commutative Rings. Elements of the ring Z of integers". Retrieved 2021-01-21. For consistency with Python and MPFR, 0^0 is defined to be 1 in Sage.
  35. ^ a b "pari.git / commitdiff – 10- x ^ t_FRAC: return an exact result if possible; e.g. 4^(1/2) is now 2". Retrieved 2018-09-10.
  36. ^ a b "Wolfram Language & System Documentation: Power". Wolfram. Retrieved 2018-08-02.
  37. ^ The PARI Group (2018). "Users' Guide to PARI/GP (version 2.11.0)" (PDF). pp. 10, 122. Retrieved 2018-09-04. There is also the exponentiation operator ^, when the exponent is of type integer; otherwise, it is considered as a transcendental function. ... If the exponent n is an integer, then exact operations are performed using binary (left-shift) powering techniques. ... If the exponent n is not an integer, powering is treated as the transcendental function exp(n log x).
Retrieved from "https://en.wikipedia.org/enwiki/w/index.php?title=Zero_to_the_power_of_zero&oldid=1038039428"