Abbe number: Difference between revisions
m v2.04b - Fix errors for CW project (Link equal to linktext) |
proper use of \text{} within TeX |
||
| Line 9: | Line 9: | ||
where ''n''<sub>C</sub>, ''n''<sub>D</sub> and ''n''<sub>F</sub> are the [[refractive indices]] of the material at the wavelengths of the [[Fraunhofer lines|Fraunhofer]] C, D<sub>1</sub>, and F [[spectral line]]s (656.3 [[nanometre|nm]], 589.3 nm, and 486.1 nm respectively). This formulation only applies to the [[visible spectrum]]. Outside this range requires the use of different spectral lines. For non-visible spectral lines the term V-number is more commonly used. The more general formulation defined as, |
where ''n''<sub>C</sub>, ''n''<sub>D</sub> and ''n''<sub>F</sub> are the [[refractive indices]] of the material at the wavelengths of the [[Fraunhofer lines|Fraunhofer]] C, D<sub>1</sub>, and F [[spectral line]]s (656.3 [[nanometre|nm]], 589.3 nm, and 486.1 nm respectively). This formulation only applies to the [[visible spectrum]]. Outside this range requires the use of different spectral lines. For non-visible spectral lines the term V-number is more commonly used. The more general formulation defined as, |
||
:<math>V = \frac{ n_{center} - 1 }{ n_{short} - n_{long} },</math> |
:<math>V = \frac{ n_\text{center} - 1 }{ n_\text{short} - n_\text{long} },</math> |
||
where ''n''<sub>short</sub>, ''n''<sub>center</sub> and ''n''<sub>long</sub> are the refractive indices of the material at three different wavelengths. The shortest wavelength index is ''n''<sub>short</sub> and the longest is ''n''<sub>long</sub>. |
where ''n''<sub>short</sub>, ''n''<sub>center</sub> and ''n''<sub>long</sub> are the refractive indices of the material at three different wavelengths. The shortest wavelength index is ''n''<sub>short</sub> and the longest is ''n''<sub>long</sub>. |
||
| Line 63: | Line 63: | ||
==Derivation== |
==Derivation== |
||
Starting from the [[Lens#Lensmaker's_equation|Lensmaker's equation]] for a '''thin''' lens {{cn|date=January 2021}} |
Starting from the [[Lens#Lensmaker's_equation|Lensmaker's equation]] for a '''thin''' lens {{cn|date=January 2021}} |
||
:<math> P=\frac{1}{f} = (n-1) \left[ \frac{1}{R_1} - \frac{1}{R_2} + \frac{(n-1)d}{n R_1 R_2} \right] \approx (n-1) \left( \frac{1}{R_1} - \frac{1}{R_2}\right) </math> |
:<math> P=\frac{1}{f} = (n-1) \left[ \frac{1}{R_1} - \frac{1}{R_2} + \frac{(n-1)d}{n R_1 R_2} \right] \approx (n-1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) </math> |
||
The change of [[refractive power]] ''P'' between the two wavelengths ''λ''<sub>short</sub> and ''λ''<sub>long</sub> is given by |
The change of [[refractive power]] ''P'' between the two wavelengths ''λ''<sub>short</sub> and ''λ''<sub>long</sub> is given by |
||
:<math>\delta P= P_{short}-P_{long}= (n_s-n_l) \left( \frac{1}{R_1} - \frac{1}{R_2}\right) </math> |
:<math>\delta P= P_\text{short}-P_\text{long}= (n_s-n_l) \left( \frac{1}{R_1} - \frac{1}{R_2}\right) </math> |
||
This is expressed in terms of the power ''P''<sub>c</sub> at ''λ''<sub>center</sub> by multiplying and dividing by <math>n_c-1</math> |
This is expressed in terms of the power ''P''<sub>c</sub> at ''λ''<sub>center</sub> by multiplying and dividing by <math>n_c-1</math> |
||
:<math>\delta P=\frac{ n_s-n_l }{ n_c - 1 } (n_c-1) \left( \frac{1}{R_1} - \frac{1}{R_2}\right)= \frac{ n_s-n_l }{ n_c - 1 } P_c = \frac{ P_c }{ V } </math> |
:<math>\delta P=\frac{ n_s-n_l }{ n_c - 1 } (n_c-1) \left( \frac{1}{R_1} - \frac{1}{R_2}\right)= \frac{ n_s-n_l }{ n_c - 1 } P_c = \frac{ P_c }{ V } </math> |
||
The relative change is '''inversely proportional''' to ''V'' |
The relative change is '''inversely proportional''' to ''V'' |
||
:<math> \frac{ \delta P }{ P_c }= \frac |
:<math> \frac{ \delta P }{ P_c }= \frac 1 V</math> |
||
==See also== |
==See also== |
||
Revision as of 17:42, 4 November 2021
In optics and lens design, the Abbe number, also known as the V-number or constringence of a transparent material, is an approximate measure of the material's dispersion (change of refractive index versus wavelength), with high values of V indicating low dispersion. It is named after Ernst Abbe (1840–1905), the German physicist who defined it. The term V-number should not be confused with the normalized frequency in fibers.
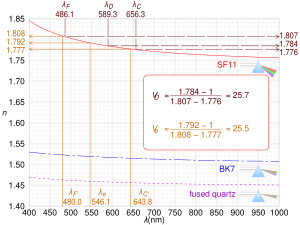
The Abbe number,[1][2] VD, of a material is defined as
where nC, nD and nF are the refractive indices of the material at the wavelengths of the Fraunhofer C, D1, and F spectral lines (656.3 nm, 589.3 nm, and 486.1 nm respectively). This formulation only applies to the visible spectrum. Outside this range requires the use of different spectral lines. For non-visible spectral lines the term V-number is more commonly used. The more general formulation defined as,
where nshort, ncenter and nlong are the refractive indices of the material at three different wavelengths. The shortest wavelength index is nshort and the longest is nlong.
Abbe numbers are used to classify glass and other optical materials in terms of their chromaticity. For example, the higher dispersion flint glasses have V < 55 whereas the lower dispersion crown glasses have larger Abbe numbers. Values of V range from below 25 for very dense flint glasses, around 34 for polycarbonate plastics, up to 65 for common crown glasses, and 75 to 85 for some fluorite and phosphate crown glasses.
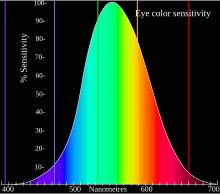
Abbe numbers are used in the design of achromatic lenses, as their reciprocal is proportional to dispersion (slope of refractive index versus wavelength) in the wavelength region where the human eye is most sensitive (see graph). For different wavelength regions, or for higher precision in characterizing a system's chromaticity (such as in the design of apochromats), the full dispersion relation (refractive index as a function of wavelength) is used.
Abbe diagram

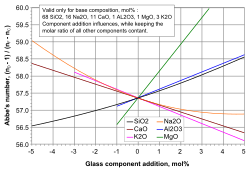
An Abbe diagram, also called 'the glass veil', is produced by plotting the Abbe number Vd of a material versus its refractive index nd. Glasses can then be categorised and selected according to their positions on the diagram. This can be a letter-number code, as used in the Schott Glass catalogue, or a 6-digit glass code.
Glasses' Abbe numbers, along with their mean refractive indices, are used in the calculation of the required refractive powers of the elements of achromatic lenses in order to cancel chromatic aberration to first order. Note that these two parameters which enter into the equations for design of achromatic doublets are exactly what is plotted on an Abbe diagram.
Due to the difficulty and inconvenience in producing sodium and hydrogen lines, alternate definitions of the Abbe number are often substituted (ISO 7944).[4] Rather than the standard definition, above, using the refractive index variation between the F and C hydrogen lines, an alternative measure using the subscript "e"
takes the difference between the refractive indices of the blue and red cadmium lines at 480.0 nm and 643.8 nm (with ne referring to the wavelength of the mercury e-line, 546.073 nm). Other definitions can similarly be employed; the following table lists standard wavelengths at which n is commonly determined, including the standard subscripts employed.[5]
| λ in nm | Fraunhofer's symbol | Light source | Color |
|---|---|---|---|
| 365.01 | i | Hg | UV-A |
| 404.66 | h | Hg | violet |
| 435.84 | g | Hg | blue |
| 479.99 | F' | Cd | blue |
| 486.13 | F | H | blue |
| 546.07 | e | Hg | green |
| 587.56 | d | He | yellow |
| 589.3 | D | Na | yellow |
| 643.85 | C' | Cd | red |
| 656.27 | C | H | red |
| 706.52 | r | He | red |
| 768.2 | A' | K | IR-A |
| 852.11 | s | Cs | IR-A |
| 1013.98 | t | Hg | IR-A |
Derivation
Starting from the Lensmaker's equation for a thin lens [citation needed]
The change of refractive power P between the two wavelengths λshort and λlong is given by
This is expressed in terms of the power Pc at λcenter by multiplying and dividing by
The relative change is inversely proportional to V
See also
- Abbe prism
- Abbe refractometer
- Calculation of glass properties, including Abbe number
- Glass code
- Sellmeier equation, more comprehensive and physically based modeling of dispersion
References
- ^ Hovestadt, H. (1902). Jena Glass and Its Scientific and Industrial Applications. London: Macmillan and Co. pp. 1–81.
- ^ Bergmann, Ludwig; Clemens Schaefer (1999). Optics of Waves and Particles. Berlin: Walter de Gruyter. pp. 198–201. ISBN 3-11-014318-6.
- ^ Abbe number calculation of glasses
- ^ Meister, Darryl. "Understanding Reference Wavelengths" (PDF). Carl Zeiss Vision. Retrieved 2013-03-13.
- ^ L. D. Pye, V. D. Frechette, N. J. Kreidl: "Borate Glasses"; Plenum Press, New York, 1977




![{\displaystyle P={\frac {1}{f}}=(n-1)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)d}{nR_{1}R_{2}}}\right]\approx (n-1)\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right)}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/33b2aafe756f52d290f91a90c43fc847dd76f2ed)



