Specular reflection: Difference between revisions
DRosenbach (talk | contribs) another example of specular reflection, notable in that it is on a man-made object |
DRosenbach (talk | contribs) change size |
||
| Line 1: | Line 1: | ||
[[Image:Reflection_angles.svg|frame|Diagram of specular reflection]] |
[[Image:Reflection_angles.svg|frame|Diagram of specular reflection]] |
||
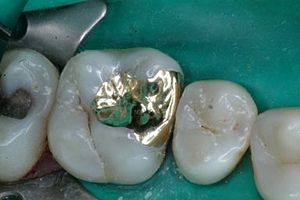
[[Image:MO inlay of 3.jpg| |
[[Image:MO inlay of 3.jpg|300px|right|Specular reflection on this [[Crown and bridge|gold inlay]].]] |
||
[[Image:Yuyuan Gardens - water reflection.JPG|thumb|right|Reflections on water are an example of specular reflection.]] |
[[Image:Yuyuan Gardens - water reflection.JPG|thumb|right|Reflections on water are an example of specular reflection.]] |
||
'''Specular reflection''' is the perfect, [[mirror]]-like [[reflection (physics)|reflection]] of light (or sometimes other kinds of [[wave]]) from a surface, in which light from a single incoming direction is reflected into a single outgoing direction. Such behaviour is described by the '''law of reflection''', which states that the direction of outgoing reflected light and the direction of incoming light make the same angle with respect to the [[surface normal]]; this is commonly stated as <math>\theta _i = \theta _r</math>. |
'''Specular reflection''' is the perfect, [[mirror]]-like [[reflection (physics)|reflection]] of light (or sometimes other kinds of [[wave]]) from a surface, in which light from a single incoming direction is reflected into a single outgoing direction. Such behaviour is described by the '''law of reflection''', which states that the direction of outgoing reflected light and the direction of incoming light make the same angle with respect to the [[surface normal]]; this is commonly stated as <math>\theta _i = \theta _r</math>. |
||
Revision as of 16:44, 18 March 2007


Specular reflection is the perfect, mirror-like reflection of light (or sometimes other kinds of wave) from a surface, in which light from a single incoming direction is reflected into a single outgoing direction. Such behaviour is described by the law of reflection, which states that the direction of outgoing reflected light and the direction of incoming light make the same angle with respect to the surface normal; this is commonly stated as .
This is in contrast to diffuse reflection, where incoming light is reflected in a broad range of directions. The most familiar example of the distinction between specular and diffuse reflection would be matte and glossy paints. While both exhibit a combination of specular and diffuse reflection, matte paints have a higher proportion of diffuse reflection and glossy paints have a greater proportion of specular reflection. Very highly polished surfaces, such as high quality mirrors, can exhibit almost perfect specular reflection.
Even when a surface exhibits only specular reflection with no diffuse reflection, not all of the light is necessarily reflected. Some of the light may be absorbed by the materials. Additionally, depending on the type of material behind the surface, some of the light may be transmitted through the surface. For most interfaces between materials, the fraction of the light that is reflected increases with increasing angle of incidence . If the light is propagating in a material with a higher index of refraction than the material whose surface it strikes, then total internal reflection may occur.
The law of reflection arises from diffraction of a plane wave (with small wavelength) on a flat boundary: when the boundary size is much larger than the wavelength then electrons of the boundary are seen oscillating exactly in phase only from one direction — the specular direction. If a mirror becomes very small (comparable to the wavelength), the law of reflection no longer holds and the behaviour of light is more complicated.


