Log-Cauchy distribution: Difference between revisions
m link [sS]pecies abundance |
→Characterization: All other formulas in the article distinguish the levels of parentheses according to American Physical Society style. |
||
| Line 39: | Line 39: | ||
For <math>\mu = 0</math> and <math>\sigma =1</math>, corresponding to a standard Cauchy distribution, the probability density function reduces to:<ref name=life/> |
For <math>\mu = 0</math> and <math>\sigma =1</math>, corresponding to a standard Cauchy distribution, the probability density function reduces to:<ref name=life/> |
||
:<math> f(x; 0,1) = \frac{1}{x\pi |
:<math> f(x; 0,1) = \frac{1}{x\pi [1 + (\ln x)^2]}, \ \ x>0</math> |
||
===Cumulative distribution function=== |
===Cumulative distribution function=== |
||
| Line 51: | Line 51: | ||
===Hazard rate=== |
===Hazard rate=== |
||
The [[hazard rate]] when <math>\mu = 0</math> and <math>\sigma =1</math> is:<ref name=life/> |
The [[hazard rate]] when <math>\mu = 0</math> and <math>\sigma =1</math> is:<ref name=life/> |
||
:<math> \lambda(x; 0,1) = \left |
:<math> \lambda(x; 0,1) = \left\{\frac{1}{x\pi \left[1 + \left(\ln x\right)^2\right]} \left[\frac{1}{2} - \frac{1}{\pi} \arctan(\ln x)\right]\right\}^{-1}, \ \ x>0</math> |
||
The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.<ref name=life/> |
The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.<ref name=life/> |
||
Latest revision as of 08:30, 26 June 2023
|
Probability density function 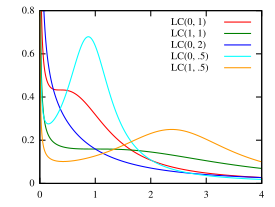 | |||
|
Cumulative distribution function 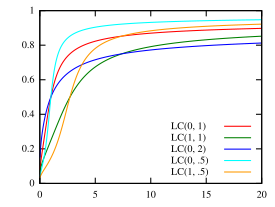 | |||
| Parameters |
(real) (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | infinite | ||
| Median | |||
| Variance | infinite | ||
| Skewness | does not exist | ||
| Excess kurtosis | does not exist | ||
| MGF | does not exist | ||
In probability theory, a log-Cauchy distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Cauchy distribution. If X is a random variable with a Cauchy distribution, then Y = exp(X) has a log-Cauchy distribution; likewise, if Y has a log-Cauchy distribution, then X = log(Y) has a Cauchy distribution.[1]
Characterization
[edit]The log-Cauchy distribution is a special case of the log-t distribution where the degrees of freedom parameter is equal to 1.[2]
Probability density function
[edit]The log-Cauchy distribution has the probability density function:
where is a real number and .[1][3] If is known, the scale parameter is .[1] and correspond to the location parameter and scale parameter of the associated Cauchy distribution.[1][4] Some authors define and as the location and scale parameters, respectively, of the log-Cauchy distribution.[4]
For and , corresponding to a standard Cauchy distribution, the probability density function reduces to:[5]
Cumulative distribution function
[edit]The cumulative distribution function (cdf) when and is:[5]
Survival function
[edit]The survival function when and is:[5]
Hazard rate
[edit]The hazard rate when and is:[5]
The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.[5]
Properties
[edit]The log-Cauchy distribution is an example of a heavy-tailed distribution.[6] Some authors regard it as a "super-heavy tailed" distribution, because it has a heavier tail than a Pareto distribution-type heavy tail, i.e., it has a logarithmically decaying tail.[6][7] As with the Cauchy distribution, none of the non-trivial moments of the log-Cauchy distribution are finite.[5] The mean is a moment so the log-Cauchy distribution does not have a defined mean or standard deviation.[8][9]
The log-Cauchy distribution is infinitely divisible for some parameters but not for others.[10] Like the lognormal distribution, log-t or log-Student distribution and Weibull distribution, the log-Cauchy distribution is a special case of the generalized beta distribution of the second kind.[11][12] The log-Cauchy is actually a special case of the log-t distribution, similar to the Cauchy distribution being a special case of the Student's t distribution with 1 degree of freedom.[13][14]
Since the Cauchy distribution is a stable distribution, the log-Cauchy distribution is a logstable distribution.[15] Logstable distributions have poles at x=0.[14]
Estimating parameters
[edit]The median of the natural logarithms of a sample is a robust estimator of .[1] The median absolute deviation of the natural logarithms of a sample is a robust estimator of .[1]
Uses
[edit]In Bayesian statistics, the log-Cauchy distribution can be used to approximate the improper Jeffreys-Haldane density, 1/k, which is sometimes suggested as the prior distribution for k where k is a positive parameter being estimated.[16][17] The log-Cauchy distribution can be used to model certain survival processes where significant outliers or extreme results may occur.[3][4][18] An example of a process where a log-Cauchy distribution may be an appropriate model is the time between someone becoming infected with HIV and showing symptoms of the disease, which may be very long for some people.[4] It has also been proposed as a model for species abundance patterns.[19]
References
[edit]- ^ a b c d e f Olive, D.J. (June 23, 2008). "Applied Robust Statistics" (PDF). Southern Illinois University. p. 86. Archived from the original (PDF) on September 28, 2011. Retrieved 2011-10-18.
- ^ Olosunde, Akinlolu & Olofintuade, Sylvester (January 2022). "Some Inferential Problems from Log Student's T-distribution and its Multivariate Extension". Revista Colombiana de Estadística - Applied Statistics. 45 (1): 209–229. doi:10.15446/rce.v45n1.90672. Retrieved 2022-04-01.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b Lindsey, J.K. (2004). Statistical analysis of stochastic processes in time. Cambridge University Press. pp. 33, 50, 56, 62, 145. ISBN 978-0-521-83741-5.
- ^ a b c d Mode, C.J. & Sleeman, C.K. (2000). Stochastic processes in epidemiology: HIV/AIDS, other infectious diseases. World Scientific. pp. 29–37. ISBN 978-981-02-4097-4.
- ^ a b c d e f Marshall, A.W. & Olkin, I. (2007). Life distributions: structure of nonparametric, semiparametric, and parametric families. Springer. pp. 443–444. ISBN 978-0-387-20333-1.
- ^ a b Falk, M.; Hüsler, J. & Reiss, R. (2010). Laws of Small Numbers: Extremes and Rare Events. Springer. p. 80. ISBN 978-3-0348-0008-2.
- ^ Alves, M.I.F.; de Haan, L. & Neves, C. (March 10, 2006). "Statistical inference for heavy and super-heavy tailed distributions" (PDF). Archived from the original (PDF) on June 23, 2007.
- ^ "Moment". Mathworld. Retrieved 2011-10-19.
- ^ Wang, Y. "Trade, Human Capital and Technology Spillovers: An Industry Level Analysis". Carleton University: 14.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Bondesson, L. (2003). "On the Lévy Measure of the Lognormal and LogCauchy Distributions". Methodology and Computing in Applied Probability: 243–256. Archived from the original on 2012-04-25. Retrieved 2011-10-18.
- ^ Knight, J. & Satchell, S. (2001). Return distributions in finance. Butterworth-Heinemann. p. 153. ISBN 978-0-7506-4751-9.
- ^ Kemp, M. (2009). Market consistency: model calibration in imperfect markets. Wiley. ISBN 978-0-470-77088-7.
- ^ MacDonald, J.B. (1981). "Measuring Income Inequality". In Taillie, C.; Patil, G.P.; Baldessari, B. (eds.). Statistical distributions in scientific work: proceedings of the NATO Advanced Study Institute. Springer. p. 169. ISBN 978-90-277-1334-6.
- ^ a b Kleiber, C. & Kotz, S. (2003). Statistical Size Distributions in Economics and Actuarial Science. Wiley. pp. 101–102, 110. ISBN 978-0-471-15064-0.
- ^ Panton, D.B. (May 1993). "Distribution function values for logstable distributions". Computers & Mathematics with Applications. 25 (9): 17–24. doi:10.1016/0898-1221(93)90128-I.
- ^ Good, I.J. (1983). Good thinking: the foundations of probability and its applications. University of Minnesota Press. p. 102. ISBN 978-0-8166-1142-3.
- ^ Chen, M. (2010). Frontiers of Statistical Decision Making and Bayesian Analysis. Springer. p. 12. ISBN 978-1-4419-6943-9.
- ^ Lindsey, J.K.; Jones, B. & Jarvis, P. (September 2001). "Some statistical issues in modelling pharmacokinetic data". Statistics in Medicine. 20 (17–18): 2775–278. doi:10.1002/sim.742. PMID 11523082. S2CID 41887351.
- ^ Zuo-Yun, Y.; et al. (June 2005). "LogCauchy, log-sech and lognormal distributions of species abundances in forest communities". Ecological Modelling. 184 (2–4): 329–340. doi:10.1016/j.ecolmodel.2004.10.011.




![{\displaystyle {1 \over x\pi }\left[{\sigma \over (\ln x-\mu )^{2}+\sigma ^{2}}\right],\ \ x>0}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/8ac7d87d9737a9d396f445dfeb9b4cff6c3d0a12)


![{\displaystyle {\begin{aligned}f(x;\mu ,\sigma )&={\frac {1}{x\pi \sigma \left[1+\left({\frac {\ln x-\mu }{\sigma }}\right)^{2}\right]}},\ \ x>0\\&={1 \over x\pi }\left[{\sigma \over (\ln x-\mu )^{2}+\sigma ^{2}}\right],\ \ x>0\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/a188fc444184e191f4e0325b64a2fb201546adfe)





![{\displaystyle f(x;0,1)={\frac {1}{x\pi [1+(\ln x)^{2}]}},\ \ x>0}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/c949bf99e759a9ba26dc5577f0925c93778fbc56)


![{\displaystyle \lambda (x;0,1)=\left\{{\frac {1}{x\pi \left[1+\left(\ln x\right)^{2}\right]}}\left[{\frac {1}{2}}-{\frac {1}{\pi }}\arctan(\ln x)\right]\right\}^{-1},\ \ x>0}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/517de41276551270538d7c0ed002e4419828ee45)