Abbe number

In optics and lens design, the Abbe number, also known as the V-number or constringence of a transparent material, is an approximate measure of the material's dispersion (change of refractive index versus wavelength), with high values of V indicating low dispersion. It is named after Ernst Abbe (1840–1905), the German physicist who defined it. The term V-number should not be confused with the normalized frequency in fibers.

Refractive index variation for SF11 flint glass, BK7 borosilicate crown glass, and fused quartz, and calculation for two Abbe numbers for SF11.

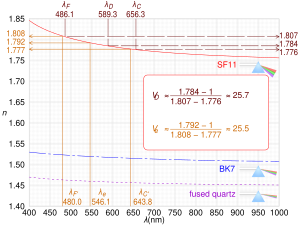
The Abbe number, V_d, of a material is defined as

$V_{D}={\frac {n_{d}-1}{n_{F}-n_{C}}},$

where n_C, n_d and n_F are the refractive indices of the material at the wavelengths of the Fraunhofer C, d, and F spectral lines (656.3 nm, 587.56 nm, and 486.1 nm respectively). This formulation only applies to the visible spectrum. Outside this range requires the use of different spectral lines. For non-visible spectral lines the term V-number is more commonly used. The more general formulation defined as,

$V={\frac {n_{\text{center}}-1}{n_{\text{short}}-n_{\text{long}}}},$

where n_short, n_center and n_long are the refractive indices of the material at three different wavelengths. The shortest wavelength index is n_short and the longest is n_long.

Abbe numbers are used to classify glass and other optical materials in terms of their chromaticity. For example, the higher dispersion flint glasses have V < 55 whereas the lower dispersion crown glasses have larger Abbe numbers. Values of V range from below 25 for very dense flint glasses, around 34 for polycarbonate plastics, up to 65 for common crown glasses, and 75 to 85 for some fluorite and phosphate crown glasses.

Most of the human eye's wavelength sensitivity curve, shown here, is bracketed by the Abbe number reference wavelengths of 486.1 nm (blue) and 656.3 nm (red)

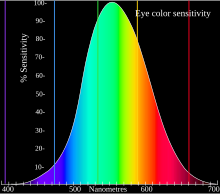
Abbe numbers are used in the design of achromatic lenses, as their reciprocal is proportional to dispersion (slope of refractive index versus wavelength) in the wavelength region where the human eye is most sensitive (see graph). For different wavelength regions, or for higher precision in characterizing a system's chromaticity (such as in the design of apochromats), the full dispersion relation (refractive index as a function of wavelength) is used.

Abbe diagram

An Abbe diagram, also known as 'the glass veil', plots the Abbe number against refractive index for a range of different glasses (red dots). Glasses are classified using the Schott Glass letter-number code to reflect their composition and position on the diagram.

Influences of selected glass component additions on the Abbe number of a specific base glass.

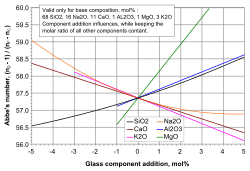
An Abbe diagram, also called 'the glass veil', is produced by plotting the Abbe number V_d of a material versus its refractive index n_d. Glasses can then be categorised and selected according to their positions on the diagram. This can be a letter-number code, as used in the Schott Glass catalogue, or a 6-digit glass code.

Glasses' Abbe numbers, along with their mean refractive indices, are used in the calculation of the required refractive powers of the elements of achromatic lenses in order to cancel chromatic aberration to first order. These two parameters which enter into the equations for design of achromatic doublets are exactly what is plotted on an Abbe diagram.

Due to the difficulty and inconvenience in producing sodium and hydrogen lines, alternate definitions of the Abbe number are often substituted (ISO 7944). Rather than the standard definition, above, using the refractive index variation between the F and C hydrogen lines, an alternative measure using the subscript "e"

$V_{e}={\frac {n_{e}-1}{n_{F'}-n_{C'}}}$

takes the difference between the refractive indices of the blue and red cadmium lines at 480.0 nm and 643.8 nm (with n_e referring to the wavelength of the mercury e-line, 546.073 nm). Other definitions can similarly be employed; the following table lists standard wavelengths at which n is commonly determined, including the standard subscripts employed.

λ in nm	Fraunhofer's symbol	Light source	Color
365.01	i	Hg	UV-A
404.66	h	Hg	violet
435.84	g	Hg	blue
479.99	F'	Cd	blue
486.13	F	H	blue
546.07	e	Hg	green
587.56	d	He	yellow
589.3	D	Na	yellow
643.85	C'	Cd	red
656.27	C	H	red
706.52	r	He	red
768.2	A'	K	IR-A
852.11	s	Cs	IR-A
1013.98	t	Hg	IR-A

Derivation

Starting from the Lensmaker's equation we obtain the thin lens equation:

$P={\frac {1}{\ f~}}=(n-1){\Biggl [}{\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}+{\frac {\ (n-1)\ d~}{\ n\ R_{1}R_{2}\ }}{\Biggr ]}\approx (n-1)\left({\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}\right)$

for $d\ll {\sqrt {\ R_{1}R_{2}\ }}~.$

The change of refractive power $\ P\$ between the two wavelengths $\ \lambda _{\mathsf {short}}\$ and $\ \lambda _{\mathsf {long}}\$ is given by

$\Delta P=P_{\mathsf {short}}-P_{\mathsf {\ \!long}}=(n_{\mathsf {s}}-n_{\mathsf {\ell }})\left({\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}\right)\ ,$

where $\ n_{\mathsf {s}}\$ and $\ n_{\mathsf {\ell }}\$ are the short and long wavelengths refractive indexes, respectively, and $\ n_{\mathsf {c}}\ ,$ below, is for the center.

The power difference is expressed in terms of the power

$\ P_{\mathsf {c}}\ =(n_{\mathsf {c}}-1)\left({\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}\right)$

at the center wavelength $\ \lambda _{\mathsf {center}}\$ by multiplying and dividing by $\ n_{\mathsf {c}}-1\$

$\Delta P=\left(n_{\mathsf {s}}-n_{\mathsf {\ell }}\right)\left({\frac {\ n_{\mathsf {c}}-1\ }{n_{\mathsf {c}}-1}}\right)\left({\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}\right)=\left({\frac {\ \ n_{\mathsf {s}}-n_{\mathsf {\ell }}\ }{n_{\mathsf {c}}-1}}\right)P_{\mathsf {c}}={\frac {\ P_{\mathsf {c}}\ }{V}}$

The relative change is inversely proportional to $\ V\$

${\frac {\ \Delta P\ }{P_{\mathsf {c}}}}={\frac {1}{\ V\ }}$

See also

• Abbe prism
• Abbe refractometer
• Calculation of glass properties, including Abbe number
• Glass code
• Sellmeier equation, more comprehensive and physically based modeling of dispersion

External links

• Abbe graph and data for 356 glasses from Ohara, Hoya, and Schott