Binary tree

In computer science, a binary tree is a tree data structure in which each node has at most two children. Typically the child nodes are called left and right. One common use of binary trees is binary search trees; another is binary heaps.

A simple binary tree of size 9 and height 3, with a root node whose value is 2

Definitions for rooted trees

• A directed edge refers to the link from the parent to the child (the arrows in the picture of the tree).
• The root node of a tree is the node with no parents. There is at most one root node in a rooted tree.
• A leaf is a node that has no children.
• The depth of a node n is the length of the path from the root to the node. The set of all nodes at a given depth is sometimes called a level of the tree. The root node is at depth zero.
• The height of a tree is the length of the path from the root node to its furthest leaf.
• Siblings are nodes that share the same parent node.
• If a path exists from node p to node q, where node p is closer to the root node than q, then p is an ancestor of q and q is a descendant of p.
• The size of a node is the number of descendants it has including itself.

Types of binary trees

• A rooted binary tree is a rooted tree in which every node has at most two children.
• A full binary tree, or proper binary tree, is a tree in which every node has zero or two children.
• A perfect binary tree (sometimes complete binary tree) is a full binary tree in which all leaves are at the same depth.
• A complete binary tree may also be defined as a full binary tree in which all leaves are at depth n or n-1 for some n. In order for a tree to be the latter kind of complete binary tree, all the children on the last level must occupy the leftmost spots consecutively, with no spot left unoccupied in between any two. For example, if two nodes on the bottommost level each occupy a spot with an empty spot between the two of them, but the rest of the children nodes are tightly wedged together with no spots in between, then the tree cannot be a complete binary tree due to the empty spot.
• A rooted complete binary tree can be identified with a free magma.
• An almost complete binary tree is a tree in which each node that has a right child also has a left child. Having a left child does not require a node to have a right child. Stated alternately, an almost complete binary tree is a tree where for a right child, there is always a left child, but for a left child there may not be a right child.
• The number of nodes n in a complete binary tree can be found using this formula: n = 2^(h+1)-1 where h is the height of the tree.
• The number of leaf nodes n in a complete binary tree can be found using this formula: n = 2^h where h is the height of the tree.

Definition in graph theory

Graph theorists use the following definition: A binary tree is a connected acyclic graph such that the degree of each vertex is no more than 3. It can be shown that in any binary tree, there are exactly two more nodes of degree one than there are of degree three, but there can be any number of nodes of degree two. A rooted binary tree is such a graph that has one of its vertices of degree no more than 2 singled out as the root.

With the root thus chosen, each vertex will have a uniquely defined parent, and up to two children; however, so far there is insufficient information to distinguish a left or right child. If we drop the connectedness requirement, allowing multiple connected components in the graph, we call such a structure a forest.

Another way of defining binary trees is a recursive definition on directed graphs. A binary tree is either:

• A single vertex.
• A graph formed by taking two binary trees, adding a vertex, and adding an edge directed from the new vertex to the root of each binary tree.

This also does not establish the order of children, but does fix a specific root node.

Combinatorics

Th groupings of pairs of nodes in a tree can be represented as pairs of letters, surrounded by parenthesis. Thus, (a b) denotes the binary tree whose left subtree is a and whose right subtree is b. Thus, strings of balanced pairs of parenthesis may be used denote binary trees in general. The set of all possible strings consisting entirely of balanced parenthesis is known as the Dyck language.

Given n+1 nodes, the total number of ways in which these nodes can be arranged into a binary tree is given by the Catalan number $C_{n}$. Thus, for example, $C_{2}=2$ is the statement that (ab)c and a(bc) are the only two binary trees possible, that have 3 nodes.

The ability to represent binary trees as strings of symbols and parentheses implies that binary trees can represent the elements of a magma. Conversely, the set of all possible binary trees, together with the natural operation of attaching trees to one-another, forms a magma, the free magma.

Given a string representing a binary tree, the operators to obtain the left and right subtrees are sometimes referred to as car and cdr.

Methods for storing binary trees

Binary trees can be constructed from programming language primitives in several ways. In a language with records and references, binary trees are typically constructed by having a tree node structure which contains some data and references to its left child and its right child. Sometimes it also contains a reference to its unique parent. If a node has fewer than two children, some of the child pointers may be set to a special null value, or to a special sentinel node.

Binary trees can also be stored as an implicit data structure in arrays, and if the tree is a complete binary tree, this method wastes no space. In this compact arrangement, if a node has an index i, its children are found at indices 2i+1 and 2i+2, while its parent (if any) is found at index floor((i-1)/2) (assuming the root has index zero). This method benefits from more compact storage and better locality of reference, particularly during a preorder traversal. However, it is expensive to grow and wastes space proportional to 2^h - n for a tree of height h with n nodes.

In languages with tagged unions such as ML, a tree node is often a tagged union of two types of nodes, one of which is a 3-tuple of data, left child, and right child, and the other of which is a "leaf" node, which contains no data and functions much like the null value in a language with pointers.

Methods of iterating over binary trees

Often, one wishes to visit each of the nodes in a tree and examine the value there. There are several common orders in which the nodes can be visited, and each has useful properties that are exploited in algorithms based on binary trees.

Pre-order, in-order, and post-order traversal.

Main article: Tree traversal.

Pre-order, in-order, and post-order traversal visit each node in a tree by recursively visiting each node in the left and right subtrees of the root. If the root node is visited before its subtrees, this is preorder; if after, postorder; if between, in-order. In-order traversal is useful in binary search trees, where this traversal visits the nodes in increasing order.

Depth-first order

In depth-first order, we always attempt to visit the node farthest from the root that we can, but with the caveat that it must be a child of a node we have already visited. Unlike a depth-first search on graphs, there is no need to remember all the nodes we have visited, because a tree cannot contain cycles. Pre-order, in-order, and post-order traversal are all special cases of this. See depth-first search for more information.

Breadth-first order

Contrasting with depth-first order is breadth-first order, which always attempts to visit the node closest to the root that it has not already visited. See Breadth-first search for more information.

Encodings

Succinct encodings

A succinct data structure is one which takes the absolute minimum possible space, as established by information theoretical lower bounds. The number of different binary trees on $n$ nodes is $\mathrm {C} _{n}$, the $n$th Catalan number (assuming we view trees with identical structure as identical). For large $n$, this is about $4^{n}$; thus we need at least about $\log _{2}4^{n}=2n$ bits to encode it. A succinct binary tree therefore would occupy only 2 bits per node.

One simple representation which meets this bound is to visit the nodes of the tree in preorder, outputting "1" for an internal node and "0" for a leaf. [1] If the tree contains data, we can simply simultaneously store it in a consecutive array in preorder. This function accomplishes this:

function EncodeSuccinct(node n, bitstring structure, array data) {
    if n = nil then
        append 0 to structure;
    else
        append 1 to structure;
        append n.data to data;
        EncodeSuccinct(n.left, structure, data);
        EncodeSuccinct(n.right, structure, data);
}

The string structure has only $2n+1$ bits in the end, where $n$ is the number of (internal) nodes; we don't even have to store its length. To show that no information is lost, we can convert the output back to the original tree like this:

function DecodeSuccinct(bitstring structure, array data) {
    remove first bit of structure and put it in b
    if b = 1 then
        create a new node n
        remove first element of data and put it in n.data
        n.left = DecodeSuccinct(structure, data)
        n.right = DecodeSuccinct(structure, data)
        return n
    else
        return nil
}

More sophisticated succinct representations allow not only compact storage of trees but even useful operations on those trees directly while they're still in their succinct form.

Encoding n-ary trees as binary trees

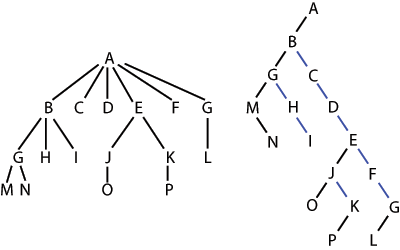
There is a one-to-one mapping between general ordered trees and binary trees, which in particular is used by Lisp to represent general ordered trees as binary trees. Each node N in the ordered tree corresponds to a node N' in the binary tree; the left child of N' is the node corresponding to the first child of N, and the right child of N' is the node corresponding to N 's next sibling --- that is, the next node in order among the children of the parent of N

One way of thinking about this is that each node's children are in a linked list, chained together with their right fields, and the node only has a pointer to the beginning or head of this list, through its left field.

For example, in the tree on the left, A has the 6 children {B,C,D,E,F,G}. It can be converted into the binary tree on the right.

The binary tree can be thought of as the original tree tilted sideways, with the black left edges representing first child and the blue right edges representing next sibling. The leaves of the tree on the left would be written in Lisp as:

(((M N) H I) C D ((O) (P)) F (L))

which would be implemented in memory as the binary tree on the right, without any letters on those nodes that have a left child.

See also

• AVL tree
• B-tree
• Binary search tree
• Binary space partitioning
• Red-black tree
• Threaded binary tree

References

• Donald Knuth. The art of computer programming vol 1. Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4. Section 2.3, especially subsections 2.3.1–2.3.2 (pp.318–348).

External Links

• NGenerics - implementation in C#