Cryptographic hash function: Difference between revisions
No edit summary |
Reverting possible vandalism by Special:Contributions/68.193.149.23 to version by CounterVandalismBot. If this is a mistake, report it. Thanks, ClueBot. (40631) (Bot) |
||
| Line 28: | Line 28: | ||
There is no formal definition which captures all of the properties considered desirable for a cryptographic hash function. These properties below are generally considered prerequisites: |
There is no formal definition which captures all of the properties considered desirable for a cryptographic hash function. These properties below are generally considered prerequisites: |
||
* ''[[preimage attack|Preimage resistant]]'' (See ''[[one way function]]'' for a related but slightly different property): given ''h'' it should be hard to find any ''m'' such that ''h'' = hash(''m''). |
* ''[[preimage attack|Preimage resistant]]'' (See ''[[one way function]]'' for a related but slightly different property): given ''h'' it should be hard to find any ''m'' such that ''h'' = hash(''m''). |
||
* ''[[preimage attack|Second preimage resistant]]'': given an input ''m''<sub>1</sub>, it should be hard |
* ''[[preimage attack|Second preimage resistant]]'': given an input ''m''<sub>1</sub>, it should be hard to find another input, ''m''<sub>2</sub> (not equal to ''m''<sub>1</sub>) such that |
||
:<math>hash(m_1)=hash(m_2).</math> |
|||
This property is implied by collision-resistance. Second preimage resistance is sometimes referred to as [[hash collision|weak collision resistance]]. |
This property is implied by collision-resistance. Second preimage resistance is sometimes referred to as [[hash collision|weak collision resistance]]. |
||
* ''[[collision attack|Collision-resistant]]'': it should be hard to find two different messages ''m''<sub>1</sub> and ''m''<sub>2</sub> such that hash(''m''<sub>1</sub>) = hash(''m''<sub>2</sub>). Due to a possible [[birthday attack]], this means the hash function output must be at least twice as large as what is required for preimage-resistance. This property is sometimes referred to as [[hash collision|strong collision resistance]]. |
* ''[[collision attack|Collision-resistant]]'': it should be hard to find two different messages ''m''<sub>1</sub> and ''m''<sub>2</sub> such that hash(''m''<sub>1</sub>) = hash(''m''<sub>2</sub>). Due to a possible [[birthday attack]], this means the hash function output must be at least twice as large as what is required for preimage-resistance. This property is sometimes referred to as [[hash collision|strong collision resistance]]. |
||
Revision as of 22:08, 25 October 2007
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. |
In cryptography, a cryptographic hash function is a transformation that takes an input and returns a fixed-size string, which is called the hash value. Hash functions with this property are used for a variety of computational purposes, including cryptography. The hash value is a concise representation of the longer message or document from which it was computed. The message digest is a sort of "digital fingerprint" of the larger document. Cryptographic hash functions are used to do message integrity checks and digital signatures in various information security applications, such as authentication and message integrity.
A hash function takes a long string (or 'message') of any length as input and produces a fixed length string as output, sometimes termed a message digest or a digital fingerprint. A hash value (also called a "digest" or a "checksum") is a kind of "signature" for a stream of data that represents the contents. One analogy that explains the role of the hash function would be the "tamper-evident" seals used on a software package.[1]
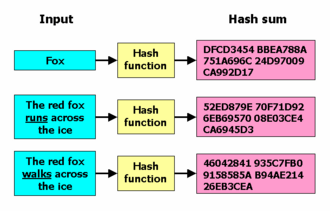
In various standards and applications, the two most-commonly used hash functions are MD5 and SHA-1. In 2005, security flaws were identified in both algorithms.
Overview
Broadly speaking, a cryptographic hash function should behave as much as possible like a random function while still being deterministic and efficiently computable.
A cryptographic hash function is considered insecure if either of the following is computationally feasible:
- finding a (previously unseen) message that matches a given digest
- finding "collisions", wherein two different messages have the same message digest.
An attacker who can do either of these things might, for example, use them to substitute an unauthorized message for an authorized one.
Ideally, it should not even be feasible to find two messages whose digests are substantially similar; nor would one want an attacker to be able to learn anything useful about a message given only its digest. Of course the attacker learns at least one piece of information, the digest itself, which for instance gives the attacker the ability to recognise the same message should it occur again.
Related algorithms
Checksums and cyclic redundancy checks (CRCs) are quite distinct from cryptographic hash functions, and are used for different applications. If used for security, they are vulnerable to attack; for example, a CRC was used for message integrity in the WEP encryption standard, but an attack was readily discovered which exploited the linearity of the checksum specified.
A message authentication code or MAC takes a message and a secret key and generates a "MAC tag", such that it is difficult for an attacker to generate a valid pair (message, tag) that doesn't match one they've already seen; they are used to prevent attackers forging messages, among other uses. Though it is sometimes referred to as a "keyed hash function", a MAC serves a very different purpose and has very different security properties than a cryptographic hash function; for example, it is not considered a flaw if it is easy for someone who knows the MAC key to generate two messages that have the same MAC. Hash functions can be used to create MAC functions; see for example HMAC.
Cryptographic properties
There is no formal definition which captures all of the properties considered desirable for a cryptographic hash function. These properties below are generally considered prerequisites:
- Preimage resistant (See one way function for a related but slightly different property): given h it should be hard to find any m such that h = hash(m).
- Second preimage resistant: given an input m1, it should be hard to find another input, m2 (not equal to m1) such that
This property is implied by collision-resistance. Second preimage resistance is sometimes referred to as weak collision resistance.
- Collision-resistant: it should be hard to find two different messages m1 and m2 such that hash(m1) = hash(m2). Due to a possible birthday attack, this means the hash function output must be at least twice as large as what is required for preimage-resistance. This property is sometimes referred to as strong collision resistance.
A hash function meeting these criteria may still have undesirable properties. For instance, many popular hash functions are vulnerable to length-extension attacks: given h(m) and len(m) but not m, by choosing a suitable m' an attacker can calculate h (m || m'), where || denotes concatenation. This property can be used to break naive authentication schemes based on hash functions. The HMAC construction works around these problems.
It is however, a common misconception that "one-wayness" of a cryptographic hash function means irreversibility of processing of the hash state, and that it somehow contradicts the principles used to construct block ciphers. Such "irreversibility" in fact means presence of local collisions that could facilitate attacks. The hash function must be a permutation processing its state bijectively to be cryptographically secure. It must be irreversible regarding the data block just like any block cipher must be irreversible regarding the key (it should be impossible to find the key that can encrypt a block A into a block B faster than the brute-force). This makes iterated block ciphers and hash functions processing blocks of the same size as secret keys of those block ciphers virtually identical, except the roles of key and data blocks are swapped. All the attacks against the MDx and SHA families of hash functions exploit local collisions in the processing of the data block. The local collisions caused by the final addition operation can also be exploited by these attacks.
Applications
A typical use of a cryptographic hash would be as follows: Alice poses a tough math problem to Bob, and claims she has solved it. Bob would like to try it himself, but would yet like to be sure that Alice is not bluffing. Therefore, Alice writes down her solution, appends a random nonce, computes its hash and tells Bob the hash value (whilst keeping the solution and nonce secret). This way, when Bob comes up with the solution himself a few days later, Alice can prove that she had the solution earlier by revealing the nonce to Bob. (This is an example of a simple commitment scheme; in actual practice, Alice and Bob will often be computer programs, and the secret would be something less easily spoofed than a claimed puzzle solution).
Another important application of secure hashes is verification of message integrity. Determination of whether or not any changes have been made to a message (or a file), for example, can be accomplished by comparing message digests calculated before, and after, transmission (or any other event).
A message digest can also serve as a means of reliably identifying a file; the Git source code management system uses the sha1sum of various types of content (file content, directory trees, ancestry information, etc) to uniquely identify them.
A related application is password verification. Passwords are usually not stored in cleartext, for obvious reasons, but instead in digest form. To authenticate a user, the password presented by the user is hashed and compared with the stored hash. This is sometimes referred to as one-way encryption.
For both security and performance reasons, most digital signature algorithms specify that only the digest of the message be "signed", not the entire message. Hash functions can also be used in the generation of pseudorandom bits.
SHA-1, MD5, and RIPEMD-160 are among the most commonly-used message digest algorithms as of 2005. In August 2004, researchers found weaknesses in a number of hash functions, including MD5, SHA-0 and RIPEMD. This has called into question the long-term security of later algorithms which are derived from these hash functions — in particular, SHA-1 (a strengthened version of SHA-0), RIPEMD-128, and RIPEMD-160 (both strengthened versions of RIPEMD). Neither SHA-0 nor RIPEMD are widely used since they were replaced by their strengthened versions. In February 2005, an attack on SHA-1 was reported, finding collisions in about 269 hashing operations, rather than the 280 expected for a 160-bit hash function. In August 2005, another attack on SHA-1 was reported, finding collisions in 263 operations.
Hashes are used to identify files on peer-to-peer filesharing networks. For example, in an ed2k link, a MD4-variant hash is combined with the file size, providing sufficient information for locating file sources, downloading the file and verifying its contents. [[Magnet: URI scheme|Magnet links]] are another example. Such file hashes are often the top hash of a hash list or a hash tree which allows for additional benefits.
Merkle-Damgård construction

A hash function must be able to process an arbitrary-length message into a fixed-length output. This can be achieved by breaking the input up into a series of equal-sized blocks, and operating on them in sequence using a one-way compression function. The compression function can either be specially designed for hashing or be built from a block cipher. A hash function built with the Merkle-Damgård construction is as resistant to collisions as is its compression function; any collision for the full hash function can be traced back to a collision in the compression function.
The last block processed should also be unambiguously length padded; this is crucial to the security of this construction. This construction is called the Merkle-Damgård construction. Most widely used hash functions, including SHA-1 and MD5, take this form.
Hash functions based on block ciphers
- Main article: One-way compression function
There are several methods to use a block cipher to build a cryptographic hash function. The methods resemble the block cipher modes of operation usually used for encryption.
Using a block cipher to build the one-way compression function for a hash function is usually much slower than using a specially designed one-way compression function in the hash function. But, in some cases it is easier because a single implementation of a block cipher can be used for both block cipher and a hash function. It can also save code space in very tiny embedded systems like for instance smart cards or nodes in cars or other machines.
In fact, all the existing hash functions are based either on block ciphers or on stream ciphers. MDx, SHA, Whirlpool, etc. can all be used as block ciphers without the final addition of the initial state to the output. Hash functions can be constructed based on stream ciphers as well (VEST), although certain properties are required for it to work - the stream cipher must be able to accept variable-length IVs and must process them bijectively.
Methods to make hash functions from block ciphers
See one-way compression function for details.
- Davies-Meyer
- Matyas-Meyer-Oseas
- Miyaguchi-Preneel
- MDC-2
- MDC-4
Use in building other cryptographic primitives
Hash functions can be used to build other cryptographic primitives. For these other primitives to be cryptographically secure care has to be taken to build them the right way.
Message authentication codes (MACs) are often built from hash functions. HMAC is such a MAC.
Just as block ciphers can be used to build hash functions, hash functions can be used to build block ciphers. Examples of such block ciphers are SHACAL, BEAR and LION.
Pseudorandom number generators (PRNGs) can be built using hash functions. This is done by combining a (secret) random seed with a counter and hashing it. If the counter is a bignum (allowed to count to any size) then the PRNG can have an infinite period.
Stream ciphers can be built using hash functions. Often this is done by first building a cryptographically secure pseudorandom number generator and then using its stream of random bytes as keystream and XOR that onto the cleartext to get the ciphertext. SEAL is such a stream cipher which is based on SHA-1.
Concatenation of cryptographic hash functions
Concatening multiple hash functions could produce a new hash function that is more secure than its component parts.[2] For example, one might concatenate the output of SHA-1 and RIPEMD-160 to produce a new function H(x) = SHA-1(x) || RIPEMD-160(x).
However, the new function is still no more secure than each of its component parts in isolation. Joux [3] noted that the iterative nature of cryptographic hash functions introduces a weakness. n-collisions (n different messages that hash to the same value) are effectively no more difficult to find than 2-collisions. If an n-collision can be found for RIPEMD, it is likely that amongst the n different messages there will be a collision in SHA-1. The time needed to find the SHA-1 collision is polynomial. This argument is summarized by Finney.
Concatenated hash functions are used within SSL and the Debian Advanced Packaging Tool system, both of which currently use concatenated MD5 and SHA-1 sums. This does not increase security, but provides redundancy in case one is broken: a valid reason for using multiple hash functions.
List of cryptographic hash functions
Some of the following algorithms are known to be insecure; consult the article for each specific algorithm for more information on the status of each algorithm. For even more hash functions see the box at the bottom of the page.
| Algorithm | Output size | Internal state size | Block size | Length size | Word size | Collision |
|---|---|---|---|---|---|---|
| HAVAL | 256/224/192/160/128 | 256 | 1024 | 64 | 32 | Yes |
| MD2 | 128 | 384 | 128 | No | 8 | Almost |
| MD4 | 128 | 128 | 512 | 64 | 32 | Yes |
| MD5 | 128 | 128 | 512 | 64 | 32 | Yes |
| PANAMA | 256 | 8736 | 256 | No | 32 | With flaws |
| RadioGatún | Arbitrarily long | 58 words | 3 words | No | 1-64 | No |
| RIPEMD | 128 | 128 | 512 | 64 | 32 | Yes |
| RIPEMD-128/256 | 128/256 | 128/256 | 512 | 64 | 32 | No |
| RIPEMD-160/320 | 160/320 | 160/320 | 512 | 64 | 32 | No |
| SHA-0 | 160 | 160 | 512 | 64 | 32 | Yes |
| SHA-1 | 160 | 160 | 512 | 64 | 32 | With flaws |
| SHA-256/224 | 256/224 | 256 | 512 | 64 | 32 | No |
| SHA-512/384 | 512/384 | 512 | 1024 | 128 | 64 | No |
| Tiger(2)-192/160/128 | 192/160/128 | 192 | 512 | 64 | 64 | No |
| VEST-4/8 (hash mode) | 160/256 | 256/384 | 8 | 80/128 | 1 | No[4] |
| VEST-16/32 (hash mode) | 320/512 | 512/768 | 8 | 160/256 | 1 | No |
| WHIRLPOOL | 512 | 512 | 512 | 256 | 8 | No |
The SHA hash functions are a series of functions developed by the NSA: SHA, also known as SHA-0, SHA-1 and four flavours of a function known as SHA-2.
Note: The internal state here means the "internal hash sum" after each compression of a data block. Most hash algorithms also internally use some additional variables such as length of the data compressed so far since that is needed for the length padding in the end. See the Merkle-Damgård construction for details.
See also
- Avalanche effect
- MD5CRK
- Message authentication code
- Keyed-hash message authentication code
- CRHF - Collision Resistant Hash Functions.
- UOWHF - Universal One Way Hash Functions.
- CRYPTREC and NESSIE - Projects which recommend hash functions.
- PGP word list
References
- ^ http://www.unixwiz.net/techtips/iguide-crypto-hashes.html
- ^ [1] suggested
- ^ Joux, Antoine. Multicollisions in Iterated Hash Functions. Application to Cascaded Constructions. LNCS 3152/2004, pages 306-316 Full text.
- ^ A. Joux and J-R. Reinhard, "Overtaking VEST" describes an attack that breaks ProVEST with a typo in the counter diffusor responsible for local collisions. VEST ciphers do not have that collision and therefore are not affected by this attack.
External links
- The Hash function lounge — a list of hash functions and known attacks
- Hash functions: Theory, attacks, and applications — a survey by Ilya Mironov (Microsoft Research)
- Helger Lipmaa's links on hash functions
- Diagrams explaining cryptographic hash functions
- An Illustrated Guide to Cryptographic Hashes by Steve Friedl
- Cryptanalysis of MD5 and SHA: Time for a New Standard by Bruce Schneier
- Hash collision Q&A
- Attacking hash functions by poisoned messages (construction of multiple sensible Postscript messages with the same hash function)
- What is a hash function? from RSA Laboratories
- Password Hashing in PHP by James McGlinn at the PHP Security Consortium

