Electric field

In physics, the space surrounding an electric charge or in the presence of a time-varying magnetic field has a property called an electric field. This electric field exerts a force on other electrically charged objects. The concept of electric field was introduced by Michael Faraday.

The electric field is a vector field with SI units of newtons per coulomb (N C⁻¹) or, equivalently, volts per meter (V m⁻¹). The direction of the field at a point is defined by the direction of the electric force exerted on a positive test charge placed at that point. The strength of the field is defined by the ratio of the electric force on a charge at a point to the magnitude of the charge placed at that point. Electric fields contain electrical energy with energy density proportional to the square of the field intensity. The electric field is to charge as acceleration is to mass and force density is to volume.

A moving charge has not just an electric field but also a magnetic field, and in general the electric and magnetic fields are not completely separate phenomena; what one observer perceives as an electric field, another observer in a different frame of reference perceives as a mixture of electric and magnetic fields. For this reason, one speaks of "electromagnetism" or "electromagnetic fields." In quantum mechanics, disturbances in the electromagnetic fields are called photons, and the energy of photons is quantized.

Coulomb's law

The electric field surrounding a point charge is given by Coulomb's law:

$\mathbf {E} ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r^{2}}}\mathbf {\hat {r}} \qquad {\mbox{(1)}}$

where

Q is the charge of the particle creating the electric field,

r is the distance from the particle with charge Q to the E-field evaluation point,

$\mathbf {\hat {r}}$ is the Unit vector pointing from the particle with charge Q to the E-field evaluation point,

$\varepsilon _{0}$ is the vacuum permittivity.

Coulomb's law is actually a special case of Gauss's Law, a more fundamental description of the relationship between the distribution of electric charge in space and the resulting electric field. Gauss's law is one of Maxwell's equations, a set of four laws governing electromagnetics.

Properties (in electrostatics)

Illustration of the electric field surrounding a positive (red) and a negative (green) charge.

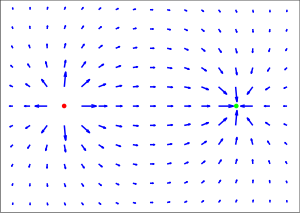
According to equation (1) above, electric field is dependent on position. The electric field due to any single charge falls off as the square of the distance from that charge.

Electric fields follow the superposition principle. If more than one charge is present, the total electric field at any point is equal to the vector sum of the respective electric fields that each object would create in the absence of the others.

$\mathbf {E} _{\rm {total}}=\sum _{i}\mathbf {E} _{i}=\mathbf {E} _{1}+\mathbf {E} _{2}+\mathbf {E} _{3}\ldots \,\!$

If this principle is extended to an infinite number of infinitesimally small elements of charge, the following formula results:

$\mathbf {E} ={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\rho }{r^{2}}}\mathbf {\hat {r}} \,\mathrm {d} V$

where

$\rho$ is the charge density, or the amount of charge per unit volume.

The electric field at a point is equal to the negative gradient of the electric potential there. In symbols,

$\mathbf {E} =-\mathbf {\nabla } \phi$

where

$\phi (x,y,z)$ is the scalar field representing the electric potential at a given point.

If several spatially distributed charges generate such an electric potential, e.g. in a solid, an electric field gradient may also be defined.

Considering the permittivity $\varepsilon$ of a material, which may differ from the permittivity of free space $\varepsilon _{0}$, the electric displacement field is:

$\mathbf {D} =\varepsilon \mathbf {E}$

Energy in the electric field

Main article: Electrical energy

The electric field stores energy. The energy density of the electric field is given by

$u={\frac {1}{2}}\varepsilon |\mathbf {E} |^{2}$

where

$\varepsilon$ is the permittivity of the medium in which the field exists

$\mathbf {E}$ is the electric field vector.

The total energy stored in the electric field in a given volume V is therefore

$\int _{V}{\frac {1}{2}}\varepsilon |\mathbf {E} |^{2}\,\mathrm {d} V$

where

$\mathrm {d} V$ is the differential volume element.

Parallels between electrostatics and gravity

Coulomb's law, which describes the interaction of electric charges:

$\mathbf {F} ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Qq}{r^{2}}}\mathbf {\hat {r}} =q\mathbf {E}$

is similar to the Newtonian gravitation law:

$\mathbf {F} =G{\frac {Mm}{r^{2}}}\mathbf {\hat {r}} =m\mathbf {g}$

This suggests similarities between the electric field $E$ and the gravitational field $g$, so sometimes mass is called "gravitational charge".

Similarities between electrostatic and gravitational forces:

1. Both act in a vacuum.
2. Both are central and conservative.
3. Both obey an inverse-square law (both are inversely proprotional to square of r).
4. Both propagate with finite speed c.

Differences between electrostatic and gravitational forces:

1. Electrostatic forces are much greater than gravitational forces (by about 10³⁶ times).
2. Gravitational forces are attractive for like charges, whereas electrostatic forces are repulsive for like charges.
3. There are no negative gravitational charges (no negative mass) while there are both positive and negative electric charges. This difference combined with previous implies that gravitational forces are always attractive, while electrostatic forces may be either attractive or repulsive.
4. Electric charges are invariant under Lorentz transformations while gravitational charges (relativistic mass) are not.

Time-varying fields

Charges do not only produce electric fields. As they move, they generate magnetic fields, and if the magnetic field changes, it generates electric fields. This "secondary" electric field can be computed using Faraday's law of induction,

$\mathbf {\nabla } \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$

where

$\mathbf {\nabla } \times \mathbf {E}$ indicates the curl of the electric field,

$-{\frac {\partial \mathbf {B} }{\partial t}}$ represents the vector rate of decrease of magnetic field with time.

This means that a magnetic field changing in time produces a curled electric field, possibly also changing in time. The situation in which electric or magnetic fields change in time is no longer electrostatics, but rather electrodynamics or electromagnetics.

See also

• Electrostatics
• Electrodynamics
• Maxwell's equations are the full set of equations governing electric fields.
• Magnetism
• Teltron Tube

External links

• Fields - a chapter from an online textbook
• Learning by Simulations Interactive simulation of an electric field of up to four point charges
• Java simulations of electrostatics in 2-D and 3-D