Monoid (category theory)

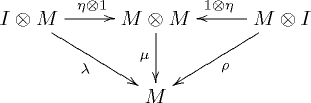
In category theory, a monoid (or monoid object) $(M,\mu ,\eta )$ in a monoidal category C is an object M together with two morphisms

• $\mu :M\otimes M\to M$ called multiplication,
• and $\eta :I\to M$ called unit,

such that the diagrams

and

commute. In the above notations, I is the unit element and $\alpha$, $\lambda$ and $\rho$ are respectively the associativity, the left identity and the right identity of the monoidal category C.

Dually, a comonoid in a monoidal category C is a monoid in the dual category $\mathbf {C} ^{\mathrm {op} }$.

Suppose that the monoidal category C has a symmetry $\gamma$. A monoid $M$ in C is symmetric when

$\mu \circ \gamma =\mu$.

Examples

• A monoid object in Set (with the monoidal structure induced by the cartesian product) is a monoid in the usual sense.
• A monoid object in Top (with the monoidal structure induced by the product topology) is a topological monoid.
• A monoid object in the category of monoids (with the direct product of monoids) is just a commutative monoid. This follows easily from the Eckmann–Hilton theorem.
• A monoid object in the category of complete join-semilattices Sup (with the monoidal structure induced by the cartesian product) is a unital quantale.
• A monoid object in (Ab, ⊗_Z, Z) is a ring.
• For a commutative ring R, a monoid object in (R-Mod, ⊗_R, R) is an R-algebra.
• A monoid object in K-Vect (again, with the tensor product) is a K-algebra, a comonoid object is a K-coalgebra.
• For any category C, the category [C,C] of its endofunctors has a monoidal structure induced by the composition. A monoid object in [C,C] is a monad on C.

Categories of monoids

Given two monoids $(M,\mu ,\eta )$ and $(M',\mu ',\eta ')$ in a monoidal category C, a morphism $f:M\to M'$ is a morphism of monoids when

• $f\circ \mu =\mu '\circ (f\otimes f)$,
• $f\circ \eta =\eta '$.

The category of monoids in C and their monoid morphisms is written $\mathbf {Mon} _{\mathbf {C} }$.

See also

• monoid (non-categorical definition)
• Act-S, the category of monoids acting on sets

References

• Mati Kilp, Ulrich Knauer, Alexander V. Mikhalov, Monoids, Acts and Categories (2000), Walter de Gruyter, Berlin ISBN 3-11-015248-7