Lambert W function

The graph of W₀(x) for −1/e ≤ x ≤ 4

In mathematics, The Lambert W function, named after Johann Heinrich Lambert, also called the Omega function or product log, is the inverse function of f(w) = we^w where e^w is the natural exponential function and w is any complex number. We will denote the function here by W. For every complex number z, we have

$z=W(z)e^{W(z)}.$

Since the function f is not injective in (−∞, 0), the function W is multivalued in [−1/e, 0). If we restrict to real arguments x ≥ −1/e and demand w ≥ −1, then a single-valued function W₀(x) is defined, whose graph is shown. We have W₀(0) = 0 and W₀(−1/e) = −1.

The Lambert W function cannot be expressed in terms of elementary functions. It is useful in combinatorics, for instance in the enumeration of trees. It can be used to solve various equations involving exponentials and also occurs in the solution of time-delayed differential equations, such as y'(t) = a y(t − 1).

Differential equation

By implicit differentiation, one can show that W satisfies the differential equation

$z(1+W){\frac {dW}{dz}}=W\quad \mathrm {for\ } z\neq -1/e.$

Taylor series

The Taylor series of W₀ around 0 can be found using the Lagrange inversion theorem and is given by

$W_{0}(x)=\sum _{n=1}^{\infty }{\frac {(-n)^{n-1}}{n!}}\ x^{n}=x-x^{2}+{\frac {3}{2}}x^{3}-{\frac {8}{3}}x^{4}+{\frac {125}{24}}x^{5}-\cdots$

The radius of convergence is 1/e, as may be seen by the ratio test. The function defined by this series can be extended to a holomorphic function defined on all complex numbers with a branch cut along the interval (−∞, −1/e]; this holomorphic function defines the principal branch of the Lambert W function.

Applications

Many equations involving exponentials can be solved using the W function. The general strategy is to move all instances of the unknown to one side of the equation and make it look like Y = Xe^X at which point the W function provides the solution.

In other words :

$X=Ye^{Y}\;\Longleftrightarrow \;Y=W(X)$

Examples

Example 1

$2^{t}=5t\,$

$\Rightarrow 1={\frac {5t}{2^{t}}}\,$

$\Rightarrow 1=5t\,e^{-t\ln 2}\,$

$\Rightarrow {\frac {1}{5}}=t\,e^{-t\ln 2}\,$

$\Rightarrow {\frac {-\,\ln 2}{5}}=(-\,t\,\ln 2)\,e^{(-t\ln 2)}\,$

$\Rightarrow -t\ln 2=W\left({\frac {-\ln 2}{5}}\right)\,$

$\Rightarrow t={\frac {-W\left({\frac {-\ln 2}{5}}\right)}{\ln 2}}\,$

More generally, the equation

$p^{ax+b}=cx+d$

where

$p>0\land c,d\neq 0$

can be transformed via the substitution

$-t=ax+{\frac {ad}{c}}$

into

$tp^{t}=R=-{\frac {a}{c}}p^{b-{\frac {ad}{c}}}$

giving

$t={\frac {W(R\ln p)}{\ln p}}$

which yields the final solution

$x=-{\frac {W(-{\frac {a\ln p}{c}}\,p^{b-{\frac {ad}{c}}})}{a\ln p}}-{\frac {d}{c}}$

Example 2

Similar techniques show that

$x^{x}=z$

has solution

$x={\frac {\ln(z)}{W(\ln z)}}$

or, equivalently,

$x=\exp \left(W(\ln(z))\right).$

Example 3

Whenever the complex infinite exponential

$z^{z^{z^{\cdots }}}\!$

converges, the Lambert W function provides the actual limit value as

$c={\frac {W(-\ln(z))}{-\ln(z)}}$

where ln(z) denotes the principal branch of the complex log function.

Example 4

Solutions for

$x\log _{b}\left(x\right)=a$

have the form

$x={\frac {a\ln(b)}{W(a\ln(b))}}$

Example 5

The solution for the current in a series diode/resistor circuit can also be written in terms of the Lambert W. See diode modeling.

Example 6

The delay differential equation

${\dot {y}}(t)=ay(t-1)$

has characteristic equation $\lambda =ae^{-\lambda }$, leading to $\lambda =W_{k}(a)$ and $y(t)=e^{W_{k}(a)t}$, where $k$ is the branch index. If $a$ is real, only $W_{0}(a)$ need be considered.

Integration

The function W(x), and many expressions involving W(x), can be integrated using the substitution w = W(x), i.e. x = w e^w:

$\int W(x)\,dx=x\left(W(x)-1+{\frac {1}{W(x)}}\right)+C$

Special values

$W\left(-{\frac {\pi }{2}}\right)={\frac {i\pi }{2}}$

$W\left(-{\frac {\ln 2}{2}}\right)=-\ln 2$

$W\left(-{1 \over e}\right)=-1$

$W(0)=0\,$

$W(1)=\Omega \,$ (the Omega constant)

$W(e)=1\,$

Plots

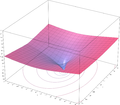
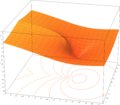
• Plots of the LambertW function on the complex plane
• 
  z = Re(W₀(x + i y))
• 
  z = Im(W₀(x + i y))
• 
• 

Evaluation algorithm

The W function may be evaluated using the recurrence relation

$w_{j+1}=w_{j}-{\frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}(w_{j}+1)-{\frac {(w_{j}+2)(w_{j}e^{w_{j}}-z)}{2w_{j}+2}}}}$

given in Corless et al. to compute W. Together with the evaluation error estimate given in Chapeau-Belandeau and Monir, the following Python code implements this:

import math
 
def lambertW(x, prec = 1E-12, maxiters = 100):
    w = 0
    for i in range(maxiters):
        we = w * pow(math.e,w)
        w1e = (w + 1) * pow(math.e,w)
        if prec > abs((x - we) / w1e):
            return w
        w -= (we - x) / (w1e - (w+2) * (we-x) / (2*w+2))
    raise ValueError("W doesn't converge fast enough for abs(z) = %f" % abs(x))

This computes the principal branch for $x>1/e$. It could be improved by giving better initial estimates.

The following closed form approximation may be used by itself when less accuracy is needed, or to give an excellent initial estimate to the above code, which then may need only a few iterations:

double
desy_lambert_W(double x) {
      double  lx1;
      if (x <= 500.0) {
              lx1 = ln(x + 1.0);
              return 0.665 * (1 + 0.0195 * lx1) * lx1 + 0.04;
      }
      return ln(x - 4.0) - (1.0 - 1.0/ln(x)) * ln(ln(x));
}

(from http://www.desy.de/~t00fri/qcdins/texhtml/lambertw/)

History

The Lambert W function has an unusual history: although its study dates back to a 1779 paper by Leonhard Euler, the inverse of we^w was not recognized as a function worthy of attention in its own right until the 1980s. The recognition came with the function's implementation in the Maple computer algebra system, for which purpose the name Lambert W was introduced. Lambert's name was chosen instead of Euler's because Euler referenced earlier work by Lambert in his paper, and possibly because "naming yet another function after Euler would not be useful" (Corless et al.).

References and external links

• Corless et al. Notes about Lambert W research
• Corless et al. "On the Lambert W function" Adv. Computational Maths. 5, 329 - 359 (1996) (PDF)
• Chapeau-Blondeau, F. and Monir, A: "Evaluation of the Lambert W Function and Application to Generation of Generalized Gaussian Noise With Exponent 1/2", IEEE Trans. Signal Processing, 50(9), 2002
• MathWorld - Lambert W-Function
• Lambert function from Wolfram's function site.
• Francis et al. "Quantitative General Theory for Periodic Breathing" Circulation 102 (18): 2214. (2000). Use of Lambert function to solve delay-differential dynamics in human disease.
• Extreme Mathematics. Monographs on the Lambert W function, its numerical approximation and generalizations for W-like inverses of transcendental forms with repeated exponential towers.
• Computing the Lambert Wfunction
• Why W?