Butterfly diagram

Data-flow diagram connecting the inputs x (left) to the outputs y that depend on them (right) for a "butterfly" step of a radix-2 Cooley-Tukey FFT. This diagram resembles a butterfly (as in the Morpho butterfly shown for comparison), hence the name.

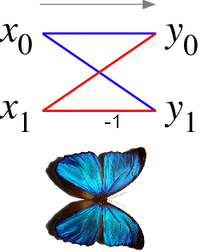
In the context of fast Fourier transform algorithms, a butterfly is a portion of the computation that combines the results of smaller discrete Fourier transforms (DFTs) into a larger DFT, or vice versa (breaking a larger DFT up into subtransforms). The name "butterfly" comes from the shape of the data-flow diagram in the radix-2 case, as described below.

Most commonly, the term "butterfly" appears in the context of the Cooley-Tukey FFT algorithm, which recursively breaks down a DFT of composite size $n=rm$ into $r$ smaller transforms of size $m$ where $r$ is the "radix" of the transform. These smaller DFTs are then combined with a size-$r$ butterflies, which themselves are DFTs of size $r$ (performed $m$ times on corresponding outputs of the sub-transforms) pre-multiplied by roots of unity (known as "twiddle factors"). (This is the "decimation in time" case; one can also perform the steps in reverse, known as "decimation in frequency", where the butterflies comes first and are post-multiplied by twiddle factors. See also the Cooley-Tukey FFT article.)

In the case of the radix-2 Cooley-Tukey algorithm, the butterfly is simply a DFT of size 2 that takes two inputs $(x_{0},x_{1})$ (corresponding outputs of the two sub-transforms) and gives two outputs $(y_{0},y_{1})$ by the formula (not including twiddle factors):

$y_{0}=x_{0}+x_{1}$

$y_{1}=x_{0}-x_{1}$

If one draws the data-flow diagram for this pair of operations, the $(x_{0},x_{1})$ to $(y_{0},y_{1})$ lines cross and resemble somewhat the wings of a butterfly, hence the name. (See also the illustration at right.)