Pappus graph: Difference between revisions
Appearance
Content deleted Content added
No edit summary |
automorphism group |
||
| Line 12: | Line 12: | ||
[[Image:Pappus graph colored.svg|thumb|250px|Pappus graph colored to show various circuits.]] |
[[Image:Pappus graph colored.svg|thumb|250px|Pappus graph colored to show various circuits.]] |
||
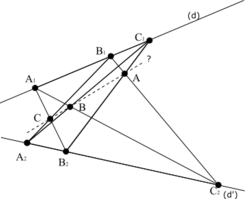
In the [[mathematics|mathematical]] field of [[graph theory]], the '''Pappus graph''' is a 3-[[regular graph]] with 18 vertices and 27 edges, formed as the [[Levi graph]] of the [[Pappus configuration]]. It is a [[distance-regular graph]], one of only 14 such [[cubic graph]]s according to [http://www.csse.uwa.edu.au/~gordon/remote/foster/#drgs Cubic symmetric graphs (The Foster Census)]. It has [[crossing number]] 5, and is the smallest cubic graph with that crossing number {{OEIS|id=A110507}}. |
In the [[mathematics|mathematical]] field of [[graph theory]], the '''Pappus graph''' is a 3-[[regular graph]] with 18 vertices and 27 edges, formed as the [[Levi graph]] of the [[Pappus configuration]]. It is a [[distance-regular graph]], one of only 14 such [[cubic graph]]s according to [http://www.csse.uwa.edu.au/~gordon/remote/foster/#drgs Cubic symmetric graphs (The Foster Census)]. It has [[crossing number]] 5, and is the smallest cubic graph with that crossing number {{OEIS|id=A110507}}. Its automorphism group has order 216. |
||
The name "Pappus graph" has also been used to refer to a related nine-vertex graph (Kagno 1947). |
The name "Pappus graph" has also been used to refer to a related nine-vertex graph (Kagno 1947). |
||
Revision as of 04:01, 26 January 2009
| Pappus graph | |
|---|---|
 The Pappus graph, a Levi graph with 18 vertices formed from the Pappus configuration. | |
| Named after | Pappus of Alexandria |
| Vertices | 18 |
| Edges | 27 |
| Properties | Distance-regular Cubic |
| Table of graphs and parameters | |

In the mathematical field of graph theory, the Pappus graph is a 3-regular graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is a distance-regular graph, one of only 14 such cubic graphs according to Cubic symmetric graphs (The Foster Census). It has crossing number 5, and is the smallest cubic graph with that crossing number (sequence A110507 in the OEIS). Its automorphism group has order 216.
The name "Pappus graph" has also been used to refer to a related nine-vertex graph (Kagno 1947).
References
- Kagno, I. N. (1947), "Desargues' and Pappus' graphs and their groups", American Journal of Mathematics, 69 (4): 859–863, doi:10.2307/2371806
