Fractal: Difference between revisions
m Reverted edits by 81.142.80.234 (talk) to last version by Erkan Yilmaz |
No edit summary |
||
| Line 206: | Line 206: | ||
{{Link FA|uk}} |
{{Link FA|uk}} |
||
[[af:Fraktaalmeetkunde]] |
|||
[[als:Fraktal]] |
[[als:Fraktal]] |
||
[[ar:هندسة كسيرية]] |
[[ar:هندسة كسيرية]] |
||
Revision as of 23:08, 8 May 2009

A fractal is generally "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole,"[1] a property called self-similarity. The term was coined by Benoît Mandelbrot in 1975 and was derived from the Latin fractus meaning "broken" or "fractured." A mathematical fractal is based on an equation that undergoes iteration, a form of feedback based on recursion.[2]
A fractal often has the following features:[3]
- It has a fine structure at arbitrarily small scales.
- It is too irregular to be easily described in traditional Euclidean geometric language.
- It is self-similar (at least approximately or stochastically).
- It has a Hausdorff dimension which is greater than its topological dimension (although this requirement is not met by space-filling curves such as the Hilbert curve).[4]
- It has a simple and recursive definition.
Because they appear similar at all levels of magnification, fractals are often considered to be infinitely complex (in informal terms). Natural objects that approximate fractals to a degree include clouds, mountain ranges, lightning bolts, coastlines, and snow flakes. However, not all self-similar objects are fractals—for example, the real line (a straight Euclidean line) is formally self-similar but fails to have other fractal characteristics; for instance, it is regular enough to be described in Euclidean terms.
Images of fractals can be created using fractal generating software. Images produced by such software are normally referred to as being fractals even if they do not have the above characteristics, as it is possible to zoom into a region of the image that does not exhibit any fractal properties.
History


The mathematics behind fractals began to take shape in the 17th century when mathematician and philosopher Leibniz considered recursive self-similarity (although he made the mistake of thinking that only the straight line was self-similar in this sense).
It took until 1872 before a function appeared whose graph would today be considered fractal, when Karl Weierstrass gave an example of a function with the non-intuitive property of being everywhere continuous but nowhere differentiable. In 1904, Helge von Koch, dissatisfied with Weierstrass's very abstract and analytic definition, gave a more geometric definition of a similar function, which is now called the Koch curve. (The image at right is three Koch curves put together to form what is commonly called the Koch snowflake.) In 1915, Waclaw Sierpinski constructed his triangle and, one year later, his carpet. Originally these geometric fractals were described as curves rather than the 2D shapes that they are known as in their modern constructions. In 1918, Bertrand Russell recognised a "supreme beauty" within the emerging mathematics of fractals.[2] The idea of self-similar curves was taken further by Paul Pierre Lévy, who, in his 1938 paper Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole described a new fractal curve, the Lévy C curve. Georg Cantor also gave examples of subsets of the real line with unusual properties—these Cantor sets are also now recognized as fractals.
Iterated functions in the complex plane were investigated in the late 19th and early 20th centuries by Henri Poincaré, Felix Klein, Pierre Fatou and Gaston Julia. However, without the aid of modern computer graphics, they lacked the means to visualize the beauty of many of the objects that they had discovered.
In the 1960s, Benoît Mandelbrot started investigating self-similarity in papers such as How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension, which built on earlier work by Lewis Fry Richardson. Finally, in 1975 Mandelbrot coined the word "fractal" to denote an object whose Hausdorff-Besicovitch dimension is greater than its topological dimension. He illustrated this mathematical definition with striking computer-constructed visualizations. These images captured the popular imagination; many of them were based on recursion, leading to the popular meaning of the term "fractal".
Examples

A class of examples is given by the Cantor sets, Sierpinski triangle and carpet, Menger sponge, dragon curve, space-filling curve, and Koch curve. Additional examples of fractals include the Lyapunov fractal and the limit sets of Kleinian groups. Fractals can be deterministic (all the above) or stochastic (that is, non-deterministic). For example, the trajectories of the Brownian motion in the plane have a Hausdorff dimension of 2.
Chaotic dynamical systems are sometimes associated with fractals. Objects in the phase space of a dynamical system can be fractals (see attractor). Objects in the parameter space for a family of systems may be fractal as well. An interesting example is the Mandelbrot set. This set contains whole discs, so it has a Hausdorff dimension equal to its topological dimension of 2—but what is truly surprising is that the boundary of the Mandelbrot set also has a Hausdorff dimension of 2 (while the topological dimension of 1), a result proved by Mitsuhiro Shishikura in 1991. A closely related fractal is the Julia set.
Generating fractals

|

|

|
 Even 2000 times magnification of the Mandelbrot set uncovers fine detail resembling the full set. Even 2000 times magnification of the Mandelbrot set uncovers fine detail resembling the full set. |
Four common techniques for generating fractals are:
- Escape-time fractals – (also known as "orbits" fractals) These are defined by a formula or recurrence relation at each point in a space (such as the complex plane). Examples of this type are the Mandelbrot set, Julia set, the Burning Ship fractal, the Nova fractal and the Lyapunov fractal. The 2d vector fields that are generated by one or two iterations of escape-time formulae also give rise to a fractal form when points (or pixel data) are passed through this field repeatedly.
- Iterated function systems – These have a fixed geometric replacement rule. Cantor set, Sierpinski carpet, Sierpinski gasket, Peano curve, Koch snowflake, Harter-Highway dragon curve, T-Square, Menger sponge, are some examples of such fractals.
- Random fractals – Generated by stochastic rather than deterministic processes, for example, trajectories of the Brownian motion, Lévy flight, fractal landscapes and the Brownian tree. The latter yields so-called mass- or dendritic fractals, for example, diffusion-limited aggregation or reaction-limited aggregation clusters.
- Strange attractors – Generated by iteration of a map or the solution of a system of initial-value differential equations that exhibit chaos.
Classification
Fractals can also be classified according to their self-similarity. There are three types of self-similarity found in fractals:
- Exact self-similarity – This is the strongest type of self-similarity; the fractal appears identical at different scales. Fractals defined by iterated function systems often display exact self-similarity.
- Quasi-self-similarity – This is a loose form of self-similarity; the fractal appears approximately (but not exactly) identical at different scales. Quasi-self-similar fractals contain small copies of the entire fractal in distorted and degenerate forms. Fractals defined by recurrence relations are usually quasi-self-similar but not exactly self-similar.
- Statistical self-similarity – This is the weakest type of self-similarity; the fractal has numerical or statistical measures which are preserved across scales. Most reasonable definitions of "fractal" trivially imply some form of statistical self-similarity. (Fractal dimension itself is a numerical measure which is preserved across scales.) Random fractals are examples of fractals which are statistically self-similar, but neither exactly nor quasi-self-similar.
In nature
Approximate fractals are easily found in nature. These objects display self-similar structure over an extended, but finite, scale range. Examples include clouds, snow flakes, crystals, mountain ranges, lightning, river networks, cauliflower or broccoli, and systems of blood vessels and pulmonary vessels. Coastlines may be loosely considered fractal in nature.
Trees and ferns are fractal in nature and can be modeled on a computer by using a recursive algorithm. This recursive nature is obvious in these examples—a branch from a tree or a frond from a fern is a miniature replica of the whole: not identical, but similar in nature. The connection between fractals and leaves are currently being used to determine how much carbon is contained in trees. This connection is hoped to help determine and solve the environmental issue of carbon emission and control. [5]
In 1999, certain self similar fractal shapes were shown to have a property of "frequency invariance"—the same electromagnetic properties no matter what the frequency—from Maxwell's equations (see fractal antenna).[6]
- widths="200px"
-
A fractal that models the surface of a mountain (animation)
-
A fractal fern computed using an Iterated function system
-
Photograph of a romanesco broccoli, showing a naturally occuring fractal
In creative works
Fractal patterns have been found in the paintings of American artist Jackson Pollock. While Pollock's paintings appear to be composed of chaotic dripping and splattering, computer analysis has found fractal patterns in his work.[7]
Decalcomania, a technique used by artists such as Max Ernst, can produce fractal-like patterns.[8] It involves pressing paint between two surfaces and pulling them apart.
Fractals are also prevalent in African art and architecture. Circular houses appear in circles of circles, rectangular houses in rectangles of rectangles, and so on. Such scaling patterns can also be found in African textiles, sculpture, and even cornrow hairstyles.[9]
- widths="200px"
-
A fractal is formed when pulling apart two glue-covered acrylic sheets.
-
High voltage breakdown within a 4″ block of acrylic creates a fractal Lichtenberg figure.
-
Romanesco broccoli showing very fine natural fractals
-
A "woodburn" fractal
-
A magnification of the phoenix set
-
Pascal generated fractal
-
A fractal flame created with the program Apophysis
-
Fractal made by the program Sterling
-
A fractal created using the program Apophysis and a julian transform
Applications
As described above, random fractals can be used to describe many highly irregular real-world objects. Other applications of fractals include:[11]
- Classification of histopathology slides in medicine
- Fractal landscape or Coastline complexity
- Enzyme/enzymology (Michaelis-Menten kinetics)
- Generation of new music
- Generation of various art forms
- Signal and image compression
- Creation of digital photographic enlargements
- Seismology
- Fractal in soil mechanics
- Computer and video game design, especially computer graphics for organic environments and as part of procedural generation
- Fractography and fracture mechanics
- Fractal antennas – Small size antennas using fractal shapes
- Small angle scattering theory of fractally rough systems
- T-shirts and other fashion
- Generation of patterns for camouflage, such as MARPAT
- Digital sundial
- Technical analysis of price series (see Elliott wave principle)
See also
- Bifurcation theory
- Butterfly effect
- Chaos theory
- Complexity
- Constructal theory
- Contraction mapping theorem
- Diamond-square algorithm
- Droste effect
- Feigenbaum function
- Fractal art
- Fractal compression
- Fractal cosmology
- Fractal flame
- Fractals in wikimedia
- Fractal landscape
- Fractint
- Fracton
- Graftal
- Greeble
- Lacunarity
- List of fractals by Hausdorff dimension
- Publications in fractal geometry
- Newton fractal
- Recursionism
- Sacred geometry
- Self-reference
- Space-filling curve
- Strange loop
- Turbulence
References
- ^ Mandelbrot, B.B. (1982). The Fractal Geometry of Nature. W.H. Freeman and Company. ISBN 0-7167-1186-9.
- ^ a b Briggs, John (1994). Fractals:The Patterns of Chaos. Thames and Hudson. p. 148. ISBN 0500276935.
{{cite book}}: Cite has empty unknown parameter:|coauthors=(help) - ^ Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd. xxv. ISBN 0-470-84862-6.
{{cite book}}: Unknown parameter|nopp=ignored (|no-pp=suggested) (help) - ^ The Hilbert curve map is not a homeomorhpism, so it does not preserve topological dimension. The topological dimension and Hausdorff dimension of the image of the Hilbert map in R2 are both 2. Note, however, that the topological dimension of the graph of the Hilbert map (a set in R3) is 1.
- ^ "Hunting the Hidden Dimension." Nova. PBS. WPMB-Maryland. 10/28/2008.
- ^ Hohlfeld,R., and Cohen, N.,"SELF-SIMILARITY AND THE GEOMETRIC REQUIREMENTS FOR FREQUENCY INDEPENDENCE IN ANTENNAE ", Fractals, Vol. 7, No. 1 (1999) 79-84
- ^ Richard Taylor, Adam P. Micolich and David Jonas. Fractal Expressionism : Can Science Be Used To Further Our Understanding Of Art?
- ^ A Panorama of Fractals and Their Uses by Michael Frame and Benoît B. Mandelbrot
- ^ Ron Eglash. African Fractals: Modern Computing and Indigenous Design. New Brunswick: Rutgers University Press 1999.
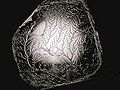
- ^ Peng, Gongwen (21 July 1990). "The fractal nature of a fracture surface". Journal of Physics A. 23 (14): 3257–3261. doi:10.1088/0305-4470/23/14/022. Retrieved 2007-06-02.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ "Applications". Retrieved 2007-10-21.
Further reading
- Barnsley, Michael F., and Hawley Rising. Fractals Everywhere. Boston: Academic Press Professional, 1993. ISBN 0-12-079061-0
- Falconer, Kenneth. Techniques in Fractal Geometry. John Willey and Sons, 1997. ISBN 0-471-92287-0
- Jürgens, Hartmut, Heins-Otto Peitgen, and Dietmar Saupe. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992. ISBN 0-387-97903-4
- Benoît B. Mandelbrot The Fractal Geometry of Nature. New York: W. H. Freeman and Co., 1982. ISBN 0-7167-1186-9
- Peitgen, Heinz-Otto, and Dietmar Saupe, eds. The Science of Fractal Images. New York: Springer-Verlag, 1988. ISBN 0-387-96608-0
- Clifford A. Pickover, ed. Chaos and Fractals: A Computer Graphical Journey - A 10 Year Compilation of Advanced Research. Elsevier, 1998. ISBN 0-444-50002-2
- Jesse Jones, Fractals for the Macintosh, Waite Group Press, Corte Madera, CA, 1993. ISBN 1-878739-46-8.
- Hans Lauwerier, Fractals: Endlessly Repeated Geometrical Figures, Translated by Sophia Gill-Hoffstadt, Princeton University Press, Princeton NJ, 1991. ISBN 0-691-08551-X, cloth. ISBN 0-691-02445-6 paperback. "This book has been written for a wide audience..." Includes sample BASIC programs in an appendix.
- Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850839-5 and ISBN 978-0-19-850839-7.
{{cite book}}: Check|isbn=value: invalid character (help) - Bernt Wahl, Peter Van Roy, Michael Larsen, and Eric Kampman Exploring Fractals on the Macintosh, Addison Wesley, 1995. ISBN 0-201-62630-6
- Nigel Lesmoir-Gordon. "The Colours of Infinity: The Beauty, The Power and the Sense of Fractals." ISBN 1-904555-05-5 (The book comes with a related DVD of the Arthur C. Clarke documentary introduction to the fractal concept and the Mandelbrot set.
- Gouyet, Jean-François. Physics and Fractal Structures (Foreword by B. Mandelbrot); Masson, 1996. ISBN 2-225-85130-1, and New York: Springer-Verlag, 1996. ISBN 0-387-94153-1. Out-of-print. Available in PDF version at [1].






![Fractal branching occurs in a fractured surface such as a microwave-irradiated DVD.[10]](/upwiki/wikipedia/commons/thumb/3/3c/Microwaved-DVD.jpg/120px-Microwaved-DVD.jpg)







