Pentomino

A pentomino is a polyomino composed of five (Greek πέντε / pente) congruent squares, connected orthogonally.

There are twelve different pentominoes, and they are named after letters of the alphabet. (The mirror image of a pentomino does not count as a different pentomino.)

If you allow mirror images to count as different pentominos, this brings the total to 18. The ones lettered T, V, I, X, U, and W have mirror images that are equivalent after rotation. This matters in some computer games, where mirror image moves are not allowed, such as Tetris-clones and Rampart. The F-pentomino is often referred to as the R-pentomino as well, notably in reference to Conway's Game of Life.

Considering rotations of multiples of 90 degrees only, we have the following symmetry categories:

• L, N, P, F and Y can be oriented in 8 ways: 4 by rotation, and 4 more for the mirror image.
• Z can be oriented in 4 ways: 2 by rotation, and 2 more for the mirror image.
• T, V, U and W can be oriented in 4 ways by rotation.
• I can be oriented in 2 ways by rotation.
• X can be oriented in only one way.

For 2D figures in general there is one more category: being orientable in 2 ways, which are each other's mirror image, for example a swastika. There is no pentomino in this category (this type of symmetry requires at least an octomino).

For example, the eight possible orientations of the Y pentomino are as follows:

File:Y pentomino.png

Tiling rectangles

Example tilings

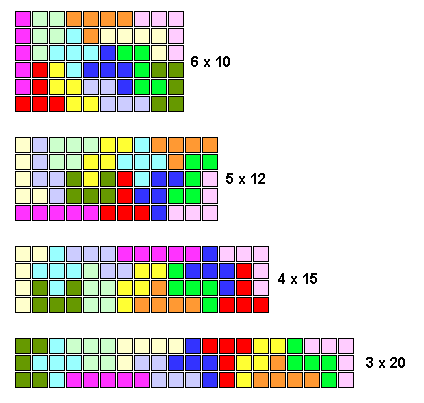
A standard pentomino puzzle is to tile a rectangular box with the pentominoes, i.e. cover it without overlap and without gaps. Each of the 12 pentominoes has an area of 5 unit squares, so the box must have an area of 60 units. Possible sizes are 6×10, 5×12, 4×15 and 3×20. The avid puzzler can probably solve these problems by hand within a few hours. A more challenging task, typically requiring a computer search, is to count the total number of solutions in each case.

The 6×10 case was first solved in 1965 by John Fletcher^[1]. There are exactly 2339 solutions, excluding trivial variations obtained by rotation and reflection of the whole rectangle, but including rotation and reflection of a subset of pentominoes (sometimes this is possible and provides in a simple way an additional solution; e.g., with the 3×20 solution shown, the other one is obtained by rotating a set of seven pentominoes, or put differently, by rotating the four leftmost and the rightmost to the other side).

The 5×12 box has 1010 solutions, the 4×15 box has 368 solutions, and the 3×20 box has just 2 solutions.

A somewhat easier (more symmetrical) puzzle, the 8×8 rectangle with a 2×2 hole in the center, was solved by Dana Scott as far back as 1958^[2]. There are 65 solutions. Scott's algorithm was one of the first applications of a backtracking computer program ever.

Efficient algorithms have been described to solve such problems, for instance by Donald Knuth^[3]. Running on modern hardware, these pentomino puzzles can now be solved in mere seconds.

Filling boxes

Another standard, yet far more enjoyable, pentomino puzzle is to fill a 3 dementional box with the pentominoes, i.e. cover it without overlap and without gaps. Each of the 12 pentominoes has a space of 5 unit cubes, so the box must have a volume of 60 units. Possible sizes are 2×5×6 and 3×4×5. Following are two of solutions.

2 x 5 x 6 box

 P P P N N N   P P L L L L  
 Y W N N X U   F F L Z Z U  
 Y W W X X X   V F F Z T U  
 Y Y W W X U   V F Z Z T U  
 Y I I I I I   V V V T T T  

3 x 4 x 5 box

 F F V V V   X F F P T   U F U P P   U U U P P  
 X N N N V   X L T T T   X L L L L   I I I I I  
 N N Z Z V   X W W Z T   W W Y Z Z   W Y Y Y Y  

Trivia

Pentominoes are prominently featured in a subplot of the novel Imperial Earth by Arthur C. Clarke.

"Pentominoes" was registered as a trademark by Solomon W. Golomb (#1008964 USPTO 1975 April 15), but this trademark is no longer in effect as of 1982.

Board game

There is a board game of skill based entirely on pentominoes, called pentominoes.

The game is played on an 8×8 grid by two or three players. Players take turns in placing pentominoes on the board so that they do not overlap with existing tiles and no tile is used more than once. The objective is to be the last player to place a tile on the board.

The two-player version has been weakly solved; it is a first-player win.

Pentominoes, and similar shapes, are also the basis of a number of other tiling games, patterns and puzzles. For example, a french board game called Blokus is played with 4 opposing color sets of polyominoes. In Blokus, each color begins with every pentomino (12), as well as every tetromino (5), ever tromino (2), every domino (1) , and every monomino (1). Like the game Pentominoes, the goal is to use all of your tiles, and a bonus is given if the monomino is saved for the very last move. The player with the least pieces remaining wins.

Video game

Tetris was inspired by pentomino puzzles.

See also

• Tiling puzzle
• Sudoku variants

References

• ^ John G. Fletcher (1965). "A program to solve the pentomino problem by the recursive use of macros". Communications of the ACM 8, 621–623.
• ^ Donald E. Knuth. "Dancing links" (Postscript, 1.6 megabytes). Includes a summary of Scott's and Fletcher's articles.
• ^ Dana S. Scott (1958). "Programming a combinatorial puzzle". Technical Report No. 1, Department of Electrical Engineering, Princeton University.

External links

• Pentominos Puzzle Solver featuring a Java applet that solves the 8x8 square with 4 holes.
• Fast Pentomino Solver by Bruce Hoyt, written in Forth using generated macros.
• Pentomino Relationships looks at families of pentomino puzzle solutions.
• Pentominoes as the origin of Tetris
• Pentomino.nl, a Shockwave pentomino game (in Dutch and English) with solutions database.