Transport length: Difference between revisions
TimothyRias (talk | contribs) m quick fix some layout issues |
No edit summary |
||
| Line 10: | Line 10: | ||
Image:figure_mean_free_path.png|Mean free path simple scheme |
Image:figure_mean_free_path.png|Mean free path simple scheme |
||
</gallery> |
</gallery> |
||
==External links== |
|||
* [http://www.formulaction.com/tech_mls_gb.html Illustrated description (movies) of multiple light scattering and application to colloid stability] |
|||
==References== |
==References== |
||
Revision as of 09:56, 11 September 2009
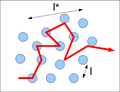
The transport length in a strongly diffusing medium (noted l*) is the length over which the direction of propagation of the photon is randomized. It is related to the mean free path l by the relation[1] :
with:
g: the assymetry coefficient. or averaging of the scattering angle θ over a high number of scattering events.
g can be evaluated with the Mie theory.
If g=0, l=l*. A single scattering is already isotropic.
If g→1, l*→infinite. A single scattering doesn't deviate the photons. Then the scattering never gets isotropic.
This length is usefull for renormalizing a non isotropic scattering problem into an isotropic one in order to use classical diffusion laws (Fick_law, Brownian_motion). The transport length might be measured by transmission experiments of backscattering experiments [2] [3]
-
Mean free path simple scheme
External links
References
- ^ A. Ishimaru, Wave Propagation and Scattering in Random Media, Academic Press, New York, 1978.
- ^ Talanta, Volume 50, Issue 2, 13 September 1999, Pages 445-456
- ^ P. Snabre, A. Arhaliass, Anisotropic scattering of light in random media. Incoherent backscattered spot light,Appl. Optics 37 (18) (1998) 211 – 225.