Gravity assist: Difference between revisions
Wolfkeeper (talk | contribs) Undid revision 348938589 by 84.13.60.177 (talk) |
SEIBasaurus (talk | contribs) breaking for lunch will finalize later~~~~ |
||
| Line 1: | Line 1: | ||
In [[orbital mechanics]] and [[aerospace engineering]], a '''gravitational slingshot''', '''gravity assist''' or '''swing-by''' is the use of the relative movement and [[gravity]] of a [[planet]] or other celestial body to alter the path and speed of a [[spacecraft]], typically in order to save |
In [[orbital mechanics]] and [[aerospace engineering]], a '''gravitational slingshot''', '''gravity assist manuever''' or '''swing-by''' is the use of the relative movement and [[gravity]] of a [[planet]] or other celestial body to alter the path and speed of a [[spacecraft]], typically in order to save propellant, time, and expense. Gravity assistance can be used to accelerate, decelerate and/or re-direct the path of a spacecraft. The "assist" is provided by the motion (orbital angular momentum) of the gravitating bodyin as it pulls on the spacecraft.<ref>http://www2.jpl.nasa.gov/basics/bsf4-1.php Basics of Space Flight, Sec. 1 Ch. 4, NASA Jet Propulsion Laboratory</ref> |
||
== Explanation == |
== Explanation == |
||
| Line 5: | Line 5: | ||
[[Image:Grav slingshot simple 2.gif|thumb|200px|Over-simplified example of gravitational slingshot: the spacecraft's velocity changes by up to twice the planet's velocity]] |
[[Image:Grav slingshot simple 2.gif|thumb|200px|Over-simplified example of gravitational slingshot: the spacecraft's velocity changes by up to twice the planet's velocity]] |
||
A gravity assist or slingshot maneuver around a planet changes a spacecraft's [[velocity]] relative to the [[Sun]], even though it preserves the spacecraft's [[speed]] relative to the planet—as it must according to the law of [[conservation of energy]]. To a first approximation, from a large distance, the spacecraft appears to have bounced off the planet. Physicists call this an [[elastic collision]] even though no |
A gravity assist or slingshot maneuver around a planet changes a spacecraft's [[velocity]] relative to the [[Sun]], even though it preserves the spacecraft's [[speed]] relative to the planet—as it must according to the law of [[conservation of energy]]. To a first approximation, from a large distance, the spacecraft appears to have bounced off the planet. Physicists call this an [[elastic collision]] even though no actual contact occurs. |
||
Suppose that you are a "stationary" observer and that you see: a planet moving left at speed ''U''; a spaceship moving right at speed ''v''. If the spaceship is on the right path, it will pass close to the planet, moving at speed ''U + v'' relative to the planet's surface because the planet is moving in the opposite direction at speed ''U''. When the spaceship leaves orbit, it is still moving at ''U + v'' relative to the planet's surface but in the opposite direction, to the left; and since the planet is moving left at speed ''U'', the spaceship is moving left at speed ''2U + v'' from your point of view – its speed has increased by ''2U'', twice the speed at which the planet is moving. |
Suppose that you are a "stationary" observer and that you see: a planet moving left at speed ''U''; a spaceship moving right at speed ''v''. If the spaceship is on the right path, it will pass close to the planet, moving at speed ''U + v'' relative to the planet's surface because the planet is moving in the opposite direction at speed ''U''. When the spaceship leaves orbit, it is still moving at ''U + v'' relative to the planet's surface but in the opposite direction, to the left; and since the planet is moving left at speed ''U'', the spaceship is moving left at speed ''2U + v'' from your point of view – its speed has increased by ''2U'', twice the speed at which the planet is moving. |
||
| Line 11: | Line 11: | ||
It might seem that this is oversimplified since the details of the orbit have not been covered, but it turns out that if the spaceship travels in a path which forms a [[hyperbola]], it can leave the planet in the opposite direction without firing its engine, the speed gain at large distance is indeed ''2U'' once it has left the gravity of the planet far behind. |
It might seem that this is oversimplified since the details of the orbit have not been covered, but it turns out that if the spaceship travels in a path which forms a [[hyperbola]], it can leave the planet in the opposite direction without firing its engine, the speed gain at large distance is indeed ''2U'' once it has left the gravity of the planet far behind. |
||
This explanation might seem to violate the conservation of energy and momentum, but we have neglected the spacecraft's effects on the planet. The linear momentum gained by the spaceship is equal in magnitude to that lost by the planet, though the planet's |
This explanation might seem to violate the conservation of energy and momentum, but we have neglected the spacecraft's effects on the planet. The linear momentum gained by the spaceship is equal in magnitude to that lost by the planet, though the planet's enormous mass compared to the spacecraft makes the resulting change in its speed negligibly small. These effects on the planet are so slight (because planets are so much more massive than spacecraft) that they can be ignored in the calculation.<ref>[http://www.dur.ac.uk/bob.johnson/SL/ The Slingshot Effect], Durham University</ref> |
||
Realistic portrayals of encounters in space require the consideration of |
Realistic portrayals of encounters in space require the consideration of three dimensions. The same principles apply, only adding the planet's velocity to that of the spacecraft requires [[vector addition]], as shown below. |
||
[[Image:Grav slingshot diagram.png|center|400px|thumb|2 dimensional schematic of gravitational slingshot. The arrows show the direction in which the spacecraft is traveling before and after the encounter. The arrows' length shows the spacecraft's speed.]] |
[[Image:Grav slingshot diagram.png|center|400px|thumb|2 dimensional schematic of gravitational slingshot. The arrows show the direction in which the spacecraft is traveling before and after the encounter. The arrows' length shows the spacecraft's speed.]] |
||
| Line 19: | Line 19: | ||
Due to the [[reversibility of orbits]] gravitational slingshots can also be used to ''decelerate'' a spacecraft. [[Mariner 10]] did it in 1974 and [[MESSENGER]] is also doing it, both to reach [[Mercury (planet)|Mercury]]. |
Due to the [[reversibility of orbits]] gravitational slingshots can also be used to ''decelerate'' a spacecraft. [[Mariner 10]] did it in 1974 and [[MESSENGER]] is also doing it, both to reach [[Mercury (planet)|Mercury]]. |
||
If even more speed is needed, the most economical way |
If even more speed is needed than available from gravity assist alone, the most economical way to utilize a rocket burn is to do it near the [[periapsis]] (closest approach). A given rocket burn always provides the same change in velocity ([[delta-vee]]), but the change in kinetic energy is proportional to the vehicle's velocity at the time of the burn. So to get the most kinetic energy from the burn, the burn must occur at the vehicle's maximum velocity, at periapsis. [[#Powered_slingshots|Powered slingshots]] describes this technique in more detail. |
||
== Historical origins of the method == |
== Historical origins of the method == |
||
| Line 26: | Line 26: | ||
In his 1925 paper “Проблема полета при помощи реактивных аппаратов: межпланетные полеты” [Problems of flight by jet propulsion: interplanetary flights],<ref>Zander‘s 1925 paper, “Problems of flight by jet propulsion: interplanetary flights,” was translated by NASA. See NASA Technical Translation F-147 (1964); specifically, Section 7: Flight Around a Planet’s Satellite for Accelerating or Decelerating Spaceship, pages 290-292.</ref> [[Friedrich Zander]] made a similar argument. |
In his 1925 paper “Проблема полета при помощи реактивных аппаратов: межпланетные полеты” [Problems of flight by jet propulsion: interplanetary flights],<ref>Zander‘s 1925 paper, “Problems of flight by jet propulsion: interplanetary flights,” was translated by NASA. See NASA Technical Translation F-147 (1964); specifically, Section 7: Flight Around a Planet’s Satellite for Accelerating or Decelerating Spaceship, pages 290-292.</ref> [[Friedrich Zander]] made a similar argument. |
||
However, neither investigator realized that gravitational assists from planets ''along'' a spacecraft’s trajectory could propel a spacecraft and that therefore such assists could greatly reduce the amount of |
However, neither investigator realized that gravitational assists from planets ''along'' a spacecraft’s trajectory could propel a spacecraft and that therefore such assists could greatly reduce the amount of propellant required to travel among the planets.<ref>See page 13 of: Dowling, Richard L.; Kosmann, William J.; Minovitch, Michael A.; and Ridenoure, Rex W., “The origin of gravity-propelled interplanetary space travel” (IAA paper no. 90-630), presented at the 41st Congress of the International Astronautical Federation, which was held 6-12 October 1990 in Dresden, G.D.R. Available on-line at: http://www.gravityassist.com/IAF1/IAF1.pdf .</ref> That discovery was made by [[Michael Minovitch]] in 1961.<ref>Minovitch, Michael, "A method for determining interplanetary free-fall reconnaissance trajectories," Jet Propulsion Laboratory Technical Memo TM-312-130, pages 38-44 (23 August 1961).</ref> |
||
The gravity assist was first used in 1959 when the Soviet probe ''Luna 3'' photographed the far side of Earth's Moon. The maneuver relied on research performed at the [[Keldysh Institute of Applied Mathematics|Department of Applied Mathematics of Steklov Institute]].<ref>{{ru icon}} [http://www.applmat.ru/pages/anniver/achievment/3_appl_mech.htm 50th anniversary of Institute for Applied Mathematics - Applied celestial mechanics] - at the website of [[Keldysh Institute of Applied Mathematics]]</ref><ref>Egorov, Vsevolod Alexandrovich (1957) “Specific problems of a flight to the moon,” ''Physics - Uspekhi'', Vol. 63, No. 1a, pages 73-117. |
The gravity assist manuever was first used in 1959 when the Soviet probe ''Luna 3'' photographed the far side of Earth's Moon. The maneuver relied on research performed at the [[Keldysh Institute of Applied Mathematics|Department of Applied Mathematics of Steklov Institute]].<ref>{{ru icon}} [http://www.applmat.ru/pages/anniver/achievment/3_appl_mech.htm 50th anniversary of Institute for Applied Mathematics - Applied celestial mechanics] - at the website of [[Keldysh Institute of Applied Mathematics]]</ref><ref>Egorov, Vsevolod Alexandrovich (1957) “Specific problems of a flight to the moon,” ''Physics - Uspekhi'', Vol. 63, No. 1a, pages 73-117. |
||
Egorov’s work is mentioned in: Boris V. Rauschenbakh, Michael Yu. Ovchinnikov, and Susan M. P. McKenna-Lawlor, ''Essential Spaceflight Dynamics and Magnetospherics'' (Dordrecht, Netherlands: Kluwer Academic Publishers, 2002), pages 146-147. (The latter reference is available on-line at: http://books.google.com/books?id=m22bjIWZU9MC&pg=PA146&lpg=PA146&source=web&ots=U-tZaqVFhE&sig=LT_eEZcCegkd1dDS79glEkT28sw&hl=en#PPA146,M1 .)</ref> |
Egorov’s work is mentioned in: Boris V. Rauschenbakh, Michael Yu. Ovchinnikov, and Susan M. P. McKenna-Lawlor, ''Essential Spaceflight Dynamics and Magnetospherics'' (Dordrecht, Netherlands: Kluwer Academic Publishers, 2002), pages 146-147. (The latter reference is available on-line at: http://books.google.com/books?id=m22bjIWZU9MC&pg=PA146&lpg=PA146&source=web&ots=U-tZaqVFhE&sig=LT_eEZcCegkd1dDS79glEkT28sw&hl=en#PPA146,M1 .)</ref> |
||
| Line 42: | Line 42: | ||
Rocket engines can certainly be used to accelerate and decelerate the spacecraft. However, rocket thrust takes propellant, propellant has mass, and even a small amount of additional delta-v requirement translates to considerably larger amounts of propellant for raising the spacecraft from the Earth. This is because not only must the primary engines lift that propellant mass out of the Earth's gravity well, they must now lift the additional mass of the extra propellant used to lift that additional propellant. Thus the liftoff mass requirement [[rocket equation|increases exponentially]] with an increase in the required delta-v of the spacecraft. |
Rocket engines can certainly be used to accelerate and decelerate the spacecraft. However, rocket thrust takes propellant, propellant has mass, and even a small amount of additional delta-v requirement translates to considerably larger amounts of propellant for raising the spacecraft from the Earth. This is because not only must the primary engines lift that propellant mass out of the Earth's gravity well, they must now lift the additional mass of the extra propellant used to lift that additional propellant. Thus the liftoff mass requirement [[rocket equation|increases exponentially]] with an increase in the required delta-v of the spacecraft. |
||
With gravity |
With gravity assistance, a spacecraft can be accelerated or decelerated without the need for additional propellant. The combination of gravity assist and [[aerobraking]], where possible, can save signifant amountsof propellant. |
||
As an example, the [[MESSENGER]] mission |
As an example, the [[MESSENGER]] mission used gravity assist to slow the spacecraft on its way to Mercury, but aerobraking cannot be used for insertion into orbit about Mercury because Mercury has almost no atmosphere. |
||
Journeys to the nearest planets, [[Mars]] and [[Venus]], use a [[Hohmann transfer orbit]], an [[ellipse|elliptical]] path which starts as a [[tangent]] to one planet's orbit round the Sun and finishes as a tangent to the other. This method uses very nearly the smallest possible amount of fuel, but is very slow — it can take over a year to travel from Earth to Mars ([[Interplanetary_travel#Fuzzy_orbits|fuzzy orbits]] use even less fuel, but are even slower). |
Journeys to the nearest planets, [[Mars]] and [[Venus]], use a [[Hohmann transfer orbit]], an [[ellipse|elliptical]] path which starts as a [[tangent]] to one planet's orbit round the Sun and finishes as a tangent to the other. This method uses very nearly the smallest possible amount of fuel, but is very slow — it can take over a year to travel from Earth to Mars ([[Interplanetary_travel#Fuzzy_orbits|fuzzy orbits]] use even less fuel, but are even slower). |
||
Similarly it might take decades for a spaceship to travel to the outer planets ([[Jupiter]], [[Saturn]], [[Uranus]], etc.) using a Hohmann transfer orbit, and it would still require far too much |
Similarly it might take decades for a spaceship to travel to the outer planets ([[Jupiter]], [[Saturn]], [[Uranus]], etc.) using a Hohmann transfer orbit, and it would still require far too much propellant, because the spacecraft would have to travel for 500 million miles (800 million km) or more against the force of the Sun's gravity. Gravitational assist manuevers offer a way to gain speed without using any propellant, and all missions to the outer planets have used it.{{Fact|date=January 2008}} |
||
==Limits to slingshot use== |
==Limits to slingshot use== |
||
The main practical limit to the use of a |
The main practical limit to the use of a Gravity assist manuever is that planets and other large masses are not always in the right places to enable a voyage to a particular destination. For example the [[Voyager 1|Voyager]] missions which started in the late 1970s were made possible by the "[[Planetary Grand Tour|Grand Tour]]" alignment of Jupiter, Saturn, Uranus and Neptune. A similar alignment will not occur again until the middle of the 22nd century. That is an extreme case, but even for less ambitious missions there are years when the planets are scattered in unsuitable parts of their orbits. |
||
Another limit is caused by the atmosphere of the available planet. The closer the craft can |
Another limit is caused by the atmosphere of the available planet. The closer the craft can approach, the more boost it gets, because gravity falls off with the square of distance. If a craft gets too far into the atmosphere, however, the energy lost to friction can exceed that gained from the planet. On the other hand, this effect can be useful to accomplish [[aerobraking]]. There have also been (so far theoretical) proposals to use [[lift (force)|aerodynamic lift]] as the spacecraft flies through the atmosphere (an [[aerogravity assist]]). This could bend the trajectory through a larger angle than gravity alone, and hence increase the gain in energy. |
||
Interplanetary slingshots using the Sun itself are |
Interplanetary slingshots using the Sun itself are not possible because the Sun is at rest relative to the Solar System as a whole. However, thrusting when near the Sun has the same effect as the [[#Powered_slingshots|powered slingshot]] described above. This has the potential to magnify a spacecraft's thrusting power enormously, but is limited by the spacecraft's ability to resist the heat. |
||
An ''interstellar'' slingshot using the Sun is conceivable, involving for example an object coming from elsewhere in our galaxy and swinging past the Sun to boost its galactic travel. The energy and angular momentum would then come from the Sun's orbit around the [[Milky Way]]. The time scales involved for such an operation are considerably beyond current human capabilities, however. |
An ''interstellar'' slingshot using the Sun is conceivable, involving for example an object coming from elsewhere in our galaxy and swinging past the Sun to boost its galactic travel. The energy and angular momentum would then come from the Sun's orbit around the [[Milky Way]]. The time scales involved for such an operation are considerably beyond current human capabilities, however. |
||
| Line 71: | Line 71: | ||
===Galileo – a change of plan=== |
===Galileo – a change of plan=== |
||
The [[Galileo (spacecraft)|Galileo]] spacecraft was launched by [[NASA]] in 1989 aboard [[Space Shuttle Atlantis|Space Shuttle ''Atlantis'']]. Its original mission was designed to use a direct Hohmann transfer, but following the loss of the [[Space Shuttle Challenger|Space Shuttle ''Challenger'']], Galileo's intended [[Centaur (rocket stage)|Centaur]] booster rocket was no longer allowed to fly on Shuttles. Using a less-powerful solid booster rocket instead, Galileo flew by Venus once and Earth twice in order to reach Jupiter in December, 1995. |
The [[Galileo (spacecraft)|Galileo]] spacecraft was launched by [[NASA]] in 1989 aboard [[Space Shuttle Atlantis|Space Shuttle ''Atlantis'']]. Its original mission was designed to use a direct Hohmann transfer, but following the loss of the [[Space Shuttle Challenger|Space Shuttle ''Challenger'']], Galileo's intended [[Centaur (rocket stage)|Centaur]] booster rocket was no longer allowed to fly on Shuttles. Using a less-powerful solid booster rocket, the IUS, instead, Galileo flew by Venus once and Earth twice in order to reach Jupiter in December, 1995. |
||
The Galileo engineering inquest speculated (but was never able to conclusively prove) that this longer flight time coupled with the heat near Venus, is what caused lubricant in Galileo's main antenna to fail. This mechanical failure forced the use of a much less powerful backup antenna. |
The Galileo engineering inquest speculated (but was never able to conclusively prove) that this longer flight time coupled with the heat near Venus, is what caused lubricant in Galileo's main antenna to fail. This mechanical failure forced the use of a much less powerful backup antenna. |
||
| Line 77: | Line 77: | ||
Its subsequent tour of the [[Moons of Jupiter|Jovian moons]] also used numerous slingshot maneuvers with those moons to conserve fuel and maximize the number of encounters. |
Its subsequent tour of the [[Moons of Jupiter|Jovian moons]] also used numerous slingshot maneuvers with those moons to conserve fuel and maximize the number of encounters. |
||
===The Ulysses probe changed the |
===The Ulysses probe changed the plane of its trajectory=== |
||
In 1990, the [[European Space Agency|ESA]] launched the spacecraft [[Ulysses (spacecraft)|Ulysses]] to study the [[geographical pole|polar]] regions of the [[Sun]]. All the planets orbit approximately in a plane aligned with the equator of the Sun. To move to an orbit passing over the poles of the Sun, the spacecraft would have to eliminate the 30 km/s speed it inherited from the Earth's orbit around the Sun and gain the speed needed to orbit the Sun in the pole-to-pole plane — tasks which were impossible with current [[spacecraft propulsion]] systems. |
In 1990, the [[European Space Agency|ESA]] launched the spacecraft [[Ulysses (spacecraft)|Ulysses]] to study the [[geographical pole|polar]] regions of the [[Sun]]. All the planets orbit approximately in a plane aligned with the equator of the Sun. To move to an orbit passing over the poles of the Sun, the spacecraft would have to eliminate the 30 km/s speed it inherited from the Earth's orbit around the Sun and gain the speed needed to orbit the Sun in the pole-to-pole plane — tasks which were impossible with current [[spacecraft propulsion]] systems. |
||
| Line 100: | Line 100: | ||
A well-established way to get more energy from a gravity assist is to fire a rocket engine at [[periapsis]] where a spacecraft is at its maximum velocity. |
A well-established way to get more energy from a gravity assist is to fire a rocket engine at [[periapsis]] where a spacecraft is at its maximum velocity. |
||
Rocket engines produce the same |
Rocket engines produce the same acelleration regardless of their initial velocity. A rocket acting on a fixed object, as in a static firing, does no useful work at all; the rocket's stored energy is entirely expended on its propellant. But when the rocket and payload move, the force applied to the payload by the rocket during any time interval acts through the distance the rocket and payload move during that time. Force acting through a distance is the definition of [[mechanical work|mechanical energy or work]]. So the farther the rocket and payload move during any given interval, i.e., the faster they move, the greater the kinetic energy imparted to the payload by the rocket. (This is why rockets are seldom used on slow-moving vehicles; they're simply too inefficient when used in that manner.) |
||
Energy is still conserved, however. The additional energy imparted to the payload is exactly matched by a decrease in energy imparted to the propellant being expelled behind the rocket because the speed of the rocket subtracts from the propellant exhaust velocity. But we don't care about the propellant, so the faster we can move during a rocket burn, the better. |
Energy is still conserved, however. The additional energy imparted to the payload is exactly matched by a decrease in energy imparted to the propellant being expelled behind the rocket because the speed of the rocket subtracts from the propellant exhaust velocity. But we don't care about the propellant, so the faster we can move during a rocket burn, the better. |
||
Revision as of 16:07, 25 March 2010
In orbital mechanics and aerospace engineering, a gravitational slingshot, gravity assist manuever or swing-by is the use of the relative movement and gravity of a planet or other celestial body to alter the path and speed of a spacecraft, typically in order to save propellant, time, and expense. Gravity assistance can be used to accelerate, decelerate and/or re-direct the path of a spacecraft. The "assist" is provided by the motion (orbital angular momentum) of the gravitating bodyin as it pulls on the spacecraft.[1]
Explanation
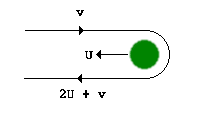
A gravity assist or slingshot maneuver around a planet changes a spacecraft's velocity relative to the Sun, even though it preserves the spacecraft's speed relative to the planet—as it must according to the law of conservation of energy. To a first approximation, from a large distance, the spacecraft appears to have bounced off the planet. Physicists call this an elastic collision even though no actual contact occurs.
Suppose that you are a "stationary" observer and that you see: a planet moving left at speed U; a spaceship moving right at speed v. If the spaceship is on the right path, it will pass close to the planet, moving at speed U + v relative to the planet's surface because the planet is moving in the opposite direction at speed U. When the spaceship leaves orbit, it is still moving at U + v relative to the planet's surface but in the opposite direction, to the left; and since the planet is moving left at speed U, the spaceship is moving left at speed 2U + v from your point of view – its speed has increased by 2U, twice the speed at which the planet is moving.
It might seem that this is oversimplified since the details of the orbit have not been covered, but it turns out that if the spaceship travels in a path which forms a hyperbola, it can leave the planet in the opposite direction without firing its engine, the speed gain at large distance is indeed 2U once it has left the gravity of the planet far behind.
This explanation might seem to violate the conservation of energy and momentum, but we have neglected the spacecraft's effects on the planet. The linear momentum gained by the spaceship is equal in magnitude to that lost by the planet, though the planet's enormous mass compared to the spacecraft makes the resulting change in its speed negligibly small. These effects on the planet are so slight (because planets are so much more massive than spacecraft) that they can be ignored in the calculation.[2]
Realistic portrayals of encounters in space require the consideration of three dimensions. The same principles apply, only adding the planet's velocity to that of the spacecraft requires vector addition, as shown below.

Due to the reversibility of orbits gravitational slingshots can also be used to decelerate a spacecraft. Mariner 10 did it in 1974 and MESSENGER is also doing it, both to reach Mercury.
If even more speed is needed than available from gravity assist alone, the most economical way to utilize a rocket burn is to do it near the periapsis (closest approach). A given rocket burn always provides the same change in velocity (delta-vee), but the change in kinetic energy is proportional to the vehicle's velocity at the time of the burn. So to get the most kinetic energy from the burn, the burn must occur at the vehicle's maximum velocity, at periapsis. Powered slingshots describes this technique in more detail.
Historical origins of the method
In his paper “Тем кто будет читать, чтобы строить” (To whoever will read [this paper] in order to build [an interplanetary rocket]),[3] which he dated “1918-1919,”[4] Yuri Kondratyuk suggested that a spacecraft traveling between two planets could be accelerated at the beginning of its trajectory and decelerated at the end of its trajectory by using the gravity of the two planets' moons.
In his 1925 paper “Проблема полета при помощи реактивных аппаратов: межпланетные полеты” [Problems of flight by jet propulsion: interplanetary flights],[5] Friedrich Zander made a similar argument.
However, neither investigator realized that gravitational assists from planets along a spacecraft’s trajectory could propel a spacecraft and that therefore such assists could greatly reduce the amount of propellant required to travel among the planets.[6] That discovery was made by Michael Minovitch in 1961.[7]
The gravity assist manuever was first used in 1959 when the Soviet probe Luna 3 photographed the far side of Earth's Moon. The maneuver relied on research performed at the Department of Applied Mathematics of Steklov Institute.[8][9]
Why gravitational slingshots are used
A spacecraft traveling to an inner planet will accelerate because it is falling toward the Sun, and a spacecraft traveling to an outer planet will decelerate because it is leaving the vicinity of the Sun.
Although it is true that the orbital speed of an inner planet is greater than that of the Earth, a spacecraft traveling to an inner planet is accelerated by the Sun's gravity to a speed notably greater than the orbital speed of that destination planet. If the spacecraft's purpose is only to fly by the inner planet, then there is typically no need to slow the spacecraft. However, if the spacecraft is to be inserted into orbit about that inner planet, then there must be a mechanism to slow the spacecraft.
Likewise, although it is true that the orbital speed of an outer planet is less than that of the Earth, a spacecraft traveling to an outer planet is decelerated by the Sun's gravity to a speed far less than the orbital speed of that outer planet. Thus there must be a mechanism to accelerate the spacecraft. Also, accelerating the spacecraft will, of course, reduce the travel time.
Rocket engines can certainly be used to accelerate and decelerate the spacecraft. However, rocket thrust takes propellant, propellant has mass, and even a small amount of additional delta-v requirement translates to considerably larger amounts of propellant for raising the spacecraft from the Earth. This is because not only must the primary engines lift that propellant mass out of the Earth's gravity well, they must now lift the additional mass of the extra propellant used to lift that additional propellant. Thus the liftoff mass requirement increases exponentially with an increase in the required delta-v of the spacecraft.
With gravity assistance, a spacecraft can be accelerated or decelerated without the need for additional propellant. The combination of gravity assist and aerobraking, where possible, can save signifant amountsof propellant.
As an example, the MESSENGER mission used gravity assist to slow the spacecraft on its way to Mercury, but aerobraking cannot be used for insertion into orbit about Mercury because Mercury has almost no atmosphere.
Journeys to the nearest planets, Mars and Venus, use a Hohmann transfer orbit, an elliptical path which starts as a tangent to one planet's orbit round the Sun and finishes as a tangent to the other. This method uses very nearly the smallest possible amount of fuel, but is very slow — it can take over a year to travel from Earth to Mars (fuzzy orbits use even less fuel, but are even slower).
Similarly it might take decades for a spaceship to travel to the outer planets (Jupiter, Saturn, Uranus, etc.) using a Hohmann transfer orbit, and it would still require far too much propellant, because the spacecraft would have to travel for 500 million miles (800 million km) or more against the force of the Sun's gravity. Gravitational assist manuevers offer a way to gain speed without using any propellant, and all missions to the outer planets have used it.[citation needed]
Limits to slingshot use
The main practical limit to the use of a Gravity assist manuever is that planets and other large masses are not always in the right places to enable a voyage to a particular destination. For example the Voyager missions which started in the late 1970s were made possible by the "Grand Tour" alignment of Jupiter, Saturn, Uranus and Neptune. A similar alignment will not occur again until the middle of the 22nd century. That is an extreme case, but even for less ambitious missions there are years when the planets are scattered in unsuitable parts of their orbits.
Another limit is caused by the atmosphere of the available planet. The closer the craft can approach, the more boost it gets, because gravity falls off with the square of distance. If a craft gets too far into the atmosphere, however, the energy lost to friction can exceed that gained from the planet. On the other hand, this effect can be useful to accomplish aerobraking. There have also been (so far theoretical) proposals to use aerodynamic lift as the spacecraft flies through the atmosphere (an aerogravity assist). This could bend the trajectory through a larger angle than gravity alone, and hence increase the gain in energy.
Interplanetary slingshots using the Sun itself are not possible because the Sun is at rest relative to the Solar System as a whole. However, thrusting when near the Sun has the same effect as the powered slingshot described above. This has the potential to magnify a spacecraft's thrusting power enormously, but is limited by the spacecraft's ability to resist the heat.
An interstellar slingshot using the Sun is conceivable, involving for example an object coming from elsewhere in our galaxy and swinging past the Sun to boost its galactic travel. The energy and angular momentum would then come from the Sun's orbit around the Milky Way. The time scales involved for such an operation are considerably beyond current human capabilities, however.
Another theoretical limit is based on general relativity. If a spacecraft gets close to the Schwarzschild radius of a black hole (the ultimate gravity well), space becomes so curved that slingshot orbits require more energy to escape than the energy that could be added by the black hole's motion.
A rotating black hole might provide additional assistance, if its spin axis points the right way. General relativity predicts that a large spinning mass produces frame-dragging — close to the object, space itself is dragged around in the direction of the spin. In theory an ordinary star produces this effect, although attempts to measure it around the Sun have produced no clear results. Experiments performed by Gravity Probe B looking for frame-dragging effects caused by the Earth have also not revealed conclusive results. General relativity predicts that a spinning black hole is surrounded by a region of space, called the ergosphere, within which standing still (with respect to the black hole's spin) is impossible, because space itself is dragged at the speed of light in the same direction as the black hole's spin. The Penrose process may offer a way to gain energy from the ergosphere, although it would require the spaceship to dump some "ballast" into the black hole, and the spaceship would have had to expend energy to carry the "ballast" to the black hole.
Timeline of notable examples
Mariner 10 – first use
The Mariner 10 probe was the first spacecraft to use the gravitational slingshot effect to reach another planet, passing by Venus on February 5, 1974, on its way to becoming the first spacecraft to explore Mercury.
Voyager 1 – furthest human-made object
As of January 21, 2010, Voyager 1 is over 16.81 terameters (1.681×1013 meters, or 1.681×1010 km, 112.4 AU, or 10.4 billion miles) from the Sun, and is in the boundary zone between the Solar System and interstellar space. It gained the energy to escape the Sun's gravity completely by performing slingshot maneuvers around Jupiter and Saturn.[10][11]
Galileo – a change of plan
The Galileo spacecraft was launched by NASA in 1989 aboard Space Shuttle Atlantis. Its original mission was designed to use a direct Hohmann transfer, but following the loss of the Space Shuttle Challenger, Galileo's intended Centaur booster rocket was no longer allowed to fly on Shuttles. Using a less-powerful solid booster rocket, the IUS, instead, Galileo flew by Venus once and Earth twice in order to reach Jupiter in December, 1995.
The Galileo engineering inquest speculated (but was never able to conclusively prove) that this longer flight time coupled with the heat near Venus, is what caused lubricant in Galileo's main antenna to fail. This mechanical failure forced the use of a much less powerful backup antenna.
Its subsequent tour of the Jovian moons also used numerous slingshot maneuvers with those moons to conserve fuel and maximize the number of encounters.
The Ulysses probe changed the plane of its trajectory
In 1990, the ESA launched the spacecraft Ulysses to study the polar regions of the Sun. All the planets orbit approximately in a plane aligned with the equator of the Sun. To move to an orbit passing over the poles of the Sun, the spacecraft would have to eliminate the 30 km/s speed it inherited from the Earth's orbit around the Sun and gain the speed needed to orbit the Sun in the pole-to-pole plane — tasks which were impossible with current spacecraft propulsion systems.
The craft was sent towards Jupiter, aimed to arrive at a point in space just "in front of" and "below" the planet. As it passed Jupiter, the probe 'fell' through the planet's gravity field, borrowing a minute amount of momentum from the planet; after it had passed Jupiter, the velocity change had bent the probe's trajectory up out of the plane of the planetary orbits, placing it in an orbit that passed over the poles of the Sun. This maneuver required only enough fuel to send Ulysses to a point near Jupiter, which is well within current technologies.
MESSENGER
The MESSENGER mission is making extensive use of gravity assists to slow its speed before orbiting Mercury. The MESSENGER mission includes one flyby of Earth, two flybys of Venus, and three flybys of Mercury before finally arriving at Mercury in March 2011 with a velocity low enough to permit orbit insertion with the available fuel. Although the flybys are primarily orbital maneuvers, each provides an opportunity for significant scientific observations.
The Cassini probe – multiple gravity assists
The Cassini probe passed by Venus twice, then Earth, and finally Jupiter on the way to Saturn. The 6.7-year transit was slightly longer than the six years needed for a Hohmann transfer, but cut the total amount of delta V needed to about 2 km/s, so that the large and heavy Cassini probe was able to reach Saturn even with the small boosters available. A Hohmann transfer to Saturn would require a total of 15.7 km/s delta V (disregarding Earth's and Saturn's own gravity wells, and disregarding aerobraking), which is not within the capabilities of current spacecraft boosters.


Solar Probe +
The NASA Solar Probe+ mission, scheduled for launch in 2015, uses multiple gravity assists at Venus to remove the Earth's angular momentum from the orbit, in order to drop down to a distance of 9.5 solar radii from the sun. This will be the closest approach to the sun of any space mission.
Powered slingshots
A well-established way to get more energy from a gravity assist is to fire a rocket engine at periapsis where a spacecraft is at its maximum velocity.
Rocket engines produce the same acelleration regardless of their initial velocity. A rocket acting on a fixed object, as in a static firing, does no useful work at all; the rocket's stored energy is entirely expended on its propellant. But when the rocket and payload move, the force applied to the payload by the rocket during any time interval acts through the distance the rocket and payload move during that time. Force acting through a distance is the definition of mechanical energy or work. So the farther the rocket and payload move during any given interval, i.e., the faster they move, the greater the kinetic energy imparted to the payload by the rocket. (This is why rockets are seldom used on slow-moving vehicles; they're simply too inefficient when used in that manner.)
Energy is still conserved, however. The additional energy imparted to the payload is exactly matched by a decrease in energy imparted to the propellant being expelled behind the rocket because the speed of the rocket subtracts from the propellant exhaust velocity. But we don't care about the propellant, so the faster we can move during a rocket burn, the better.
So if we want to impart the maximum amount of kinetic energy to a spacecraft whose velocity varies with time, we should do it when it's moving the fastest. During a gravity assist, this happens at periapsis, the closest approach to the planet, so that's when we do the burn.
Another way to look at it is that by bringing in propellant as we fall into the planet's gravity well and leaving it behind there, we are able to extract much of the gravitational potential energy that was contained in that propellant.
There are also proposals to use aerodynamic lift at the point of closest approach (an aerogravity assist), to achieve a larger deflection and hence more energy gain.
See also
- 3753 Cruithne: an asteroid which periodically has gravitational slingshot encounters with Earth.
- Delta-v budget
- Dynamical friction
- Flyby anomaly: an anomalous delta-v increase during gravity assists
- Interplanetary Transport Network
- Gravitational keyhole
- Michael Minovitch
- N-body problem
- New Horizons: a gravity-assisted mission (flying past Jupiter) to reach Pluto in 2015.
- The Oberth effect: doing burns deep in gravity fields to gain speed
- Pioneer 10
- Pioneer 11
- Pioneer H
- Ulysses
- Voyager 1
- Voyager 2
- MESSENGER
- STEREO: a gravity-assisted mission which used Earth's Moon to eject two spacecraft from Earth's orbit into heliocentric orbit
References
- ^ http://www2.jpl.nasa.gov/basics/bsf4-1.php Basics of Space Flight, Sec. 1 Ch. 4, NASA Jet Propulsion Laboratory
- ^ The Slingshot Effect, Durham University
- ^ Kondratyuk’s paper is included in the book: Mel’kumov, T. M., ed., Pionery Raketnoy Tekhniki [Pioneers of Rocketry: Selected Papers] (Moscow, U.S.S.R.: Institute for the History of Natural Science and Technology, Academy of Sciences of the USSR, 1964). An English translation of Kondratyuk’s paper was made by NASA. See: NASA Technical Translation F-9285, pages 15-56 (Nov. 1, 1965).
- ^ In 1938, when Kondratyuk submitted his manuscript “To whoever will read in order to build” for publication, he dated the manuscript “1918-1919,” although it was apparent that the manuscript had been revised at various times. See page 49 of NASA Technical Translation F-9285 (Nov. 1, 1965).
- ^ Zander‘s 1925 paper, “Problems of flight by jet propulsion: interplanetary flights,” was translated by NASA. See NASA Technical Translation F-147 (1964); specifically, Section 7: Flight Around a Planet’s Satellite for Accelerating or Decelerating Spaceship, pages 290-292.
- ^ See page 13 of: Dowling, Richard L.; Kosmann, William J.; Minovitch, Michael A.; and Ridenoure, Rex W., “The origin of gravity-propelled interplanetary space travel” (IAA paper no. 90-630), presented at the 41st Congress of the International Astronautical Federation, which was held 6-12 October 1990 in Dresden, G.D.R. Available on-line at: http://www.gravityassist.com/IAF1/IAF1.pdf .
- ^ Minovitch, Michael, "A method for determining interplanetary free-fall reconnaissance trajectories," Jet Propulsion Laboratory Technical Memo TM-312-130, pages 38-44 (23 August 1961).
- ^ Template:Ru icon 50th anniversary of Institute for Applied Mathematics - Applied celestial mechanics - at the website of Keldysh Institute of Applied Mathematics
- ^ Egorov, Vsevolod Alexandrovich (1957) “Specific problems of a flight to the moon,” Physics - Uspekhi, Vol. 63, No. 1a, pages 73-117. Egorov’s work is mentioned in: Boris V. Rauschenbakh, Michael Yu. Ovchinnikov, and Susan M. P. McKenna-Lawlor, Essential Spaceflight Dynamics and Magnetospherics (Dordrecht, Netherlands: Kluwer Academic Publishers, 2002), pages 146-147. (The latter reference is available on-line at: http://books.google.com/books?id=m22bjIWZU9MC&pg=PA146&lpg=PA146&source=web&ots=U-tZaqVFhE&sig=LT_eEZcCegkd1dDS79glEkT28sw&hl=en#PPA146,M1 .)
- ^ Cassini-Huygens: Operations - Gravity Assists
- ^ http://www.heavens-above.com/solar-escape.asp?lat=0&lng=0&loc=Unspecified&alt=0&tz=CET
External links
- Slingshot effect
- Animation of Cassini Huygens gravitational sling shot
- MathPages - Gravitational Slingshot Theory
- A Quick Gravity Assist Primer
- An artistical simulation of an unstable planetary system showing gravitational slingshots and other phenomena
- Tools to calculate effects of a swing-by, such as the Swing-by Calculator
