Monoid (category theory): Difference between revisions
Appearance
Content deleted Content added
No edit summary |
m Bot: links syntax |
||
| Line 1: | Line 1: | ||
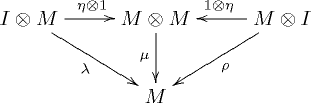
In [[category theory]], a '''monoid''' (or '''monoid object''') <math>(M,\mu,\eta)</math> in a [[monoidal category]] '''C''' is an object ''M'' together with two [[morphism |
In [[category theory]], a '''monoid''' (or '''monoid object''') <math>(M,\mu,\eta)</math> in a [[monoidal category]] '''C''' is an object ''M'' together with two [[morphism]]s |
||
* <math>\mu : M\otimes M\to M</math> called ''multiplication'', |
* <math>\mu : M\otimes M\to M</math> called ''multiplication'', |
||
* and <math>\eta : I\to M</math> called ''unit'', |
* and <math>\eta : I\to M</math> called ''unit'', |
||
Revision as of 05:04, 22 October 2010
In category theory, a monoid (or monoid object) in a monoidal category C is an object M together with two morphisms
- called multiplication,
- and called unit,
such that the diagrams
commute. In the above notations, I is the unit element and , and are respectively the associativity, the left identity and the right identity of the monoidal category C.
Dually, a comonoid in a monoidal category C is a monoid in the dual category .
Suppose that the monoidal category C has a symmetry . A monoid in C is symmetric when
- .
Examples
- A monoid object in Set (with the monoidal structure induced by the cartesian product) is a monoid in the usual sense.
- A monoid object in Top (with the monoidal structure induced by the product topology) is a topological monoid.
- A monoid object in the category of monoids (with the direct product of monoids) is just a commutative monoid. This follows easily from the Eckmann–Hilton theorem.
- A monoid object in the category of complete join-semilattices Sup (with the monoidal structure induced by the cartesian product) is a unital quantale.
- A monoid object in (Ab, ⊗Z, Z) is a ring.
- For a commutative ring R, a monoid object in (R-Mod, ⊗R, R) is an R-algebra.
- A monoid object in K-Vect (again, with the tensor product) is a K-algebra, a comonoid object is a K-coalgebra.
- For any category C, the category [C,C] of its endofunctors has a monoidal structure induced by the composition. A monoid object in [C,C] is a monad on C.
Categories of monoids
Given two monoids and in a monoidal category C, a morphism is a morphism of monoids when
- ,
- .
The category of monoids in C and their monoid morphisms is written .
See also
References
- Mati Kilp, Ulrich Knauer, Alexander V. Mikhalov, Monoids, Acts and Categories (2000), Walter de Gruyter, Berlin ISBN 3-11-015248-7