Wikipedia:Reference desk/Mathematics

Welcome to the mathematics section
of the Wikipedia reference desk.

skip to bottom

Select a section:

• Computing
• Entertainment
• Humanities
• Language
• Mathematics
• Science
• Miscellaneous
• Archives

Want a faster answer?

Main page: Help searching Wikipedia

   

How can I get my question answered?

• Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
• Post your question to only one section, providing a short header that gives the topic of your question.
• Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
• Don't post personal contact information – it will be removed. Any answers will be provided here.
• Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
• Note:
  • We don't answer (and may remove) questions that require medical diagnosis or legal advice.
  • We don't answer requests for opinions, predictions or debate.
  • We don't do your homework for you, though we'll help you past the stuck point.
  • We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.

Ready? Ask a new question!

How do I answer a question?

Main page: Wikipedia:Reference desk/Guidelines

• The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.

See also:

• Teahouse
• Help desk
• Village pump
• Help manual

October 30

Divisor of a Mersenne prime

Resolved

Given a Mersenne prime $M_{q}=2^{q}-1$, empirically I've tested $q|M_{q}-1$ for all 47 known Mersenne primes. Is this a general property? The converse isn't true--that is, if $n|M_{n}-1$, $M_{n}$ isn't necessarily a Mersenne prime. The first counterexample is $2^{341}-2$, which is divisible by 11 and 31, so by 11*31 = 341. I haven't been able to make much progress and it seems like this would have been studied before. 67.158.43.41 (talk) 05:13, 30 October 2010 (UTC)

$M_{q}-1=2^{q}-2=2(2^{q-1}-1)$. Therefore, if q is odd, then $q|M_{q}-1$ if $q|2^{q-1}-1$. But Fermat's little theorem says that if q is an odd prime then $q|2^{q-1}-1$. This explains why $q|M_{q}-1$ for all Mersenne primes (note that q must be prime if M_q is a Mersenne prime). However, as you observe, the converse if not true - there are composite numbers called pseudoprimes to base 2 (also known as a Poulet numbers) which also satisfy $q|2^{q-1}-1$, and hence $q|2^{q}-2$. The smallest Poulet numbers are 341, 561 and 645. Gandalf61 (talk) 09:28, 30 October 2010 (UTC)

Ah of course, how simple. Thanks for the name for Poulet numbers! 67.158.43.41 (talk) 11:18, 30 October 2010 (UTC)

The mathematical spontaneity of coffee stirrers

Is this http://i56.tinypic.com/2urqjpj.png the only arrangement of four straight lines that allows each line to cross all the other lines without any triple or quadruple crossing points? And if it is, how can I prove it? —Preceding unsigned comment added by 89.243.205.241 (talk) 20:51, 30 October 2010 (UTC)

I don't know but here's a math joke: Why do we stir coffee? Answer: To make it sweet! All right, wise guy, then why do we put in sugar first? So that when it dissolves we know we can stop stirring! 84.153.183.246 (talk) 21:00, 30 October 2010 (UTC)

To prove anything about this I think you need to make the question a bit more precise. What makes two arrangements the same? I think I understand what you're asking and I'm pretty sure the answer is "yes", but I'm not so sure about how to state it in a precise way. Maybe someone else can help with that. Rckrone (talk) 22:43, 30 October 2010 (UTC)

I do not have much maths education, but I'll try. First off I'll say the colours in the picture don't mean anything. Secondly, an arrangement would be the same as another one if it was a rotation, a reflection (although obviously in this case my current arrangement has reflectional symmetry) or if it just had the crossover points shifted along the lines without the order of crossover points on any of the lines actually changing. 89.243.205.241 (talk) 23:02, 30 October 2010 (UTC)

Here's a sketch of an argument: the first 3 stirrers form a triangle. The fourth stirrer (call it A) can cross each of first 3 either within the segment that forms a side of the triangle, or outside of it. If stirrer A crosses into the triangle, it has to later cross back out. So then it must cross the triangle an even number of times (which means 0 or twice). If it crosses the triangle zero times, then choose the first and last stirrer it crosses and call these B and C, with the remaining one being D. Stirrers A,B,C form their own triangle, and stirrer D crosses stirrer A between A's intersection with B and C, so D crosses the triangle formed by A,B,C and therefore must cross it twice. So the only possible arrangement is for one of the stirrers to cross the triangle formed by the other 3 exactly twice, and the remaining crossing is outside the triangle. You would then need to verify that all the ways for that to happen look essentially the same. Rckrone (talk) 23:59, 30 October 2010 (UTC)

For showing all combinations are "essentially the same" it could be much prettier to take one line as the x axis and the other line as the y axis. Formally, this can be justified by use of a linear transformation. The quadrilateral also seems to form in the quadrant containing the intersection of the remaining two lines (where I'm assuming no line is parallel or equal to any other). A proof by cases on the number of intersections with each ray +x, -x, +y, and -y seems relatively brief. Mirror and rotational symmetry cut the number of cases down very far.

Somewhat informally, I think you're trying to show than any 4 nondegenerate (non-parallel and unequal; no triple or quadruple intersections) lines enclose exactly 1 trapezoid and 2 triangles, all other regions being unbounded. The trapezoid shares exactly 1 side with each triangle, the triangles share no sides, and all three shapes share exactly one vertex.

A higher level but more difficult argument would be to show that the four lines x=0, y=0, y=1-x, and y=3-2x can be continuously deformed into any nondegenerate arrangement of 4 lines, where the topology given by the regions formed and their adjacencies is unaltered by any continuous deformation, i.e. is a topological property. I've studied very little topology, but I'd suspect many of the tools for this proof are well-known to those who have studied it more. 67.158.43.41 (talk) 11:40, 31 October 2010 (UTC)

Algorithm for next term in series

A while back, my teacher showed the class a way to construct a polynomial function that could satisfy any series (example, for a series like -2, 4, 8, -2.3, and 0, this algorithm would produce a function f(n) such that f(1) = -2, f(2) = 4, etc). I forget how it worked though, although I remember it has something to do with subtracting each term by the one next to it, and continuing this until they're all zero. 76.68.247.201 (talk) 22:06, 30 October 2010 (UTC)

That's one way of doing it. Another is given in Lagrange polynomial. Algebraist 22:22, 30 October 2010 (UTC)

What you're remembering is maybe Newton's forward difference formula. You can also do it by solving a system of linear equations; see [1], for example. —Bkell (talk) 23:52, 30 October 2010 (UTC)

Thanks! 76.68.247.201 (talk) 03:46, 31 October 2010 (UTC)

The J formula is etc=.({.[:{."1(2-/\])^:([:i.#))^:2 and the test run 20 etc _2 4 8 _2.3 0 produces _2 4 8 _2.3 0 81 346 939.5 2045.2 3886 6724 10860.5 16636 24430.2 34662 47789.5 64310 84760 109715.2 139790.5 Bo Jacoby (talk) 07:29, 31 October 2010 (UTC).

Would you mind verbally explaining that syntactic magic? Just curious. (I know I could look it up, but it seems way more efficient for someone knowledgeable to just say what it means.) 67.158.43.41 (talk) 11:41, 31 October 2010 (UTC)

Sure! Here are some commented intermediate results.

  n=._2 4 8 _2.3 0 NB. input
  D=.2-/\] NB. computing Differences (-) between pairs (2)
  D n NB. once
_6 _4 10.3 _2.3
  D D n NB. twice
_2 _14.3 12.6
  D^:3 n NB. three times
12.3 _26.9
  D^:0 1 2 3 4 n NB. table of differences
  _2     4    8 _2.3 0
  _6    _4 10.3 _2.3 0
  _2 _14.3 12.6    0 0
12.3 _26.9    0    0 0
39.2     0    0    0 0
  T=.[:{."1 D^:([:i.#)NB. first ({.) column ("1) is the Transform 
  T n NB. Transform of input
_2 _6 _2 12.3 39.2
  10 {. T n NB. extend the Transform with zeroes
_2 _6 _2 12.3 39.2 0 0 0 0 0
  T 10 {. T n NB. Retransform to obtain the extended input
_2 4 8 _2.3 0 81 346 939.5 2045.2 3886
  etc =.({. T)^:2 NB. define the function
  10 etc n NB. see it work
_2 4 8 _2.3 0 81 346 939.5 2045.2 3886
  etc f. NB. express the function without using intermediate functions T and D.
({. ([: {."1 (2 -/\ ])^:([: i. #)))^:2

You may download from www.jsoftware.com and play with it yourself. Have fun! Bo Jacoby (talk) 08:06, 1 November 2010 (UTC).

Thank you! I enjoy functional programming conceptually, and this extreme version of it is quite interesting. I had trouble figuring out precisely what the transform was doing, and the rules of currying and uncurrying are unclear to me. But still, I had fun going through the first half or so of the tutorial; maybe I'll finish it someday :). 67.158.43.41 (talk) 22:21, 5 November 2010 (UTC)

October 31

Pumping Lemma

Hi, I've been trying to understand the pumping lemma to no avail. I understand that it has something to do with the pigeon hole principle and that the idea is to get a repeating string x(y^i)z. I just still don't understand how to pick the pumping string, or figure out the minimum pumping length, or how to solve a proof. The wikipedia page made some sense but it was confusing too :/ —Preceding unsigned comment added by Legolas52 (talk • contribs) 00:09, 31 October 2010 (UTC)

I'm guessing you mean the pumping lemma for regular languages. I'm not sure what you mean by "how to pick the pumping string". Finding a pumping length isn't hard, though. For a regular language, write out its finite state automaton. Count the number of states--that's a pumping length. I say "a" pumping length because any larger length than the number of states actually works as well, and it may well be the case that a smaller number could work. The point is, the number of states *does* work. The proof of the pumping lemma is actually pretty simple. For a regular language where you've found its finite state automaton and the number of states in that automaton , say p, try an input string of p+1 characters. As the automaton processes these characters, the current state jumps around. How many possible different states can be visited during processing? At most, each character can cause a jump to a new, unvisited state, giving p+1 states visited--but there are only p states in the automaton. So, not every jump can be to a new, unvisited state, forcing some state to have been visited twice. That double visit is the key--the first visit is just before the first character of the "y" string and the last visit is just after the last character of the "y" string has been processed. We could simply skip "y", or we could repeat "y" as many times as we feel like, which simply corresponds to going around in the loop "y" traverses.

How to "solve a proof" is a bit vague, but I think you mean to ask how one uses the pumping lemma to show that a given language is not regular. (The pumping lemma doesn't show a language is regular; it can only be used to prove that no finite state automaton can accept a particular language, for if one existed, the pumping lemma would apply.) These lecture notes are decent and provide a number of examples starting at "Applications". To choose a good counterexample string (which might have been what you meant by "pumping string") sometimes just takes insight into the problem, though other times the first string you would ever think of trying to pump is the right one. There's no real general method. I remember spending a few hours on one pumping lemma problem once and finally finding a complicated but correct counterexample. (The prof. hadn't intended the question to be so hard and replaced it after I had completed it. The replacement, as I recall, was almost trivial in that the first thing worked obviously.) 67.158.43.41 (talk) 11:10, 31 October 2010 (UTC)

Analytic injective functions on the extended complex plane

Hello RD. I am aware that any analytic injective function on the whole complex plane (i.e. entire, injective), must be of the form az+b, a!=0 - I just found a very nice proof using the Casorate-Weierstrass theorem, much more concise than my previous efforts. However, what happens in the case of the extended complex plane? I'd be astonished if the situation remained the same, only functions of the form az+b, but I can't think for the life of me how to investigate the thing.

Would it be easier to operate on the Riemann sphere, perhaps? I've just recently been introduced to the concept of a Riemann surface, atlases etc., so I'd probably be happy with any theory you would consider 'simpler' than that - thankyou for suggestions. Estrenostre (talk) 01:27, 31 October 2010 (UTC)

Actually, the situation is very similar. Suppose your injective function f maps the point at infinity to d. Consider g(z) = (dz + 1)/(z - d). g maps d to infinity and infinity to d, and it's not hard to check that g is its own inverse. So g(f(z)) is an analytic injective function that fixes its infinity. That means we can ignore infinity, and think of it as an analytic injective function on the complex plane, which you already know means g(f(z)) = az+b. So f(z) = g(g(f(z))) = g(az+b). Play around with this, and what you'll get are precisely the Mobius transformations.--203.97.79.114 (talk) 03:03, 31 October 2010 (UTC)

Thankyou, that's a great help! Estrenostre (talk) 12:01, 31 October 2010 (UTC)

Lie Groups and Infinitesimal Actions

I'm reading a paper about projective differential geometry. There is a smooth surface in the real projective space RP³, and the authors say that the group PGL(4,R) acts on RP³. That's what projective differential geometry looks at: differential invariants under the action on projective transformations. They claim that the Lie algebra $\scriptstyle {\mathfrak {sl}}(4,{\mathbf {R} })$ is the "infinitesimal version of the PGL(4,R)-action." Are they trying to say that the tangent space to PGL(4,R) at the identity is SL(4,R)? I always thought that the tangent space to SL(n,R) at the identity was the space of n-by-n matrices with zero trace. If the tangent space to SL(n,R) at the identity is different to SL(n,R) it means, in some sense, that SL(n,R) is not linear. So how can SL(4,R) be the tangent space to PGL(4,R) at the identity when SL(4,R) is not linear? — Fly by Night (talk) 18:05, 31 October 2010 (UTC)

Here's a link to the article in question. — Fly by Night (talk)

The question is confused because you use lower case sl for the Lie algebra in only one place, when you should use it in several. The point is that PGL and SL are infinitesimally the same, equivalently, (they're semisimple) they have the same global universal cover or the same quotient by their centers. Their lie algebras are the traceless 4x4s: sl is the subspace of gl with zero trace, pgl is the quotient of gl by the diagonal) John Z (talk) 00:06, 1 November 2010 (UTC)

That's why I'm making a post on the reference desk: I, myself, am confused by it all. The paper tells me that they're infinitesimally the same. I was hoping someone could explain why, and what it means. — Fly by Night (talk) 10:49, 1 November 2010 (UTC)

Starting with lie group morphisms SL->GL->PGL and taking the tangent space at the identity, the lie algebra, we get sl-->gl-->pgl, which is an isomorphism of lie algebras sl & pgl, so sl is the "infinitesimal version of PGL(4,R)" . SL being a tangent space of PGL doesn't make sense, capital SL is a lie group, not a vector space (with lie algebras structure) like sl.John Z (talk) 04:20, 2 November 2010 (UTC)

Incorrectly named theorems

It is often, rather cynically, remarked in mathematics that a theorem is named after the last person to discover it, hence denying its original discoverer of recognition, such as the Steinitz exchange lemma. This law is named after a person, who attributes it to someone else, but I cannot for the life of me remember who. Anyone know? Thanks. 128.232.247.49 (talk) 22:02, 31 October 2010 (UTC)

I've heard the name you're referring to but I can't come up with it at the moment. However the general principle that what counts is not the first person to discover it, but rather the last, is called the Columbus principle. I used to think it was an injustice but I don't anymore. If you discover something and then someone discovers it again later, it means you did not succeed in adding your knowledge to the general heritage of mankind, so why should you get credit for it? --Trovatore (talk) 22:26, 31 October 2010 (UTC)

Stigler's law of eponymy. Algebraist 22:32, 31 October 2010 (UTC)

Trovatore: Technological, political and religious factors can all influence the dissemination of knowledge. Controversial, hypothetical example: You were a political prisoner/prisoner of war and your work was never released until many years after the down fall of the regime that held you prisoner. By which time, another mathematician had used all of the freely available work to arrive at your conclusion. Albeit some years later. I would say that you deserve all the credit, and then some. — Fly by Night (talk) 22:38, 31 October 2010 (UTC)

Also,it may also happen that at the time of the first discovery people is simply not ready to it, and many years are needed in order that they get acquainted to it. For instance, think to Paolo Ruffini's work on the impossibility of solving the quintic by radicals . In 1799 he proved the theorem up to a minor gap, that himself or somebody else could have fixed soon, had his book met the attention that deserved. But times were not ready for a such a revolutionary idea as proving the impossibility; 20-30 years later, this idea had slowly spread and become more natural, and Abel and Galois got more lucky (at least, on the publishing side). --pma 00:30, 1 November 2010 (UTC)

Yes, sometimes the dog really does eat your homework. So what? You weren't the one who made the contribution to human knowledge. --Trovatore (talk) 01:00, 1 November 2010 (UTC)

:-) Who knows who are the ones? Often, it is really difficult to weigh the impact of a contribution, that can be quite delayed in time. But I get your point; science is not a solitary game, and a discovery really makes a contribution if it is followed. --pma 09:25, 1 November 2010 (UTC)

Sorry to cut the tangential philosophizing short, but to answer the original question, the phenomenon is known as Stigler's law of eponymy, or sometimes Boyer's law. —Bkell (talk) 00:43, 1 November 2010 (UTC)

This thread exhibits why StatisticsMan's law of indenting is so important. I realize that Algebraist was replying to the OP so he indented the same as Trovatore, who had already replied. But, it just looks as if Algebraist's remark is part of the reply by Trovatore. I actually missed it (and noticed it when I had read through half of this topic) and it looks like Bkell did the same thing since he answered the question that had already been answered. I just put an extra line break in there and now it looks separate. That's my law of indenting. StatisticsMan (talk) 17:04, 1 November 2010 (UTC)

Oh, yeah, oops. Good catch. —Bkell (talk) 18:24, 1 November 2010 (UTC)

See also the Mathoverflow thread What are examples of mathematical concepts named after the wrong people? (Stigler’s law). – b_jonas 19:24, 1 November 2010 (UTC)

November 1

Trying to solve calculus problems using the Chain Rule

So, I'm not too sure how to do the whole Chain Rule thing using either of the notations (dy/dx or FOG). I'm trying to do stuff myself. Can you help me with this problem? f(x) = (6x-5)⁴. The book says the answer is (24x-5)³. But... why? Thank you. —Duncan^{What I Do} / _{What I Say} 01:21, 1 November 2010 (UTC)

I assume the problem is to take the derivative? If so, (24x-5)³ is not the correct answer. Are you sure the problem isn't 6(x-5)⁴ and the answer 24(x-5)³?

For the chain rule, you need to think of the function as having an inside and an outside. Working with (19x+1)⁵ as an example, the inside is 19x+1, and the outside is ( )⁵. You start by taking the derivative of the outside: the derivative of ( )⁵ is 5( )⁴. Then you plug the inside back into that: 5(19x+1)⁴. Then you multiply by the derivative of the inside: 19*5(19x+1)⁴.--130.195.2.100 (talk) 02:39, 1 November 2010 (UTC)

To understand the Chain Rule in relation to the work presented immediately above by 130.195.2.100, see Example II. Dolphin (t) 03:06, 1 November 2010 (UTC)

According to the chain rule,

${\frac {d}{dx}}(6x-5)^{4}=4(6x-5)^{3}\cdot 6,$

But you haven't told us what the question was! Michael Hardy (talk) 04:12, 1 November 2010 (UTC)

Yes! The question says, take the derivative of y=(6x-5)^4, and the answer is f'(x)=24(6x-5)^3. —Duncan^{What I Do} / _{What I Say} 05:01, 1 November 2010 (UTC)

You may or may not find the following symbol-pushing useful:

${\frac {dy}{dx}}={\frac {d[(6x-5)^{4}]}{dx}}={\frac {d[z^{4}]}{dx}}\,\,\,({\text{where }}z=6x-5)$

$={\frac {d[z^{4}]}{dz}}\times {\frac {dz}{dx}}=4z^{3}\times {\frac {d[6x-5]}{dx}}=4z^{3}\times 6=4(6x-5)^{3}\times 6=24(6x-5)^{3}$

The "key step" is the one going from the end of the first line to the beginning of the second line. It's the chain rule:

${\frac {d[z^{4}]}{dz}}\times {\frac {dz}{dx}}={\frac {d[z^{4}]}{\cancel {dz}}}\times {\frac {\cancel {dz}}{dx}}={\frac {d[z^{4}]}{dx}}$

Informally and very non-rigorously, the chain rule can be stated as "the $dz$'s cancel". 67.158.43.41 (talk) 07:11, 1 November 2010 (UTC)

Any introduction to the Chain Rule, using a question like this one, can be made clearer by beginning with a change of variable:

Let $u=(6x-5)$ and therefore ${\frac {du}{dx}}=6$

The question then becomes: If $y=u^{4}$ find ${\frac {dy}{dx}}$

${\frac {dy}{du}}={\frac {d}{du}}(u)^{4}=4(u)^{3}$

The Chain Rule can be expressed as:

${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$

${\frac {dy}{dx}}=4(u)^{3}\cdot 6=4(6x-5)^{3}\cdot 6,$

${\frac {d}{dx}}(6x-5)^{4}=24(6x-5)^{3}$ Dolphin (t) 07:25, 1 November 2010 (UTC)

Or, shortly and painlessly: d(6x-5)⁴=4(6x-5)³d(6x-5)=4(6x-5)³6dx=24(6x-5)³dx. Bo Jacoby (talk) 08:32, 1 November 2010 (UTC).

Counterexamples & L'Hopital

If I'm not mistaken, proofs of L'Hopital's rule usually rely on the mean value theorem. So suppose we're in a field like Q in which the MVT does not hold. Are there counterexamples to L'Hopital in such cases? Michael Hardy (talk) 04:14, 1 November 2010 (UTC)

There are. The basic idea is that functions on R with jump discontinuities are still continuous on Q with the standard metric topology if the jumps happen at irrational points. For example define f:Q → R by f(x) = π/n for π/(n+1) < x < π/n and f(0) = 0. This function is continuous on Q. Let g(x) = x. Then $\lim _{x\to 0}f(x)=\lim _{x\to 0}g(x)=0$ and f'(x)/g'(x) = 0 for all x, but $\lim _{x\to 0}f(x)/g(x)=1$. Rckrone (talk) 05:50, 1 November 2010 (UTC)

Looks like that works. Except maybe you'd want f(x) = 1/n for π/(n+1) < x < π/n, with 1 rather than π in the numerator of the value of the function, so that it would be rational-valued. Let's see....that would make the limit 1/π. If we want the limit to be rational as well, then maybe there's more work to do? Michael Hardy (talk) 15:38, 1 November 2010 (UTC)

You could replace π/n with a rational approximation to it. If you use good enough approximations, the limit will still be 1. Algebraist 17:15, 1 November 2010 (UTC)

So they'd have to be succesively better approximations as one approaches x. Michael Hardy (talk) 19:50, 1 November 2010 (UTC)

Did you mean, as x approaches 0? This is of course easy, you can use $f(x)=4\sum _{i=0}^{n}{\frac {(-1)^{i}}{(2i+1)n}}$ for π/(n+1) < x < π/n. -- Meni Rosenfeld (talk) 09:30, 3 November 2010 (UTC)

Yes, that's what I meant. Thank you Rckrone, Algebraist, and Meni Rosenfeld. Michael Hardy (talk) 00:10, 5 November 2010 (UTC)

Question

What is the statistical likelyhood of humans (Homo sapiens sapiens) having done all unique actions —Preceding unsigned comment added by Deliciousdreams444 (talk • contribs) 16:38, 1 November 2010 (UTC)

Zero. —Bkell (talk) 18:22, 1 November 2010 (UTC)

50%: Either they have or they haven't. 84.153.204.6 (talk) 18:28, 1 November 2010 (UTC)

No human has infrumppeltated a hynosterous yet, despite there being millions of them on the as-yet undiscovered planet Zargastion. 92.29.115.229 (talk) 11:30, 2 November 2010 (UTC)

The word 'done' is ill-defined, due to special relativity 70.26.152.11 (talk) 23:46, 2 November 2010 (UTC)

November 2

Decimals in Fractions

Is it acceptable to have decimals in fractions? e.g., 2.13/4.7 I thought I remembered learning somewhere that even a non-simplified fraction must not contain decimals, a custom just as conventional as not dividing by zero. Can't find any sources one way or the other now. (Google search) 72.164.134.59 (talk) 00:54, 2 November 2010 (UTC)

There's nothing wrong with that; the expression 2.13/4.7 just means 2.13 divided by 4.7. By the way, it isn't just "conventional" that division by zero is undefined—if you tried to give it a meaningful value you would find that arithmetic doesn't work the way you want it to. —Bkell (talk) 03:50, 2 November 2010 (UTC)

I disagree that division by zero is not a convention. We could easily do all math on the Riemann sphere if we so chose. 70.26.152.11 (talk) 23:45, 2 November 2010 (UTC)

I disagree. I'm all for using the Riemann sphere, or the real projective line. You might have a case that working mostly with real numbers rather than these compactifications is a convention. I'm not so sure about the "easily" - the rules of arithmetic there have quite a few caveats relative to reals. The impossibility of division by zero in reals, and the peculiarities of the structures which allow it, result from the very nature of division and of zero. Comparing it with grade school teacher whims like using only integers in fractions is downright insulting. -- Meni Rosenfeld (talk) 09:23, 3 November 2010 (UTC)

Division by zero being undefined is "conventional" inasmuch as every definition is at some level simply a convention. However, I would say calling division by 0 "conventional" breaks the connotations of the word, particularly that conventions are usually small notational conveniences, and that division by zero is not in the same league of simplicity as writing fractions with whole numbers. 67.158.43.41 (talk) 09:53, 3 November 2010 (UTC)

It's sometimes odd not to simply convert a decimal divided by something into a single decimal, perhaps rounding depending on how you're handling the significant figures. Fractions are sometimes written as a/b for whole numbers a and b to preserve their meaning or accuracy. For instance, if I said the probability of rolling 1 three times in a row with a fair die is about 0.00462963, that's much less accurate and less elucidating than 1/216. As a rule of thumb, decimals don't tend to have such nice combinatorial interpretations--they're just numbers, so you may as well write them as such. 67.158.43.41 (talk) 04:38, 2 November 2010 (UTC)

And of course if you decide you don't want the decimals, you can always multiply top and bottom by a suitable factor of ten. EG 213/470. -- SGBailey (talk) 10:32, 2 November 2010 (UTC)

Or perhaps even a power of ten. -- 119.31.126.67 (talk) 11:32, 2 November 2010 (UTC)

yeah. -- SGBailey (talk) 21:56, 2 November 2010 (UTC)

Dice Probability

If I roll P (ordinary 6-sided) dice, and my opponent rolls Q similar dice, what are the odds of me a) winning? b) drawing with him?

Not homework, I'm trying to improve my playing of Dicewars

 Rojomoke (talk) 14:33, 2 November 2010 (UTC)

What is the rule for determining the winner?—Emil J. 14:42, 2 November 2010 (UTC)

First, I assume by `winning' you mean rolling a higher sum of pips. In any case, it will be easier to think of your answer as a probability rather than odds. The general result can be worked out as follows. What is the expected_value of one D6?(Hint, it is not 3, you can follow the worked example on our expected value article) By linearity of the mean, the expected value of the sum is the sum of expected values. If you want to get good at dicewars, you should invest the time to finish it off from here yourself :) SemanticMantis (talk) 14:47, 2 November 2010 (UTC)

I think you should first look at Dice#probability, from which the answer can be derived. The answer should be the probability the roll of (P + Q) dice is greater than 6Q. E.g. if you have two dice, your opponent has one, P + Q is 3, and the chance of you winning is the same as rolling over six with these three dice. A roll of exactly six would be a draw. And so on.--JohnBlackburne^words_deeds 14:51, 2 November 2010 (UTC)

John, I think your description only works for the probability of an assured win, i.e. no roll of Q can beat the the given roll of P. If this is the win condition of dicewars, fine, but otherwise the OP should consider theconditional_probability for a case-by-case analysis. You'll end up getting the probability of winning by summing over all conditional winning probabilities, conditioned on of each throw of Q dice.SemanticMantis (talk) 14:57, 2 November 2010 (UTC)

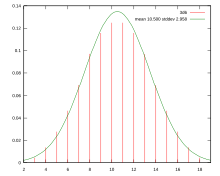
My math was a bit wrong. It should be the probability (P+Q) dice is more than 7Q, or equal for a draw.--JohnBlackburne^words_deeds 15:19, 2 November 2010 (UTC)

E.g. consider the simplest case, 2 dice vs. 1 die. You win if the score of your two dice is greater than your opponents one. The distribution of the probability of (your roll - his roll) will look like the graph on the right, except instead of going from 2 to 18 it goes from -5 to 11, so is shifted by seven. You win if your winning margin is greater than zero, equivalent to seven on this graph. You shift by seven for every dice your opponent has, hence the 7Q (you may have to click through to see it, the SVG to PNG converter doesn't seem to be working right now).--JohnBlackburne^words_deeds 15:30, 2 November 2010 (UTC)

I think that the assumption that the goal is to have the sum of your dice exceed the opponents dice is wrong. Looking at the game, it appears to be designed like Risk. You roll your dice. The opponent rolls his. Your highest value is compared to his highest value. The one with the lower value loses. Then, your next highest value is compared to his next highest value - and so on. Ties are considered a push - neither die is killed. -- kainaw™ 17:26, 2 November 2010 (UTC)

I don't think so (and I've played this game many times before). As far as I can tell it is totalling the two dice totals, and you win if your total is more than your opponents. If they are the same, or if your total is less, you lose as in you do not gain the territory. It's the numeric values of the totals that matter every time. Play it a lot and you get a feel for the probabilities, and the dice rolls do seem completely random, though the play isn't: they gang up on a stronger competitor, and will hold off attacking weaker ones, but won't hold off attacking you.--JohnBlackburne^words_deeds 18:14, 2 November 2010 (UTC)

If it's indeed the total that counts, then the probabilities of winning for P and Q from 1 to 10 (rounded to 1/10000) are:

0.4166	0.0925	0.0115	0.0007	0	0	0	0	0	0
0.8379	0.4436	0.152	0.0358	0.0061	0.0007	0	0	0	0
0.9729	0.7785	0.4535	0.1917	0.0607	0.0148	0.0028	0.0004	0	0
0.9972	0.9392	0.7428	0.4595	0.2204	0.0834	0.0254	0.0063	0.0013	0.0002
0.9998	0.9879	0.9093	0.718	0.4636	0.2424	0.1036	0.0367	0.0109	0.0027
0.9999	0.9982	0.9752	0.8839	0.6996	0.4667	0.2599	0.1215	0.0481	0.0163
1	0.9998	0.9946	0.9615	0.8623	0.6851	0.4691	0.2743	0.1373	0.0593
1	0.9999	0.999	0.9895	0.9477	0.8438	0.6734	0.471	0.2864	0.1515
1	0.9999	0.9998	0.9976	0.9833	0.9343	0.8278	0.6637	0.4727	0.2967
1	0.9999	0.9999	0.9995	0.9954	0.9763	0.9217	0.8137	0.6554	0.474

The probabilities for a draw are:

0.1666	0.0694	0.0154	0.0019	0.0001	0	0	0	0	0
0.0694	0.1126	0.0694	0.0248	0.0059	0.001	0.0001	0	0	0
0.0154	0.0694	0.0928	0.0654	0.0299	0.0098	0.0024	0.0004	0	0
0.0019	0.0248	0.0654	0.0809	0.0614	0.0326	0.013	0.004	0.001	0.0002
0.0001	0.0059	0.0299	0.0614	0.0726	0.0579	0.0339	0.0155	0.0057	0.0017
0	0.001	0.0098	0.0326	0.0579	0.0665	0.0548	0.0346	0.0174	0.0072
0	0.0001	0.0024	0.013	0.0339	0.0548	0.0617	0.0521	0.0347	0.0189
0	0	0.0004	0.004	0.0155	0.0346	0.0521	0.0578	0.0498	0.0346
0	0	0	0.001	0.0057	0.0174	0.0347	0.0498	0.0545	0.0477
0	0	0	0.0002	0.0017	0.0072	0.0189	0.0346	0.0477	0.0518

For example, if $P=3,\ Q=2$ there's a probability of 77.85% to win, 6.94% to draw and 15.2% to lose. -- Meni Rosenfeld (talk) 20:10, 2 November 2010 (UTC)

Meni's brute force calculation can be approximated by using the normal distribution like this.

1. The expected value of pips by throwing one dice is (1+2+3+4+5+6)/6 = 7/2.
2. The variance is ((1−7/2)²+(2−7/2)²+(3−7/2)²+(4−7/2)²+(5−7/2)²+(6−7/2)²)/6 = 35/12.
3. When you throw P dice the expected number of pips is 7P/2 and the variance is 35P/12.
4. When your opponent throw Q dice the expected number of pips is 7Q/2 and the variance is 35Q/12.
5. You are ahead by X pips which is of course an integer.
6. The expected value of X is μ = 7(P−Q)/2 pips but the variance is σ² = 35(P+Q)/12.
7. You win when X>1/2 and you draw when −1/2<X<1/2.
8. The variable (X−μ)/σ has expected value 0 and variance 1 and is approximately normally distributed.

a) The approximate probability of winning is $\operatorname {Q} \left({\frac {{\frac {1}{2}}-\mu }{\sigma }}\right)={\frac {1+\operatorname {erf} (3N)}{2}}$

b) The approximate probability of drawing with him is $\operatorname {Q} \left({\frac {-{\frac {1}{2}}-\mu }{\sigma }}\right)-\operatorname {Q} \left({\frac {{\frac {1}{2}}-\mu }{\sigma }}\right)={\frac {\operatorname {erf} (4N)-\operatorname {erf} (3N)}{2}}$

where $N={\frac {P-Q}{P+Q}}{\sqrt {6{\frac {P+Q}{35}}}}$ and the error function erf is used for computing the Q-function.

Meni's example, P=3 and Q=2, gives that the approximate probability of winning is (1+erf((3 sqrt(6/7))/5))/2 = 0.7839, and the approximate probability of drawing is (erf((4 sqrt(6/7))/5)-erf((3 sqrt(6/7))/5)))/2 = 0.0686 (computed by http://www.wolframalpha.com ).

These approximations are close to Meni's results, even if P and Q are small numbers. Bo Jacoby (talk) 10:40, 3 November 2010 (UTC).

Thanks to Taemyr for improving the above text. I continued the improvement. Bo Jacoby (talk) 23:20, 3 November 2010 (UTC).

Johns answer further up is correct. Let Dice(X) denote a result from rolling X dices. Since the probability distribution of Dice(X) is symetric with min X and max 6*X we have that Dice(1) has the same probability distribution as 7-Dice(1), more importantly Dice(X) has the same probability distribution as 7*X-Dice(X).

The result we are looking for is Dice(P)-Dice(Q)>0.

By the above Dice(P)-Dice(Q) will have the same probability distribution as Dice(P)-(7*Q-Dice(Q))=Dice(P)+Dice(Q)-7

Hence we are looking for the probability of getting more than 7*Q on all dices involved.

Taemyr (talk) 19:01, 3 November 2010 (UTC)

Use this matrix identity??

It can be shown that ${\begin{bmatrix}0&1\\-1&0\end{bmatrix}}^{2}=-{\begin{bmatrix}1&0\\0&1\end{bmatrix}}.$ Use this matrix identity to simplify $\left(-{\frac {1}{2}}{\begin{bmatrix}1&0\\0&1\end{bmatrix}}+{\frac {\sqrt {3}}{2}}{\begin{bmatrix}0&1\\-1&0\end{bmatrix}}\right)^{3}$
It can of course be done from scratch but how do you use the matrix identity?--115.178.29.142 (talk) 21:39, 2 November 2010 (UTC)

I can interpret the instructions two different ways. I think the second way makes more sense. (1) You can use the distributive law to expand and simplify the expression you are given. When you do this, you will multiply the matrix ${\begin{bmatrix}0&1\\-1&0\end{bmatrix}}$with itself, so you can use the given matrix identity to simplify this. (2) The matrix identity draws attention to a particular property of that matrix, namely, that it's square is -1. Use this insight to find a clever way to simplify the given expression. Eric. 82.139.80.73 (talk) 21:55, 2 November 2010 (UTC)

I probably should give a slightly bigger hint. What more familiar number has a square of -1? Then keep in mind that what is important about a number is not how you write it down or whether you call it a "matrix" or whatnot, but how it behaves. Eric. 82.139.80.73 (talk) 22:20, 2 November 2010 (UTC)

$\left(-{\frac {1}{2}}{\begin{bmatrix}1&0\\0&1\end{bmatrix}}+{\frac {\sqrt {3}}{2}}{\begin{bmatrix}0&1\\-1&0\end{bmatrix}}\right)^{3}=\left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)^{3}=\left(e^{\frac {2\pi i}{3}}\right)^{3}=e^{2\pi i}=1={\begin{bmatrix}1&0\\0&1\end{bmatrix}}$ Thanks!--115.178.29.142 (talk) 22:39, 2 November 2010 (UTC)

I agree that this answer is true, but it is debatable whether it is sufficient. Handwavy arguments about "how it behaves" are tricky: be careless, and you might end up proving $i=-i$ because they behave the same. For example, here's a naive objection: matrix multiplication is not in general commutative -- are you sure that the properties of C you use in your calculation depend only on $i^{2}=-1$ but not $ab=ba$? If I were marking the answer, I'd expect some sort of explicit argument that an appropriate set of matrices are isomorphic to C, as justification of moving back and forth between them.

(Also, I think it sounds strange to be asked to "simplify" an expression with no variables in it. Usually one would simply speak of "evaluating" it). –Henning Makholm (talk) 23:25, 2 November 2010 (UTC)

Right. My goal was more to intuitively motivate the answer, but to formally justify this we would do something like embed C in the ring of two-by-two real matrices in the appropriate way. Of course by that point, it's easier to just do the computations. Hopefully the OP will not handwave on the actual set. Eric. 82.139.80.73 (talk) 07:28, 3 November 2010 (UTC)

Personally, I'd accept a very brief justification if I were grading. Something like...

"We see

${\begin{bmatrix}a&b\\-b&a\end{bmatrix}}{\begin{bmatrix}c&d\\-d&c\end{bmatrix}}={\begin{bmatrix}ac-bd&ad+bc\\-(ad+bc)&ac-bd\end{bmatrix}}$

so a subset of 2x2 real matrices is [ring] isomorphic to C (the additive isomorphism is trivial). Therefore... (insert above string of equalities here)"

It lets me (grader) know you (student) know what's going on without wasting my time with a long-winded but very easy argument. I think this would be faster for me than cubing the above directly, if I had instantly noticed the isomorphism. If the argument were at all unusual or difficult, more justification would be appropriate. (It seems to me the OP could trivially come up with the subset, otherwise I wouldn't have implied it.) 67.158.43.41 (talk) 09:45, 3 November 2010 (UTC)

For this specific calculation you really only need to go so far as to note that ${\begin{bmatrix}0&1\\-1&0\end{bmatrix}}$ and ${\begin{bmatrix}1&0\\0&1\end{bmatrix}}$ commute, which is obvious since the identity commutes with everything. Rckrone (talk) 04:44, 4 November 2010 (UTC)

You mean to apply the binomial theorem, since the terms commute? Perhaps that would be quicker; uglier, I'd say, but less writing--two lines, if you're terse. 67.158.43.41 (talk) 16:43, 4 November 2010 (UTC)

No I don't mean to explicitly write out the terms of the expansion. Once you address commutativity (or alternatively note that the expression is a polynomial in ${\begin{bmatrix}0&1\\-1&0\end{bmatrix}}$) then there are no obstacles to treating that matrix (in this calculation) as if it were the imaginary unit. Rckrone (talk) 22:29, 4 November 2010 (UTC)

Peano axioms

In a weakened version of the Peano axioms without multiplication, is it still possible to express the formula x=yz? Would these axioms be Gödel-incomplete, or is multiplication necessary to state any unprovable propositions? In the Peano axioms with multiplication, is it possible to express x=y^z? 70.26.152.11 (talk) 23:53, 2 November 2010 (UTC)

A formalization of one such weakened arithmetic is called Presburger arithmetic. In such a system, for free variables x, y, and z, it is not possible to express the relation x=y*z. If multiplication by a constant is used as shorthand for repeated addition, so that y+y=2*y, then it is possible to express for free variables x and y that x = y+y = 2*y. The article describes details of decidability in this system. Black Carrot (talk) 01:03, 3 November 2010 (UTC)

Thanks, that's exactly what I was looking for. 70.26.152.11 (talk) 04:02, 3 November 2010 (UTC)

For the second question: Yes, because integer exponentiation is primitive recursive and Gödel showed that every primitive recursive function is definable in the Peano arithmetic. This makes use of a trick (Gödel's β function) to quantify over all finite sequences of integers with finitely many quantifiers. –Henning Makholm (talk) 06:48, 3 November 2010 (UTC)

In Peano arithmetic#Arithmetic, it says "Addition is the function + : N × N → N (written in the usual infix notation), defined recursively as:" Should "N × N" be "N + N" ? -- SGBailey (talk) 10:10, 3 November 2010 (UTC)

No. The × denotes cartesian product: N × N is the set of ordered pairs of natural numbers. I've no idea what your "N + N" could mean. Algebraist 10:16, 3 November 2010 (UTC)

My only guess is that they took the "recursive" definition in a very non-standard way, thinking to use + inside it's domain's definition. I'm curious, what did you mean by "N + N", SGBailey? (I don't mean to call out a mistake; I'm genuinely curious what you were thinking, even if you don't believe it anymore.) 67.158.43.41 (talk) 12:41, 3 November 2010 (UTC)

Both Addition and Multiplication weredefined as "N × N" and it just seemed unlikely to me that they'd be the same. -- SGBailey (talk) 16:04, 3 November 2010 (UTC)

They are not defined as "NxN" they are both defined as functions "N x N → N". Meaning they are both functions that take two natural numbers and return one natural number, and so far they are the same. The definition then goes on with "defined recursivly as:" and the stuff after that tells us the difference between + and *. Taemyr (talk) 17:13, 3 November 2010 (UTC)

Perhaps you're sort of confusing the notation $n\mapsto n+n$ with the notation $+:N\times N\rightarrow N$, which are superficially similar, but mean very different things. The second notation has the meaning Taemyr describes, where the N x N part is specifying the domain of the function and the N is specifying the codomain, with the arrow being the conventional delimiter between the two. This notation also explicitly names the function using the symbol "+", where the colon is another delimiter between the function name and the domain. In more formal usage one applies + like any function, i.e. with +(n, m). The first notation is describing a (so far anonymous) function mapping n to twice n. The domain and codomain aren't specified. This is less formal but often clearer when context supplies the domain, codomain, and definition of any symbols used (like +, which must already be defined for the first notation to make sense).

Thanks for satisfying my curiosity. I find it helpful for future explanations to hear a variety of misconceptions. Misconceptions also often give an interesting new perspective on things, which can sometimes be repaired to give real insight. 67.158.43.41 (talk) 18:08, 3 November 2010 (UTC)

It's interesting to note that the two notations mentioned by 67 are usually used together. For example, the real function that squares any number can be given the name f rigorously and concisely using the notation $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto x^{2}$. -- Meni Rosenfeld (talk) 19:56, 3 November 2010 (UTC)

Though if you've the function a name, it's just as easy to write $f\colon \mathbb {R} \to \mathbb {R} ,\ f(x)=x^{2}$.—Emil J. 12:24, 4 November 2010 (UTC)

In similar contexts N + N can mean the disjoint union of two copies of N. Doesn't make much sense here, though.—Emil J. 13:36, 3 November 2010 (UTC)

The disjoint union of two copies of one set works only for the empty set, so the number of applications for that seems to be very limited. I've seen (and usually) use $M\uplus N$ for the disjoint union of N and M. --Stephan Schulz (talk) 17:28, 3 November 2010 (UTC)

Any two sets have a disjoint union, whether or not the sets are disjoint, or even different. Disjoint union means the union of disjoint copies of the original sets, constructed for the purpose. Algebraist 17:36, 3 November 2010 (UTC)

Aha! I was only aware of the second definition in the article. Thanks. --Stephan Schulz (talk) 18:13, 3 November 2010 (UTC)

November 3

Sums of random variables, and line integrals

The setting is: Let $X$ and $Y$ be independent random variables (on the reals), with density functions $f_{X}$ and $f_{Y}$. The standard result for the density of $X+Y$ is $f_{X+Y}(a)=\int f_{X}(a-t)f_{Y}(t)dt$. I'm trying to derive this formula by using a line integral, but I'm getting a different result, so I must be doing something wrong.

This is my reasoning: The joint density of $(X,Y)$ on $R^{2}$ is given by $f_{X,Y}(a,b)=f_{X}(a)f_{Y}(b)$. To find $f_{X+Y}(a)$ we should integrate $f_{X,Y}$ over the line $x+y=a$. We can parametrize this line by the function $r:R\rightarrow R^{2},r(t)=(a-t,t)$. Note that $dr/dt=(-1,1)$, so $|dr/dt|={\sqrt {2}}$. Now if we calculate the line integral (as in Line_integral#Definition), we get $f_{X+Y}(a)=\int f_{X,Y}(r(t))|dr/dt|dt=\int f_{X,Y}(a-t,t){\sqrt {2}}dt=\int f_{X}(a-t)f_{Y}(t){\sqrt {2}}dt$. If we compare this with the textbook result above, then my result has a factor ${\sqrt {2}}$ that is not supposed to be there. Where did I go wrong? Arthena^(talk) 10:03, 3 November 2010 (UTC)

The problem is in the assumption that the line integral gives the desired result. Let's say we want to find the probability that $X+Y\in (a-\epsilon ,a+\epsilon )$. This is given by the integral over the region $a-\epsilon <X+Y<a+\epsilon$. This region has a thickness of $\epsilon {\sqrt {2}}$, so the integral over it is equal to the line integral times $\epsilon {\sqrt {2}}$. However, by assuming that the line integral will give the density, you have implied that the probability will be the line integral times $2\epsilon$ (the density times the interval length). So you'll need to multiply by a correction factor equal to the thickness of the line divided by the corresponding length of the interval of the derived variable.

Because this can be confusing, it's best to use the cumulative density wherever possible. -- Meni Rosenfeld (talk) 12:03, 3 November 2010 (UTC)

Thanks for the answer. Arthena^(talk) 23:38, 3 November 2010 (UTC)

Interpolation on the surface of a sphere

I want to to interpolate along a great circle between two points on the surface of a sphere expressed in polar coordinates as (φ_s, λ_s) and (φ_f, λ_f), with the interpolated point also expressed in polar coordinates as (φ_i, λ_i).

I'm doing this in code, and the best I've come up with is to:

1. Interpret each point as Euler angles (φ, λ, 0.0)
2. Convert the Euler angles to quaternions and use spherical linear interpolation to get an interpolated quaternion Q_i
3. Convert Q_i to Euler angles
4. Interpret the Euler angles as the interpolated point.

My questions would be: is this complete nonsense, and is there a simpler, or more direct, way of going about it?

78.245.228.100 (talk) 11:46, 3 November 2010 (UTC)

For an alternative, how about simply converting your start and end points to Cartesian and taking a linear interpolation of the resulting vectors, converting back to spherical when you want? You could do this symbolically as well; who knows, maybe there are some significant simplifications (though I don't hold out much hope). Seems way simpler than trying to run through Euler angles and quaternions. 67.158.43.41 (talk) 12:38, 3 November 2010 (UTC)

If I convert to 3D Cartesian and interpolate linearly I not only deviate from the great circle, but I end up tunelling through the sphere. 78.245.228.100 (talk) —Preceding undated comment added 12:44, 3 November 2010 (UTC).

Sorry, I had meant to say, "interpolate and normalize", though then a linear interpolation of the cartesian vectors is a nonlinear interpolation on the surface. However, making the interpolation linear wasn't a requirement in the OP. If it should be, the correction term for the interpolation speed shouldn't be too hard to derive geometrically with a little calculus. You would have to special-case angles larger than 180 degrees as well. Hmm... that special case makes this not nearly as nice as I thought at first. However, after normalizing, you do not deviate from a great circle, since great circles lie in planes running through the sphere's center, which any linear combination of vectors in that plane also lie in.

An alternative would be to use a linear map to send the start and end vectors to (1, 0, 0) and (0, 1, 0) with their normal (unit cross product) getting sent to (0, 0, 1). The vectors $(\cos(\theta ),\sin(\theta ),0)$ for $0\leq \theta \leq \pi /2$ would correspond to the points of interpolation on a sphere. The inverse of the linear map so defined would convert back. I like this method better, since the inverse operation has a very simple form.

Edit: you would have to normalize in this case as well, or you could send the end vector to $(\cos(\phi ),\sin(\phi ),0)$ where $\phi$ is the angle between the start and end vectors, which is the inverse cosine of their dot product, or 2pi minus that for interpolations longer than 180 degrees. The upper limit of $\theta$ is then $\phi$. The inverse is slightly more complicated in this case.

Further edit: if my algebra is right, the final interpolation is simply

$(\cos(\theta ),\sin(\theta ),0)=c_{1}(1,0,0)+c_{2}(\cos(\phi ),\sin(\phi ),0)\mapsto c_{1}\mathbf {s} +c_{2}\mathbf {e}$

$=(\cos(\theta )-\sin(\theta )\cot(\phi ))\mathbf {s} +\sin(\theta )\csc(\phi )\mathbf {e}$

where s is the start vector, e is the end vector, theta and phi are as above. The singularities of this conversion occur at phi=0 or pi, exactly where they should. Sorry for all the edits; I'm alternating this with doing something deeply tedious.... 67.158.43.41 (talk) 13:24, 3 November 2010 (UTC)

(edit conflict) To implement your interpolate/normalize with constant speed, write $\gamma :={\hat {s}}\cdot {\hat {f}}$ and $\delta :={\hat {s}}\cdot {\hat {\imath }}$, where ${\hat {\imath }}$ is the result. Then define the unnormalized ${\vec {\imath }}=t{\hat {s}}+(1-t){\hat {f}}$ and observe that $\delta ={\frac {{\hat {s}}\cdot {\vec {\imath }}}{\sqrt {{\vec {\imath }}\cdot {\vec {\imath }}}}}={\frac {t+(1-t)\gamma }{\sqrt {t^{2}+(1-t)^{2}+2t(1-t)\gamma }}}$. Solving gives $t={\frac {(\gamma -1)(\gamma +\delta ^{2})-\delta {\sqrt {(\gamma ^{2}-1)(\delta ^{2}-1)}}}{(\gamma -1)(\gamma +2\delta ^{2}-1)}}$ (I think this is the correct branch for all $\delta ,\gamma$). Then the algorithm is just to take $\theta \rightarrow \cos \theta =\delta \rightarrow t\rightarrow {\vec {\imath }}\rightarrow (\phi _{i},\lambda _{i})$. --Tardis (talk) 15:00, 3 November 2010 (UTC)

I can't find it in an article, but what I would do is:

* find the quaternion that rotates one vector to the other.

* convert it to axis-angle form (alternately you can derive the axis and angle directly, but this is I think is clearer)

* interpolate the angle from 0 to the angle calculated

* generate a quaternion from the axis and interpolated angle, and use this to rotate the first of the vectors (the one rotated from in the first step)

the vector will move linearly along the great circle, i.e. at a constant speed along the surface, as the angle is interpolated linearly. The conversions to and from axis angle are at Rotation representation (mathematics)#Euler axis/angle ↔ quaternion. I can't find anywhere that gives the rotation between two vectors as a quaternion, but it's a straightforward result. --JohnBlackburne^words_deeds 13:40, 3 November 2010 (UTC)

Begging the question and differentiating e^x

Yesterday in class we were given a fairly simple assignment: show that ${\frac {d}{dx}}e^{x}=e^{x}$. This was supposed to illustrate something like the importance of rigourous proofs—the actual problem wasn't important and was in fact a problem from Calc 1. Oddly, a dispute arose over the problem nontheless. One of my classmates claimed that you can show ${\frac {d}{dx}}e^{x}=e^{x}$ by differentiating the Taylor series $e^{x}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+...$. I contested that this was begging the question because to know the Taylor series you have to know the derivative. She said that $e^{x}$ can be defined by its Taylor series, so this does not beg the question. Who is right? Thanks. —Preceding unsigned comment added by 24.92.78.167 (talk) 23:40, 3 November 2010 (UTC)

Hmm. It might be worth considering that you only need to know the derivative at $x=a$ to construct your Taylor series (in this case, $a=0$ and it's a Maclaurin series). An alternative way to get to the derivative of $e^{x}$ at $x=0$ (like, say, the basic definition of e) would remove the circularity ... --86.130.152.0 (talk) 00:09, 4 November 2010 (UTC)

No, you need to know all derivatives (first, second, third, ...) of $e^{x}$ evaluated at x=0 to construct the MacLaurin series. However, I support 24.92's classmate: You certainly can take the MacLaurin series as the definition of $e^{x}$, and I think this approach is found in several complex analysis texts. There are other reasonable options. You could define $e^{x}$ as the inverse of $\ln(x):=\int _{1}^{x}{\frac {1}{u}}du$; or you could define it as the unique function that is its own derivative and takes the value 1 at x=0. (My calculus text offers a choice between these two presentations.) Your assignment is ambiguous without a specified starting point, though presumably most people in the class knew what was expected. (But it's always good to stop and think about the assumptions you're making.) The fact that all of these approaches to defining $e^{x}$ are equivalent is a theorem, and your assignment was one step in the proof of that theorem. 140.114.81.55 (talk) 03:45, 4 November 2010 (UTC)

I'd agree with the OP in the sense that e^x's Maclaurin series was almost certainly a result of applying calculus to a different definition. That is, historically, the proof provided would very likely be circular. However, definitions can come out of thin air and if your class is using the Maclaurin series one the proof is correct for your purposes and not logically circular.

I really like the definition of the exponential function as the (unique) solution to the differential equation ${\frac {dy}{dx}}=y,y(0)=1$ as mentioned above. Yet another definition could take $e^{x+y}=e^{x}e^{y},e^{0}=(e^{x})'(0)=1$ which gives your result directly from the definition of the derivative. 67.158.43.41 (talk) 05:30, 4 November 2010 (UTC)

Since I don't see it quoted above, I'd like to make reference to this article. Pallida  Mors 08:32, 4 November 2010 (UTC)

November 4

Gödel numbering and second-order logic

Can first-order arithmetic quote-unquote "prove" any provable statement about second-order arithmetic through the use of Gödel numbering? If not, could the addition of the axiom "For all x, the set of numbers less than x is finite" be added to make any first-order statement provable, but only through the use of second-order intermediaries, leaving the system with only second-order Gödel sentences? 70.26.152.117 (talk) 01:14, 4 November 2010 (UTC)

It's very hard to answer your post; there are a lot of conceptual errors. I would suggest finding a reliable book on logic and working through it. Mendelson's textbook is very well regarded and discusses second-order logic as well as first-order logic. — Carl (CBM · talk) 01:35, 4 November 2010 (UTC)

graph automorphism

How do I show that for a simple graph G, Aut (G) is isomorphic to Aut(${\bar {G}}$), where ${\bar {G}}$ is the complement of G. I want to exhibit a isomorphism between them. But I cant seem to figure out that if I pick a permutation of the vertex set which preserves adjacency in G, what will be the corresponding permutation of the vertices which preserves adjacency in ${\bar {G}}$. -Shahab (talk) 07:24, 4 November 2010 (UTC)

Isn't it just the identity isomorphism? 67.158.43.41 (talk) 08:10, 4 November 2010 (UTC)

Oops!! Thanks.-Shahab (talk) 08:49, 4 November 2010 (UTC)

I have two more questions now. Won't the automorphism group of the complete bipartite graph K_m,n be S_m x S_n. I reason this out by taking the complement of K_m,n which is a disjoint union of K_m and K_n and trying to find its automorphism group. The automorphism groups of K_m and K_n are clearly S_m and S_n (sice adjacency is always preserved, no matter the permutation) and so to count all permutations I conclude that the automorphism group of K_m,n is S_m x S_n. But the wikipedia article says that there are 2m!n! automorphisms if m = n. Why is that so?

Secondly, I also want to compute the automorphism group of the Petersen graph which is the same as that of L(K₅). The wikipedia article says that it is S₅, the reason is not clear to me.

Thanks-Shahab (talk) 09:42, 4 November 2010 (UTC)

(Edit: ignore this; see next comment.) For your second question, a proof outline would be: (1) the inner "star" gets sent to itself in any automorphism (this is the hard part); (2) determining where the inner star gets sent determines where the outside vertices get sent, completely determining the permutation; (3) there are 5! = 120 permutations of the inner star, where each generates an automorphism, and these permutations are easily seen to be isomorphic to S_5. 67.158.43.41 (talk) 09:52, 4 November 2010 (UTC)

Both parts of your argument are false. There are automorphisms which (for example) swap the inner star with the outer pentagon, and the inner star (being a five-cycle) only has ten automorphisms in any case. A better way is to consider S₅ acting on the vertices of K₅ in the obvious fashion, which induces an action on the line graph of K₅, which induces and action on the Petersen graph. Algebraist 10:02, 4 November 2010 (UTC)

Thank you for pointing that out. I should be more careful in the future. I saw 5 vertices and 5! and shoved the ideas together, assuming the steps in the proof would necessarily follow. 67.158.43.41 (talk) 10:44, 4 November 2010 (UTC)

If m=n, then there are automorphisms of K_m,m which swap the left side with the right side. Thus the automorphism group is a semidirect product of S_m x S_m by Z₂. Algebraist 10:02, 4 November 2010 (UTC)

Thanks for the reply. For the first question instead of thinking about semi direct product (the part about Z₂ confuses me) can I just say: given any 2m symbols we can obtain a required automorphism by permuting the first m in m! ways and the second m in m! more ways. Hence we have is m!m! permutations. Moreover for each such permutation f we may also another permutation by mapping 1,...m to f(m+1)...f(2m), and mapping m+1,...2m to f(1),...f(m). This swaps the two complete graph vertices and as this is possible for each of our previous permutations so the total is 2m!m!. The second question is not clear to me still unfortunately. I am not understanding how and what group action is induced. I'll prefer an intuitive counting argument, if thats possible. That the complement of the Peterson graph is L(K₅) is clear to me and we hence need only to show Aut(L(K₅))=S₅.-Shahab (talk) 10:52, 4 November 2010 (UTC)

Here's how you may visualize the 5! automorphisms of the Petersen graph (if you like this algebraic way of thinking). You say you know that the Petersen graph is isomorphic to the complement of the line graph of K₅. Consider how the line graph is defined: the vertices of the line graph L(G) are the edges {x,y} of graph G, and two edges are connected iff they aren't disjoint. Take a permutation σ of the vertices of K₅ (there are 5! of these). This acts naturally on the edges of K₅, namely {x,y}σ is defined as {xσ,yσ} (here we use that we have the complete graph so we know the latter is also an edge). Now you can regard this permutation of the edges of K₅ as a permutation of the vertices of the line graph L(K₅). Prove that this permutation is a graph automorphism of the line graph. Also prove that no two of these permutations are equal.

(Incidentally, you can also generalize this to finding the n! automorphisms of the Kneser graph KG(n,k), where KG(n,2) is isomorphic to the complement of L(K_n).)

This does not give an easy way to prove that these are the only automorphisms of the graph, so you'll have to find some specialized argument for that. – b_jonas 20:26, 4 November 2010 (UTC)

Two questions

ok I have two questions: speaking of the prime-counting function $\pi (x)$ there is an approximation $\pi (x)\approx {\frac {x}{\ln x}}$ and $\pi (x)\approx li(x)$. Which is more accurate? Also, how can it be proven that $\lim _{n\to \infty }(1+{\frac {1}{n}})^{nx}=\lim _{n\to \infty }(1+{\frac {x}{n}})^{n}$? Thanks. —Preceding unsigned comment added by 24.92.78.167 (talk) 21:56, 4 November 2010 (UTC)

1. The latter
2. assuming x>0, substitute n=m/x in the left hand side

Bo Jacoby (talk) 22:56, 4 November 2010 (UTC).

Predicting the college football season

Let's say that:

• Oregon has a 59.2% chance to win every game before the BCS.
• Boise State has a 67% chance.
• Auburn has a 15% chance (noting they would have to play a conference championship).

In addition, either TCU or Utah may go undefeated, but not both, since they play each other. TCU has a 58% chance of beating Utah and a 99% chance of winning both of its other games, while Utah has a 42% chance of beating TCU and a 65.7% chance of winning all of its other games. That means, I'm guessing, that there is an 85% chance that either TCU or Utah will go undefeated.

Don't kill me over these percentages -- they come from a rankings website.

• What are the chances that no team among the above goes undefeated? (I'm guessing 1.7%)
• What are the chances that exactly one team goes undefeated (OR, Boise, Auburn or TCU/Utah)?
• What are the chances that exactly two teams go undefeated?
• What are the chances that exactly three teams go undefeated?
• What are the chances that exactly four teams go undefeated? (I'm guessing 5.1%)

Thanks -- Mwalcoff (talk) 03:13, 5 November 2010 (UTC)

One key assumption that should be explicitly stated is that the above percentages, unless otherwise stated, are independent probabilities, e.g., the chance of Boise winning is unaffected by what Oregon does. This may be approximately true, but may not hold if, for example, Boise was hoping for a Boise/Oregon grudge match in the finals, and as such is demoralized by an Oregon defeat. Anyway, it makes the calculations easier, so we'll assume it. Will also assume that when you ask for "three teams undefeated", your referring to three teams from those listed - that is, that some team not listed being undefeated doesn't count toward the three.

The probability of an event not happening is one minus the probability of it happening. The probability of two (probabilistically) independent events both occurring is simply the product of the independent probabilities. The probability of either of two mutually exclusive events occurring is simply the sum of the probabilities that either occurs. This is all we need to work out the probabilities.

So TCU has a .58*.99=.574 chance of being undefeated, while Utah has a .42*.657=.276 chance of being undefeated, which means that there's an .574+.276=.85 chance of either winning (since the two probabilities are mutually exclusive. For four teams undefeated, it's .592*.67*.15*.85=0.051. For no teams undefeated, it's (1-.59)*(1-.67)*(1-.15)*(1-.85)=.017 chance. The exactly one team defeated/undefeated is a little harder, but can be calculated with (prob.of only Oregon) + (prob. of only Boise) + ..., as each term is mutually exclusive (you can't have both Boise and Auburn be the only undefeated team). One team undefeated is .59*(1-.67)*(1-.15)*(1-.85) + (1-.59)*.67*(1-.15)*(1-.85) + (1-.59)*(1-.67)*.15*(1-.85) + (1-.59)*(1-.67)*(1-.15)*.85 = 0.161 and one team defeated (three teams undefeated) is (1-.592)*.67*.15*.85 + .592*(1-.67)*.15*.85 + .592*.67*(1-.15)*.85 + .592*.67*.15*(1-.85)=0.355 chance. Exactly two teams undefeated is a little harder, but becomes easier if we realize that we've exhausted all other cases - if it isn't no, one, three or four teams undefeated, it has to be two teams so 1-(.017+.161+.355+.051)=0.416 chance, as each sub-case is mutually exclusive. -- 174.21.240.178 (talk) 16:47, 5 November 2010 (UTC)

Calculus

How would one set up a calc equation to solve this. If the avg life expectancy of a person is some constant A, and their current age C, and the rate at which the life expectancy is extended be x, how would one set up a calculus equation to solve for the minimum value of x that would allow the person to live forever. Assuming that x is linear, I came up with something like t = (A-C) + (A-C)xdt, and then I would integrate and try to solve, but I don't think this is right. I think it would take the integral and not the derivative, but I am not even sure, as it has been quite a while since I have taken calculus. Can someone help me figure this out? I feel dumb for asking about this, as it should be a simple problem 98.20.180.19 (talk) 09:15, 5 November 2010 (UTC)

x is linear... in what? Time? I have difficulty interpreting your equation meaningfully, but maybe the answer is in there. If x is just a constant, then the minimum is x=1: each year a person lives, the average life expectancy must increase by at least 1 year to keep up with their growing age. In general, the rate of change of average life expectancy is a function x(t), you have initial average life expectancy of L(C) = A, so at any time the average life expectancy is given by the function

$L(t)=\int _{C}^{t}x(\tau )d\tau +A$

from the fundamental theorem of calculus. For x(t) = c, this simply becomes L(t) = c(t-C) + A. Your own age is just t, so you want L(t) - t > 0 always. If c < 0, L(t) is negative sometime, L(t) - t can't always hold. If c = 0, L(t) is a constant, which also won't work. If c >= 1, for A and C "reasonable" the equation does hold. For 0 < c < 1, L(t) grows more slowly than t, so L(t) - t is eventually negative, hence my statement above. 67.158.43.41 (talk) 10:51, 5 November 2010 (UTC)

If the population grows the average life expectancy could decrease and still have the possibility of a person living forever. I'm assuming life expectancy is calculated by seeing how long all the people lived who died in the current year. You might want to do something mor complex but you can't stick in an infinity for a person who's going to live forever! Dmcq (talk) 12:57, 5 November 2010 (UTC)

Actuaries already do these types of calculations, and have a standard terminology and notation for these concepts - see our articles on life table and force of mortality. Gandalf61 (talk) 13:33, 5 November 2010 (UTC)

Suggestions re learning LaTex, please?

Hi all. I think I need to finally spend the time to learn LaTex. My reasons for wanting to do so are:

• to allow me to document my self-study in symbolic logic, set theory, foundations, especially,
• to communicate effectively in online forums devoted to those topics,
• to send documents I've created about these topics (aka "homework" or "examples") via e-mail to professors or tutors, as yet unknown, and (ideally) to allow them to electronically comment on, correct, and markup the same, and
• to be able to ask (and occasionally answer, when I can help) questions about those topics here, on-wiki

I've read maybe two-hours worth of material about this so far, via the web, and our own articles, too, of course, and have naturally looked in the archives here. But I was hoping folks here could help me start out on the right foot by anwering a few probably naive questions, as well:

1. I like the idea of being able to generate pdf files easily, or better still(?), having a setup that uses pdf as a native file format for whatever I create using Tex, and I presume that means using the pdfTex extension. If this is correct, is there any LaTex/pdfTex editor that's free, relatively "standard"/ubiquitous (easy cross-platform availability), and that can edit pdf files directly?
2. About how much time will I need to reach a point point of minimal/reasonable proficiency? A point at which I can focus more on content, on writing math/logic documents, than on learning LaTex, that is?
3. I'd like to be able to use Russell & Whitehead's Principia Mathematica notation easily, if possible, and yes, I know it's been largely superseded in modern practice. ;-)
4. I'm using Ubuntu GNU/Debian/Linux, in case that matters.

All observations and suggestions will be most welcome. Many thanks,  – OhioStandard (talk) 16:04, 5 November 2010 (UTC)

I think it's difficult to give a general answer to this. In my case I wanted to write a mathematical paper, decided TeX and LaTeX would be the best way to do so, so downloaded the free TeXShop, bookmarked some documentation and started writing. I had a clear idea of the mathematics I wanted to write, it was just a case of finding the correct way to do it. As I did this on a paragraph by paragraph and equation by equation basis I slowly taught myself TeX. More recently I went through a similar process learning how to edit WP formulas, at the same time as learning Mediawiki syntax. Here my reference was WP itself and its help pages. In each case for me all I needed was an idea of what I wanted to do, access to documentation and examples, and a way to try out my ideas.

I notice from TeXShop there's a Comparison of TeX editors where you should be able to find a free editor. I don't know if you'll find one able to edit PDF files: PDF is designed for viewing only. Fast preview perhaps using PDF might be the best you can do.--JohnBlackburne^words_deeds 17:16, 5 November 2010 (UTC)

I'd suggest that a better place to look for answers to your questions might be http://tex.stackexchange.com/. --Qwfp (talk) 17:39, 5 November 2010 (UTC)

You seem to want general/open-ended answers. Any plain text editor will do for a LaTeX editor, since the point is to have everything in ASCII. I don't know about specific editors for Linux, sorry, other than the usual standard text editors. I have used one called TeXworks on Windows which I've liked, and it's apparently cross-platform. PDF files are generated from LaTeX source, for instance with the pdflatex command available in some/most Linux distros. To directly edit a PDF file, you would need (I believe) to edit postscript code, which isn't at all the same thing as editing LaTeX code (postscript isn't really meant to be hand-edited, anyway). A PDF file is to LaTeX as a compiled binary is to C++ source code--the compilation process isn't really reversible.

I've never read Principia myself, but a glance at this page suggests LaTeX would have no trouble at all typesetting it.

For me, it didn't take long to be minimally proficient. As a brief example, "\prod_{i=1}^{N^2} \int_{R_i}\Psi\,dA" renders as

$\prod _{i=1}^{N^{2}}\int _{R_{i}}\Psi \,dA$

If you can pattern match what most of that is doing, you can do a surprisingly large amount in LaTeX right now if given a few examples to work from. Depending on your computer proficiency, a good afternoon working with it should get you started. After figuring out how to make your system compile your source, I'd find a math paper online in TeX format and just try to write something up working from it as an example.

Personally, I hand write most of my math. I just find it much more freeing. Then again, I've heard that writing in LaTeX can become quite natural. 67.158.43.41 (talk) 17:53, 5 November 2010 (UTC)

Can we draw every mathematical concept?

In the case of simple concepts, it is evident that we can. Two segments on the same line are a sum. Two segments on a right angle are the equivalent of a multiplication. But, how about more complex concepts? Quest09 (talk) 17:40, 5 November 2010 (UTC)

If you want to really blow your mind, imagine that you write, in your programming language of choice (say C++), a programming environment, call it Crayon, to compile x86 code form a TOTALLY VISUAL programming paradigm. Now you draw in Crayon, and get x86 code. But Crayon is really still C++.

So imagine that you proceed to use Crayon to draw the EXACT SAME THING you had wrote in C++ to produce your current environment. Compile, and VOILA: you are now running Crayon, written in Crayon. Now you use Crayon -- written in Crayon -- to sketch out a rudimentary version of an operating system. It will take you years, but when you're done sketching it and compiling it, you can burn it to a CD-ROM.

Then you take it to a fresh computer, you put that CD-ROM in, you boot an Operating system not written in any programming language but sketched in Crayon, and you start up a copy of Crayon. YOUR WHOLE COMPUTING ENVIRONMENT WAS MADE WITHOUT A SINGLE LINE OF CODE! Without a single programming keyword. Without a single +, =, *, opening or closing brace, or any other symbol. It was all purely sketched out visually.

Well, what you have now, is what I imagine the Greeks would be running these days if it weren't for the Peloponnesian War. 84.153.205.142 (talk) 17:56, 5 November 2010 (UTC)