1.1) Define  . We are asked whether
. We are asked whether  . Observe that since
. Observe that since  is not a subset of
is not a subset of  it cannot possibly be a subgroup of
it cannot possibly be a subgroup of  . However, if what is meant is "Is
. However, if what is meant is "Is  a subgroup of
a subgroup of  ," then the answer is yes, because it
," then the answer is yes, because it
- a) contains the identity
 ,
,
- b) is closed under multiplication:
 , and
, and
- C) contains inverses:
 .
.
1.2) We are asked if  is cyclic. Again, since
is cyclic. Again, since  is not a subset of
is not a subset of  , it cannot possibly be a cyclic subgroup of
, it cannot possibly be a cyclic subgroup of  . If what is meant is "Is
. If what is meant is "Is  a cyclic subgroup of
a cyclic subgroup of  ," the answer is still no. Suppose
," the answer is still no. Suppose  is not cyclic. Observe that the map
is not cyclic. Observe that the map  defined
defined  is an isomorphism, since it is necessarily bijective, and satisfies
is an isomorphism, since it is necessarily bijective, and satisfies  . Then
. Then  is not cyclic.
is not cyclic.
1.5) Observe that for all  , we have
, we have  . If
. If  is commutative, then this is just
is commutative, then this is just  . So,
. So,  commutative
commutative  .
.
Now suppose  . Then
. Then  . In particular,
. In particular,  and
and  for all
for all  . But this is just
. But this is just
 and
and  .
.
or
 .
.
Hence G is commutative, so  is commutative.
is commutative.
Therefore,  is commutative.
is commutative.
1.3, 1.4) By 1.5, these are necessarily false.
2.1) We are asked if every nontrivial group  contains a non-trivial proper subgroup
contains a non-trivial proper subgroup  . This is false. Consider the group
. This is false. Consider the group  . By Lagrange's theorem, a subgroup of this must have order either 1 or 3. But this means a subgroup must be either trivial, or the group itself, ie, not proper.
. By Lagrange's theorem, a subgroup of this must have order either 1 or 3. But this means a subgroup must be either trivial, or the group itself, ie, not proper.
2.2) We are asked if every nontrivial group  contains a normal nontrivial proper subgroup
contains a normal nontrivial proper subgroup  . This is false. See problem 1.
. This is false. See problem 1.
2.3) We are asked if every group  can be embedded in a larger group
can be embedded in a larger group  such that
such that  is normal in
is normal in  . This is true. Let
. This is true. Let  be any group with operation
be any group with operation  and identity
and identity  , and define the set
, and define the set  and the operation
and the operation  as
as

Observe that  is necessarily closed under
is necessarily closed under  , since
, since  is closed under
is closed under  and
and  is closed under
is closed under  .
.
Furthermore, since both these operations are associative,  is as well.
is as well.
We certainly have an identity, namely  : observe
: observe  , and inverses defined
, and inverses defined  :
:
 .
.
Hence,  is a group.
is a group.
Define the map  as
as  . Observe that
. Observe that
 ,
,
and so  is a homomorphism. Now suppose
is a homomorphism. Now suppose  . Then
. Then  , and so
, and so  is an injective homomorphism, with
is an injective homomorphism, with  and
and  .
.
Let  be any element. Observe that for any element
be any element. Observe that for any element  , we have
, we have
 .
.
Hence,  .
.
3) Let  be commutative rings with identity,
be commutative rings with identity,  a ring homomorphism, and
a ring homomorphism, and  an ideal in
an ideal in  . We aim to show there is a unique ring homomorphism
. We aim to show there is a unique ring homomorphism  such that
such that  , where
, where  is the canonical homomorphism
is the canonical homomorphism  defined
defined  .
.
We construct the commutative diagram
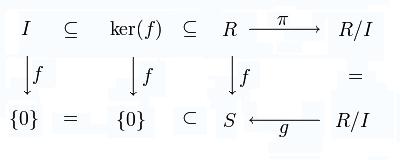
This suggests the definition  . Note that if this is a well-defined homomorphism, then we automatically have
. Note that if this is a well-defined homomorphism, then we automatically have  .
.
Let  be any element. We can write this as
be any element. We can write this as  . Then
. Then  , and so this is a well-defined function. Furthermore, we have
, and so this is a well-defined function. Furthermore, we have
 ,
,
since  is a homomorphism, and
is a homomorphism, and
 ,
,
again, since  is a homomorphism. Therefore,
is a homomorphism. Therefore,  is a well-defined ring homomorphism.
is a well-defined ring homomorphism.
Now suppose  is any ring homomorphism and that
is any ring homomorphism and that  satisfies
satisfies  .
.
Then  . So such
. So such  is unique.
is unique.
4) We are asked to determine which rings are isomorphic:
![{\displaystyle A=\mathbb {C} [x]/(x^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/9079215c72be74b2af9efe2663d64b57309b405f) ,
,
![{\displaystyle B=\mathbb {C} [x]/((x-1)^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/362c0d3ca28a5e448285aeff89593fba1f95f934) ,
,
![{\displaystyle C=\mathbb {C} [x]/(x^{3})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/f3519c0d308dbb0a85ef6995aca21ce483c8c527) ,
,
![{\displaystyle D=\mathbb {C} [x]/(x^{2}+1)\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/0de49b69bad46c4eb5d4fbc172a309625cc5287e) ,
,
 .
.
For  and
and  , consider the map
, consider the map ![{\displaystyle \phi :\mathbb {C} [x]\to \mathbb {C} [x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/3db50d2442454599e5936e3c3e894d5ea91bfca0) defined
defined  .
.
This map is clearly an automorphism of ![{\displaystyle \mathbb {C} [x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/cfe6be6ca3a9111ba4947c44aa6d32e4012ea0d3) sending
sending  . Let
. Let  be the canonical homomorphism
be the canonical homomorphism ![{\displaystyle \pi :\mathbb {C} [x]\to \mathbb {C} [x]/((x-1)^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/57ba9107de7c04efecc103df56a35e6b77df5c53) .
.
Observe that  . Since
. Since ![{\displaystyle \pi \circ f:\mathbb {C} [x]\to \mathbb {C} [x]/((x-1)^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/fcfd4c9ca4b84f302b2966424ecb62cc7f0a6e72) is a homomorphism with kernel
is a homomorphism with kernel  , we must have
, we must have
![{\displaystyle \mathbb {C} [x]/(x^{2})\cong \mathbb {C} [x]/((x-1)^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/8a6313efa8f53db0905039fb9b8b47b7c08c648b) .
.
So  .
.
Observe  , considered as a vector space over
, considered as a vector space over  , has dimension 2, while
, has dimension 2, while  has dimension 3 as a vector space. Since
has dimension 3 as a vector space. Since  as vector spaces, they cannot be isomorphic as rings:
as vector spaces, they cannot be isomorphic as rings:  .
.
For  and
and  , observe that by the division algorithm, any polynomial
, observe that by the division algorithm, any polynomial ![{\displaystyle p(x)\in \mathbb {C} [x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/1d2dc5b78b0beaa8a458eeaef6076b7225cf781b) can be written
can be written  where
where  , and so
, and so  is isomorphic to
is isomorphic to  . Hence,
. Hence,  .
.
We show that ![{\displaystyle A=\mathbb {C} [x]/(x^{2})=\left\{{a+bx:a,b\in \mathbb {C} }\right\}\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/16dbdb06401996d1a98b359dc82de09ab68d55f3) is not ring isomorphic to
is not ring isomorphic to  using a proof by contradiction. Suppose these two rings are isomorphic. Then there is a ring homomorphism
using a proof by contradiction. Suppose these two rings are isomorphic. Then there is a ring homomorphism ![{\displaystyle \phi :\mathbb {C} [x]\to \mathbb {C} \times \mathbb {C} \ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/18d37f49ed8a0c65136a6c25bf5fd71d860fb464) such that
such that  .
.
Observe that since  is a homomorphism, we must also have
is a homomorphism, we must also have
 .
.
Therefore, either  or
or  is a zero divisor. Since
is a zero divisor. Since  , the first possibility contradicts our requirement that
, the first possibility contradicts our requirement that  .
.
The only zero divisors in  are of the forms
are of the forms  , so we must have
, so we must have  for some
for some  .
.
But we may also observe that  which must also be a zero divisor. Since zero divisors in
which must also be a zero divisor. Since zero divisors in  can satisfy
can satisfy  , which is not a zero divisor, we can say that either
, which is not a zero divisor, we can say that either  or
or  . Without loss of generality, we can assume the first case is true.
. Without loss of generality, we can assume the first case is true.
Since  , and since
, and since  is a homomorphism, observe that
is a homomorphism, observe that
 .
.
Since  , we must have
, we must have  as zero divisors in
as zero divisors in  . But
. But  has no zero divisors, and so no such homomorphism
has no zero divisors, and so no such homomorphism  exists. Hence,
exists. Hence,  .
.
Observe that the ring ![{\displaystyle C=\mathbb {C} [x]/(x^{3})=\left\{{ax^{2}+bx+c:a,b,c\in \mathbb {C} }\right\}\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/04bb137640f0abc9cb93e9bd9e7bc47c36d4d337) has dimension 3 as a vector space. Since
has dimension 3 as a vector space. Since  has dimension 2 as a vector space, they cannot be isomorphic as vector spaces, and so they cannot be isomorphic as rings:
has dimension 2 as a vector space, they cannot be isomorphic as vector spaces, and so they cannot be isomorphic as rings:  .
.
Since we have  , we must have
, we must have  . Since
. Since  , we must have
, we must have  . We have also shown
. We have also shown  . We can summarize these results in a table:
. We can summarize these results in a table:
| •
|
A
|
B
|
C
|
D
|
E
|
| A
|
 |
 |
 |
 |

|
| B
|
 |
 |
 |
 |

|
| C
|
 |
 |
 |
 |

|
| D
|
 |
 |
 |
 |

|
| E
|
 |
 |
 |
 |

|
5) With  defined as in problem 4, we are asked to find all pairs of isomorphic vector spaces. From (4), and the fact that if two rings are isomorphic, they are isomorphic as vector spaces, we have
defined as in problem 4, we are asked to find all pairs of isomorphic vector spaces. From (4), and the fact that if two rings are isomorphic, they are isomorphic as vector spaces, we have
 .
.
Define the map  as
as  . Observe that this map is necessarily bijective, and that
. Observe that this map is necessarily bijective, and that
 ,
,
and so  .
.
As in question 4, we note that  , and so as vector spaces,
, and so as vector spaces,  . Since
. Since  , we must have
, we must have  and
and  .
.
We summarize these results in a table:
| •
|
A
|
B
|
C
|
D
|
E
|
| A
|
 |
 |
 |
 |

|
| B
|
 |
 |
 |
 |

|
| C
|
 |
 |
 |
 |

|
| D
|
 |
 |
 |
 |

|
| E
|
 |
 |
 |
 |

|
6.1) Let  be a finite field of characteristic
be a finite field of characteristic  and define the map
and define the map  as
as  . We are given that this is a homomorphism; we aim to show that this is an automorphism.
. We are given that this is a homomorphism; we aim to show that this is an automorphism.
To show that  is an automorphism, it suffices to show that it is a bijection from
is an automorphism, it suffices to show that it is a bijection from  .
.
- Injection:
Suppose  and
and  . We aim to show that
. We aim to show that  , meaning
, meaning  is an injection. Our assumption
is an injection. Our assumption  means
means  . By multiplying both sides by
. By multiplying both sides by  , we have
, we have  , which we can rewrite as
, which we can rewrite as  . Raising both sides to the
. Raising both sides to the  power, we have
power, we have  , but since
, but since  , this is just
, this is just  . Since
. Since  is a multiplicative inverse of both
is a multiplicative inverse of both  , and since multiplicative inverses are unique, we must have
, and since multiplicative inverses are unique, we must have  . Hence
. Hence  is an injection.
is an injection.
- Surjection:
Let  be any element. We aim to show
be any element. We aim to show  . This would demonstrate
. This would demonstrate  is a surjection.
is a surjection.
Since  is an injection, we can be sure that
is an injection, we can be sure that  .
.
This means that  , because
, because  , which we know to be false. But then since
, which we know to be false. But then since  is finite,
is finite,  . Hence
. Hence  is a surjection.
is a surjection.
6.2) Note that the surjective proof in 6.1 fails if  , because then
, because then  . We can find a specific counterexample in
. We can find a specific counterexample in  , the field of fractions of
, the field of fractions of ![{\displaystyle F[x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/633ae60c7db351b0bb0433e84aadb1af8d0a26ec) , where
, where  is a finite field of characteristic
is a finite field of characteristic  .
.
Observe that since  is a field,
is a field, ![{\displaystyle F[x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/633ae60c7db351b0bb0433e84aadb1af8d0a26ec) is an integral domain, and so by Theorem 15, pg 261 of Dummit and Foote,
is an integral domain, and so by Theorem 15, pg 261 of Dummit and Foote,  is a field.
is a field.
Further observe that  , so
, so  .
.
Observe that if  is an irreducible polynomial in
is an irreducible polynomial in ![{\displaystyle F[x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/633ae60c7db351b0bb0433e84aadb1af8d0a26ec) , then the statement "
, then the statement " " is equivalent to saying
" is equivalent to saying  ," since
," since  in lowest terms implies
in lowest terms implies  is in lowest terms. Since we have assumed
is in lowest terms. Since we have assumed  is irreducible, this is a contradiction, and hence
is irreducible, this is a contradiction, and hence  cannot have a pre-image in
cannot have a pre-image in  .
.



























































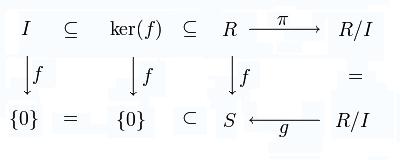












![{\displaystyle A=\mathbb {C} [x]/(x^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/9079215c72be74b2af9efe2663d64b57309b405f)
![{\displaystyle B=\mathbb {C} [x]/((x-1)^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/362c0d3ca28a5e448285aeff89593fba1f95f934)
![{\displaystyle C=\mathbb {C} [x]/(x^{3})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/f3519c0d308dbb0a85ef6995aca21ce483c8c527)
![{\displaystyle D=\mathbb {C} [x]/(x^{2}+1)\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/0de49b69bad46c4eb5d4fbc172a309625cc5287e)



![{\displaystyle \phi :\mathbb {C} [x]\to \mathbb {C} [x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/3db50d2442454599e5936e3c3e894d5ea91bfca0)

![{\displaystyle \mathbb {C} [x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/cfe6be6ca3a9111ba4947c44aa6d32e4012ea0d3)

![{\displaystyle \pi :\mathbb {C} [x]\to \mathbb {C} [x]/((x-1)^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/57ba9107de7c04efecc103df56a35e6b77df5c53)

![{\displaystyle \pi \circ f:\mathbb {C} [x]\to \mathbb {C} [x]/((x-1)^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/fcfd4c9ca4b84f302b2966424ecb62cc7f0a6e72)

![{\displaystyle \mathbb {C} [x]/(x^{2})\cong \mathbb {C} [x]/((x-1)^{2})\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/8a6313efa8f53db0905039fb9b8b47b7c08c648b)






![{\displaystyle p(x)\in \mathbb {C} [x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/1d2dc5b78b0beaa8a458eeaef6076b7225cf781b)




![{\displaystyle A=\mathbb {C} [x]/(x^{2})=\left\{{a+bx:a,b\in \mathbb {C} }\right\}\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/16dbdb06401996d1a98b359dc82de09ab68d55f3)
![{\displaystyle \phi :\mathbb {C} [x]\to \mathbb {C} \times \mathbb {C} \ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/18d37f49ed8a0c65136a6c25bf5fd71d860fb464)


















![{\displaystyle C=\mathbb {C} [x]/(x^{3})=\left\{{ax^{2}+bx+c:a,b,c\in \mathbb {C} }\right\}\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/04bb137640f0abc9cb93e9bd9e7bc47c36d4d337)















































![{\displaystyle F[x]\ }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/633ae60c7db351b0bb0433e84aadb1af8d0a26ec)






