Rectified 5-cubes

Rectified 5-cube
Orthogonal projection Projected in B5 Coxeter plane
Type	uniform polyteron
Schläfli symbol	t1{4,3,3,3}
Coxeter-Dynkin diagrams
4-faces	42
Cells	200
Faces	400
Edges	320
Vertices	80
Vertex figure	tetrahedral prism
Petrie polygon	Decagon
Coxeter groups	C5, [3,3,3,4]
Properties	convex

In five-dimensional geometry, a rectified 5-cube is a uniform 5-polytope, constructed as a rectification of the regular 5-cube.

Alternate names

• Rectified penteract (acronym: rin) (Jonathan Bowers)

Construction

The rectified 5-cube may be constructed from the 5-cube by truncating its vertices at the midpoints of its edges.

The Cartesian coordinates of the vertices of the rectified 5-cube with edge length ${\sqrt {2}}$ is given by all permutations of:

$(0,\ \pm 1,\ \pm 1,\ \pm 1,\ \pm 1)$

Images

orthographic projections

Coxeter plane	B5	B4 / D5	B3 / D4 / A2
Graph
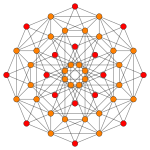
Dihedral symmetry	[10]	[8]	[6]
Coxeter plane	B2	A3
Graph
Dihedral symmetry	[4]	[4]

Related polytopes

This polytope is one of 31 uniform polytera generated from the regular 5-cube or 5-orthoplex.

B5 polytopes
β5	t1β5	t2γ5	t1γ5	γ5	t0,1β5	t0,2β5	t1,2β5
t0,3β5	t1,3γ5	t1,2γ5	t0,4γ5	t0,3γ5	t0,2γ5	t0,1γ5	t0,1,2β5
t0,1,3β5	t0,2,3β5	t1,2,3γ5	t0,1,4β5	t0,2,4γ5	t0,2,3γ5	t0,1,4γ5	t0,1,3γ5
t0,1,2γ5	t0,1,2,3β5	t0,1,2,4β5	t0,1,3,4γ5	t0,1,2,4γ5	t0,1,2,3γ5	t0,1,2,3,4γ5

See also

• Other 5-polytopes:
  • 5-simplex - {3,3,3,3}
  • 5-cube (penteract) - {4,3,3,3}
  • 5-demicube (demipenteract) - {3^1,2,1}

External links

• Weisstein, Eric W. "Hypercube". MathWorld.
• Olshevsky, George. "Measure polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Polytopes of Various Dimensions
• Multi-dimensional Glossary
• Klitzing, Richard. "5D uniform polytopes (polytera) o3x3o3o4o - rin".