AVL tree: Difference between revisions
No edit summary |
|||
| Line 84: | Line 84: | ||
{{More footnotes|date=May 2010}} |
{{More footnotes|date=May 2010}} |
||
* [[Donald Knuth]]. ''The Art of Computer Programming'', Volume 3: ''Sorting and Searching'', Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 458–475 of section 6.2.3: Balanced Trees. |
* [[Donald Knuth]]. ''The Art of Computer Programming'', Volume 3: ''Sorting and Searching'', Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 458–475 of section 6.2.3: Balanced Trees. |
||
==See also== |
|||
*[[tree data structure|Trees]] |
|||
*[[Tree rotation]] |
|||
*[[Splay tree]] |
|||
*[[B-tree]] |
|||
*[[T-tree]] |
|||
*[[List of data structures]] |
|||
==External links== |
==External links== |
||
Revision as of 20:09, 1 April 2011
This article needs additional citations for verification. (October 2007) |
| AVL tree | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | tree | |||||||||||||||||||||||
| Invented | 1962 | |||||||||||||||||||||||
| Invented by | G.M. Adelson-Velskii and E.M. Landis | |||||||||||||||||||||||
| ||||||||||||||||||||||||
In computer science, an AVL tree is a self-balancing binary search tree, and it was the first such data structure to be invented.[1] In an AVL tree, the heights of the two child subtrees of any node differ by at most one. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
The AVL tree is named after its two Soviet inventors, G.M. Adelson-Velskii and E.M. Landis, who published it in their 1962 paper "An algorithm for the organization of information."[2]
The balance factor of a node is the height of its left subtree minus the height of its right subtree (sometimes opposite) and a node with balance factor 1, 0, or −1 is considered balanced. A node with any other balance factor is considered unbalanced and requires rebalancing the tree. The balance factor is either stored directly at each node or computed from the heights of the subtrees.
AVL trees are often compared with red-black trees because they support the same set of operations and because red-black trees also take O(log n) time for the basic operations. Because AVL trees are more rigidly balanced, they are faster than red-black trees for lookup intensive applications.[3] However, red-black trees have faster insertion and removal times.
Operations
The basic operations of an AVL tree involve carrying out the same actions as would be carried out on an unbalanced binary search tree, but modifications are preceded or followed by one or more operations called tree rotations, which help to restore the height balance of the subtrees.
Lookup
Lookup in an AVL tree is performed exactly as in an unbalanced binary search tree. Because of the height-balancing of the tree, a lookup takes O(log n) time. No special actions need to be taken, and the tree's structure is not modified by lookups. (This is in contrast to splay tree lookups, which do modify their tree's structure.)
If each node additionally records the size of its subtree (including itself and its descendants), then the nodes can be retrieved by index in O(log n) time as well.
Once a node has been found in a balanced tree, the next or previous nodes can be explored in amortized constant time. A few cases require traversing up to 2×log(n) links. However exploring all n nodes in the tree in this manner would use each link exactly twice, and there are n−1 links, so the amortized cost is 2×(n−1)/n, approximately 2.
Insertion
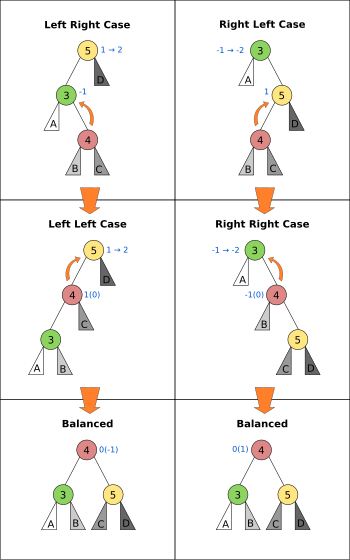
After inserting a node, it is necessary to check each of the node's ancestors for consistency with the rules of AVL (in what order? bottom-up, right?). For each node checked, if the balance factor remains −1, 0, or +1 then no rotations are necessary. However, if the balance factor becomes ±2 then the subtree rooted at this node is unbalanced. If insertions are performed serially, after each insertion, at most one tree rotation is needed to restore the entire tree to the rules of AVL.
There are four cases which need to be considered, of which two are symmetric to the other two. Let P be the root of the unbalanced subtree. Let R be the right child of P. Let L be the left child of P.
Right-Right case and Right-Left case: If the balance factor of P is −2, then the right subtree outweighs the left subtree of the given node, and the balance factor of the right child (R) must be checked. If the balance factor of R is < 0, a left rotation is needed with P as the root. If the balance factor of R is +1, a double left rotation (with respect to P) is needed. The first rotation is a right rotation with R as the root. The second is a left rotation with P as the root.
Left-Left case and Left-Right case: If the balance factor of P is +2, then the left subtree outweighs the right subtree of the given node, and the balance factor of the left child (L) must be checked. If the balance factor of L is > 0, a right rotation is needed with P as the root. If the balance factor of L is −1, a double right rotation (with respect to P) is needed. The first rotation is a left rotation with L as the root. The second is a right rotation with P as the root.
Algorithms for all the above four cases can be found here.
Deletion
If the node is a leaf or has only one child, remove it. Otherwise, replace it with either the largest in its left subtree (inorder predecessor) or the smallest in its right subtree (inorder successor), and remove that node. The node that was found as a replacement has at most one subtree. After deletion, retrace the path back up the tree (parent of the replacement) to the root, adjusting the balance factors as needed.
As with all binary trees, a node's in-order successor is the left-most child of its right subtree, and a node's in-order predecessor is the right-most child of its left subtree. In either case, this node will have zero or one children. Delete it according to one of the two simpler cases above.
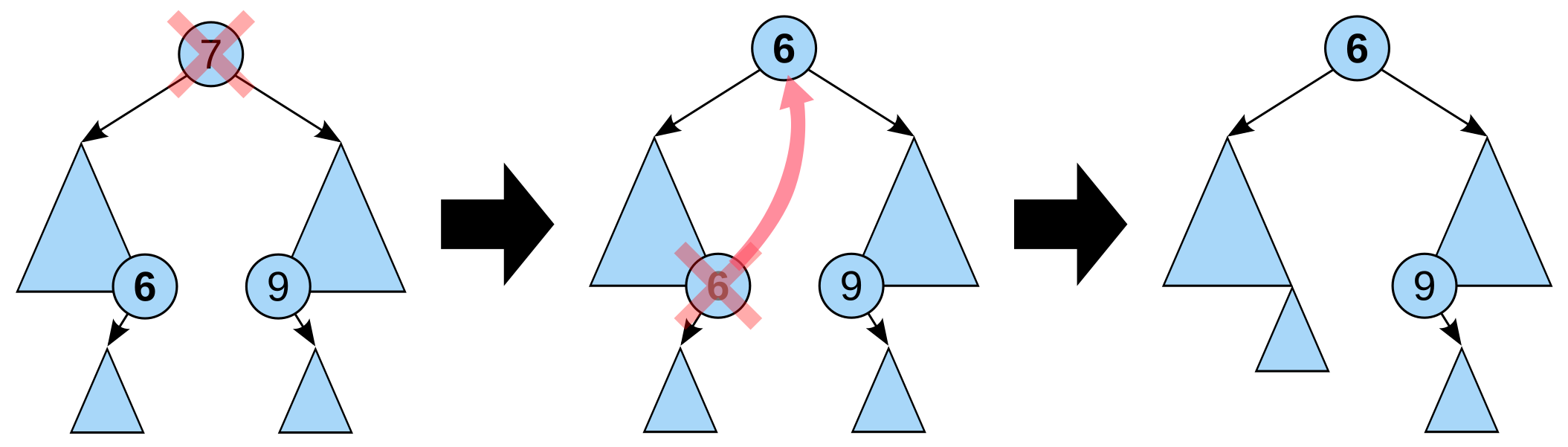
In addition to the balancing described above for insertions, if the balance factor for the tree is 2 and that of the left subtree is 0, a right rotation must be performed on P. The mirror of this case is also necessary.
The retracing can stop if the balance factor becomes −1 or +1 indicating that the height of that subtree has remained unchanged. If the balance factor becomes 0 then the height of the subtree has decreased by one and the retracing needs to continue. If the balance factor becomes −2 or +2 then the subtree is unbalanced and needs to be rotated to fix it. If the rotation leaves the subtree's balance factor at 0 then the retracing towards the root must continue since the height of this subtree has decreased by one. This is in contrast to an insertion where a rotation resulting in a balance factor of 0 indicated that the subtree's height has remained unchanged.
The time required is O(log n) for lookup, plus a maximum of O(log n) rotations on the way back to the root, so the operation can be completed in O(log n) time.
Comparison to other structures
Both AVL trees and red-black trees are self-balancing binary search trees, so they are very similar mathematically. The operations to balance the trees are different, but both occur in O(log n) time. The real difference between the two is the limiting height. For a tree of size :
- An AVL tree's height is strictly less than:[4]
where is the golden ratio.
- A red-black tree's height is at most [5]
AVL trees are more rigidly balanced than red-black trees, leading to slower insertion and removal but faster retrieval.
References
- ^ Robert Sedgewick, Algorithms, Addison-Wesley, 1983, ISBN 0-201-06672-6, page 199, chapter 15: Balanced Trees.
- ^ Adelson-Velskii, G. (1962). "An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences. 146: 263–266.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) Template:Ru icon English translation by Myron J. Ricci in Soviet Math. Doklady, 3:1259–1263, 1962. - ^ Pfaff, Ben (2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University.
{{cite web}}: Unknown parameter|month=ignored (help) - ^ Burkhard, Walt (Spring 2010). "AVL Dictionary Data Type Implementation". Advanced Data Structures (PDF). La Jolla: A.S. Soft Reserves, UC San Diego. p. 99.
{{cite book}}: External link in|publisher= - ^ Proof of asymptotic bounds
Further reading
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (May 2010) |
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 458–475 of section 6.2.3: Balanced Trees.
See also
External links
- Description from the Dictionary of Algorithms and Data Structures
- C++ Implementation
- Python Implementation
- Single C header file by Ian Piumarta
- AVL Tree Demonstration
- AVL Tree in examples
- AVL tree applet
- Fast and efficient implementation of AVL Trees
- PowerPoint Teaching Slides for the insertion and deletion algorithms of AVL Trees
- Animated AVL Tree




