Truncated triakis tetrahedron: Difference between revisions
→External links: number 23 (the linked page has change) |
KirbyRider (talk | contribs) No edit summary |
||
| Line 11: | Line 11: | ||
|- |
|- |
||
|bgcolor=#e7dcc3|Vertices||28 |
|bgcolor=#e7dcc3|Vertices||28 |
||
|- |
|||
|bgcolor=#e7dcc3|Dual|[[Hexakis truncated tetrahedron]] |
|||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Vertex configuration]]||4 (5.5.5)<BR>24 (5.5.6) |
|bgcolor=#e7dcc3|[[Vertex configuration]]||4 (5.5.5)<BR>24 (5.5.6) |
||
| Line 22: | Line 24: | ||
A topologically similar [[equilateral]] polyhedron can be constructed by using 12 [[Regular polygon|regular]] pentagons with 4 [[equilateral]] but nonplanar hexagons, each vertex with [[internal angle]]s alternating between 108 and 132 degrees. |
A topologically similar [[equilateral]] polyhedron can be constructed by using 12 [[Regular polygon|regular]] pentagons with 4 [[equilateral]] but nonplanar hexagons, each vertex with [[internal angle]]s alternating between 108 and 132 degrees. |
||
==Full Truncation== |
|||
A Triakis Tetrahedron can be fully truncated, not giving out this. The Full truncation is a special type of icosahedron, rather than a hexadecahedron. Another alternate truncation, or the "Low order truncation", will give out what looks like a [[Tetrahedron]] with each face raised by a low [[Pyramidal frustum|Triangular frustum]]. The dual to that truncation will be the "Triakis Truncated Tetrahedron". However, the full truncation is dual to a ''Trihexakis truncated tetrahedron''. |
|||
[[Image:Truncated triakis tetrahedron.png|240px|The common truncation]] [[File:StellaTruncTriakisTetra.png|120px|The Full Truncation]] |
|||
== See also == |
== See also == |
||
* [[Near-miss Johnson solid]] |
* [[Near-miss Johnson solid]] |
||
Revision as of 19:05, 25 May 2011
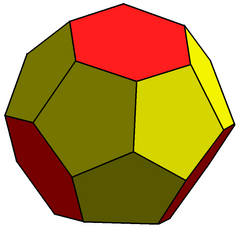
| Truncated triakis tetrahedron | |
|---|---|
| |
| Type | Conway polyhedron |
| Faces | 4 hexagons 12 pentagons |
| Edges | 42 |
| Vertices | 28 |
| Dual|Hexakis truncated tetrahedron | |
| Vertex configuration | 4 (5.5.5) 24 (5.5.6) |
| Symmetry group | Td |
| Properties | convex |
The truncated triakis tetrahedron is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a tetrahedral arrangement, with 4 hexagons in the gaps. It is constructed from taking a triakis tetrahedron by truncating the order-6 vertices. This creates 4 regular hexagon faces, and leaves 12 irregular pentagons.
A topologically similar equilateral polyhedron can be constructed by using 12 regular pentagons with 4 equilateral but nonplanar hexagons, each vertex with internal angles alternating between 108 and 132 degrees.
Full Truncation
A Triakis Tetrahedron can be fully truncated, not giving out this. The Full truncation is a special type of icosahedron, rather than a hexadecahedron. Another alternate truncation, or the "Low order truncation", will give out what looks like a Tetrahedron with each face raised by a low Triangular frustum. The dual to that truncation will be the "Triakis Truncated Tetrahedron". However, the full truncation is dual to a Trihexakis truncated tetrahedron.