Pareto distribution

Pareto

Probability density function Pareto probability density functions for various α  with xm = 1. The horizontal axis is the x  parameter. As α → ∞ the distribution approaches δ(x − xm) where δ is the Dirac delta function.
Cumulative distribution function Pareto cumulative distribution functions for various α  with xm = 1. The horizontal axis is the x  parameter.
Parameters	$x_{\mathrm {m} }>0\,$ scale (real) $\alpha >0\,$ shape (real)
Support	$x\in [x_{\mathrm {m} },+\infty )\!$
PDF	${\frac {\alpha \,x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}{\text{ for }}x\geq x_{m}\!$
CDF	$1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }{\text{ for }}x\geq x_{m}\!$
Mean	${\frac {\alpha \,x_{\mathrm {m} }}{\alpha -1}}{\text{ for }}\alpha >1\,$
Median	$x_{\mathrm {m} }{\sqrt[{\alpha }]{2}}$
Mode	$x_{\mathrm {m} }\,$
Variance	${\frac {x_{\mathrm {m} }^{2}\alpha }{(\alpha -1)^{2}(\alpha -2)}}{\text{ for }}\alpha >2\,$
Skewness	${\frac {2(1+\alpha )}{\alpha -3}}\,{\sqrt {\frac {\alpha -2}{\alpha }}}{\text{ for }}\alpha >3\,$
Excess kurtosis	${\frac {6(\alpha ^{3}+\alpha ^{2}-6\alpha -2)}{\alpha (\alpha -3)(\alpha -4)}}{\text{ for }}\alpha >4\,$
Entropy	$\ln \left({\frac {x_{\mathrm {m} }}{\alpha }}\right)+{\frac {1}{\alpha }}+1\!$
MGF	$\alpha (-x_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-x_{\mathrm {m} }t){\text{ for }}t<0\,$
CF	$\alpha (-ix_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t)\,$
Fisher information	${\begin{pmatrix}{\frac {\alpha }{x_{m}^{2}}}&-{\frac {1}{x_{m}}}\\-{\frac {1}{x_{m}}}&{\frac {1}{\alpha ^{2}}}\end{pmatrix}}$

The Pareto distribution, named after the Italian economist Vilfredo Pareto, is a power law probability distribution that coincides with social, scientific, geophysical, actuarial, and many other types of observable phenomena. Outside the field of economics it is sometimes referred to as the Bradford distribution.

Properties

Definition

If X is a random variable with a Pareto (Type I) distribution, then the probability that X is greater than some number x is given by

$\Pr(X>x)={\begin{cases}\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&{\text{for }}x\geq x_{\mathrm {m} },\\1&{\text{for }}x<x_{\mathrm {m} }.\end{cases}}$

where x_m is the (necessarily positive) minimum possible value of X, and α is a positive parameter. The family of Pareto distributions is parameterized by two quantities, x_m and α. When this distribution is used to model the distribution of wealth, then the parameter α is called the Pareto index.

It follows from the above that the cumulative distribution function of a Pareto random variable with parameters α and x_m is

$F_{X}(x)={\begin{cases}1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&{\text{for }}x\geq x_{\mathrm {m} },\\0&{\text{for }}x<x_{\mathrm {m} }.\end{cases}}$

Graphical representation

When plotted on linear axes, the distribution assumes the familiar J-shaped curve which approaches each of the orthogonal axes asymptotically. All segments of the curve are self-similar (subject to appropriate scaling factors).

When plotted on logarithmic scales (both axes logarithmic), the distribution is represented by a straight line.

Density function

It follows (by differentiation) that the probability density function is

$f_{X}(x)={\begin{cases}\alpha \,{\dfrac {x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}&{\text{for }}x>x_{\mathrm {m} },\\[12pt]0&{\text{for }}x<x_{\mathrm {m} }.\end{cases}}$

Moments and characteristic function

• The expected value of a random variable following a Pareto distribution with α > 1 is

$E(X)={\frac {\alpha x_{\mathrm {m} }}{\alpha -1}}\,$

(if α ≤ 1, the expected value does not exist).

• The variance is

$\mathrm {Var} (X)=\left({\frac {x_{\mathrm {m} }}{\alpha -1}}\right)^{2}{\frac {\alpha }{\alpha -2}}.$

(If α ≤ 2, the variance does not exist.)

• The raw moments are

$\mu _{n}'={\frac {\alpha x_{\mathrm {m} }^{n}}{\alpha -n}},\,$

but the nth moment exists only for n < α.

• The moment generating function is only defined for non-positive values t ≤ 0 as

$M\left(t,\alpha ,x_{\mathrm {m} }\right)=E(e^{tX})=\alpha (-x_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-x_{\mathrm {m} }t){\text{ and }}M\left(0,\alpha ,x_{\mathrm {m} }\right)=1.\,$

• The characteristic function is given by

$\varphi (t;\alpha ,x_{\mathrm {m} })=\alpha (-ix_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t),$

where Γ(a, x) is the incomplete gamma function.

Degenerate case

The Dirac delta function is a limiting case of the Pareto density:

$\lim _{\alpha \rightarrow \infty }f(x;\alpha ,x_{\mathrm {m} })=\delta (x-x_{\mathrm {m} }).\,$

Conditional distributions

The conditional probability distribution of a Pareto-distributed random variable, given the event that it is greater than or equal to a particular number x₁ exceeding x_m, is a Pareto distribution with the same Pareto index α but with minimum x₁ instead of x_m.

A characterization theorem

Suppose X_i, i = 1, 2, 3, ... are independent identically distributed random variables whose probability distribution is supported on the interval [x_m, ∞) for some x_m > 0. Suppose that for all n, the two random variables min{ X₁, ..., X_n } and (X₁ + ... + X_n)/min{ X₁, ..., X_n } are independent. Then the common distribution is a Pareto distribution.

Applications

Pareto originally used this distribution to describe the allocation of wealth among individuals since it seemed to show rather well the way that a larger portion of the wealth of any society is owned by a smaller percentage of the people in that society. He also used it to describe distribution of income. This idea is sometimes expressed more simply as the Pareto principle or the "80-20 rule" which says that 20% of the population controls 80% of the wealth. The probability density function (PDF) graph on the right shows that the "probability" or fraction of the population that owns a small amount of wealth per person is rather high, and then decreases steadily as wealth increases. This distribution is not limited to describing wealth or income, but to many situations in which an equilibrium is found in the distribution of the "small" to the "large". The following examples are sometimes seen as approximately Pareto-distributed:

• The sizes of human settlements (few cities, many hamlets/villages)
• File size distribution of Internet traffic which uses the TCP protocol (many smaller files, few larger ones)
• Hard disk drive error rates
• Clusters of Bose–Einstein condensate near absolute zero
• The values of oil reserves in oil fields (a few large fields, many small fields)
• The length distribution in jobs assigned supercomputers (a few large ones, many small ones)
• The standardized price returns on individual stocks

Fitted cumulative Pareto distribution to maximum one-day rainfalls using CumFreq

• Sizes of sand particles
• Sizes of meteorites
• Numbers of species per genus (There is subjectivity involved: The tendency to divide a genus into two or more increases with the number of species in it)
• Areas burnt in forest fires
• Severity of large casualty losses for certain lines of business such as general liability, commercial auto, and workers compensation.
• In hydrology the Pareto distribution is applied to extreme events such as annually maximum one-day rainfalls and river discharges. The blue picture illustrates an example of fitting the Pareto distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.

Relation to other distributions

Relation to the log-normal distribution

Note that the Pareto distribution and log-normal distribution are alternative distributions for describing the same types of quantities. One of the connections between the two is that they are both the distributions of the exponential of random variables distributed according to other common distributions, respectively the exponential distribution and normal distribution. (Both of these latter two distributions are "basic" in the sense that the logarithms of their density functions are linear and quadratic, respectively, functions of the observed values.)

Relation to the generalized Pareto distribution

The Pareto distribution is a special case of the generalized Pareto distribution, which is a family of distributions of similar form, but containing an extra parameter in such a way that the support of the distribution is either bounded below (at a variable point), or bounded both above and below (where both are variable). This family also contains both the unshifted and shifted exponential distributions.

Relation to the exponential distribution

The Pareto distribution is related to the exponential distribution as follows. If X is Pareto-distributed with minimum x_m and index α, then

$Y=\log \left({\frac {X}{x_{\mathrm {m} }}}\right).$

is exponentially distributed with intensity α. Equivalently, if Y is exponentially distributed with intensity α, then

$x_{\mathrm {m} }e^{Y}\,$

is Pareto-distributed with minimum x_m and index α.

This can be shown using the standard change of variable techniques:

$\Pr(Y<y)=\Pr \left(\log \left({\frac {X}{x_{\mathrm {m} }}}\right)<y\right)=\Pr(X<x_{\mathrm {m} }e^{y})=1-\left({\frac {x_{\mathrm {m} }}{x_{\mathrm {m} }e^{y}}}\right)^{\alpha }=1-\exp(-y\alpha ).$

The last expression is the cumulative distribution function of an exponential distribution with intensity α.

Relation to Zipf's law

Pareto distributions are continuous probability distributions. Zipf's law, also sometimes called the zeta distribution, may be thought of as a discrete counterpart of the Pareto distribution.

Relation to the "Pareto principle"

The "80-20 law", according to which 20% of all people receive 80% of all income, and 20% of the most affluent 20% receive 80% of that 80%, and so on, holds precisely when the Pareto index is α = log₄5, approximately 1.161. Moreover, the following have been shown to be mathematically equivalent:

• Income is distributed according to a Pareto distribution with index α > 1.
• There is some number 0 ≤ p ≤ 1/2 such that 100p% of all people receive 100(1 − p)% of all income, and similarly for every real (not necessarily integer) n > 0, 100pⁿ% of all people receive 100(1 − p)ⁿ% of all income.

This does not apply only to income, but also to wealth, or to anything else that can be modeled by this distribution.

This excludes Pareto distributions in which 0 < α ≤ 1, which, as noted above, have infinite expected value, and so cannot reasonably model income distribution.

Pareto, Lorenz, and Gini

Lorenz curves for a number of Pareto distributions. The case α = ∞ corresponds to perfectly equal distribution (G = 0) and the α = 1 line corresponds to complete inequality (G = 1)

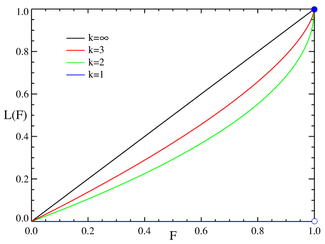
The Lorenz curve is often used to characterize income and wealth distributions. For any distribution, the Lorenz curve L(F) is written in terms of the PDF ƒ or the CDF F as

$L(F)={\frac {\int _{x_{\mathrm {m} }}^{x(F)}xf(x)\,dx}{\int _{x_{\mathrm {m} }}^{\infty }xf(x)\,dx}}={\frac {\int _{0}^{F}x(F')\,dF'}{\int _{0}^{1}x(F')\,dF'}}$

where x(F) is the inverse of the CDF. For the Pareto distribution,

$x(F)={\frac {x_{\mathrm {m} }}{(1-F)^{1/\alpha }}}$

and the Lorenz curve is calculated to be

$L(F)=1-(1-F)^{1-1/\alpha },\,$

where α must be greater than or equal to unity, since the denominator in the expression for L(F) is just the mean value of x. Examples of the Lorenz curve for a number of Pareto distributions are shown in the graph on the right.

The Gini coefficient is a measure of the deviation of the Lorenz curve from the equidistribution line which is a line connecting [0, 0] and [1, 1], which is shown in black (α = ∞) in the Lorenz plot on the right. Specifically, the Gini coefficient is twice the area between the Lorenz curve and the equidistribution line. The Gini coefficient for the Pareto distribution is then calculated to be

$G=1-2\int _{0}^{1}L(F)\,dF={\frac {1}{2\alpha -1}}$

(see Aaberge 2005).

Parameter estimation

The likelihood function for the Pareto distribution parameters α and x_m, given a sample x = (x₁, x₂, ..., x_n), is

$L(\alpha ,x_{\mathrm {m} })=\prod _{i=1}^{n}\alpha {\frac {x_{\mathrm {m} }^{\alpha }}{x_{i}^{\alpha +1}}}=\alpha ^{n}x_{\mathrm {m} }^{n\alpha }\prod _{i=1}^{n}{\frac {1}{x_{i}^{\alpha +1}}}.\!$

Therefore, the logarithmic likelihood function is

$\ell (\alpha ,x_{\mathrm {m} })=n\ln \alpha +n\alpha \ln x_{\mathrm {m} }-(\alpha +1)\sum _{i=1}^{n}\ln x_{i}.\!$

It can be seen that $\ell (\alpha ,x_{\mathrm {m} })$ is monotonically increasing with $x_{\mathrm {m} }$, that is, the greater the value of $x_{\mathrm {m} }$, the greater the value of the likelihood function. Hence, since $x\geq x_{\mathrm {m} }$, we conclude that

${\widehat {x}}_{\mathrm {m} }=\min _{i}{x_{i}}.$

To find the estimator for α, we compute the corresponding partial derivative and determine where it is zero:

${\frac {\partial \ell }{\partial \alpha }}={\frac {n}{\alpha }}+n\ln x_{\mathrm {m} }-\sum _{i=1}^{n}\ln x_{i}=0.$

Thus the maximum likelihood estimator for α is:

${\widehat {\alpha }}={\frac {n}{\sum _{i}\left(\ln x_{i}-\ln {\widehat {x}}_{\mathrm {m} }\right)}}.$

The expected statistical error is:

$\sigma ={\frac {\widehat {\alpha }}{\sqrt {n}}}.$

Graphical representation

The characteristic curved 'long tail' distribution when plotted on a linear scale, masks the underlying simplicity of the function when plotted on a log-log graph, which then takes the form of a straight line with negative gradient.

Generating a random sample from Pareto distribution

Random samples can be generated using inverse transform sampling. Given a random variate U drawn from the uniform distribution on the unit interval (0, 1), the variate T given by

$T={\frac {x_{\mathrm {m} }}{U^{1/\alpha }}}$

is Pareto-distributed.

Bounded Pareto distribution

Bounded Pareto

Parameters	$L>0\,$ location (real) $H>L\,$ location (real) $\alpha >0\,$ shape (real)
Support	$L\leqslant x\leqslant H\,$
PDF	${\frac {\alpha L^{\alpha }x^{-\alpha -1}}{1-\left({\frac {L}{H}}\right)^{\alpha }}}$
CDF	${\frac {1-L^{\alpha }x^{-\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}$
Mean	${\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot \left({\frac {\alpha }{\alpha -1}}\right)\cdot \left({\frac {1}{L^{\alpha -1}}}-{\frac {1}{H^{\alpha -1}}}\right),\alpha \neq 1$
Median	$L\left(1-{\frac {1}{2}}\left(1-\left({\frac {L}{H}}\right)^{\alpha }\right)\right)^{-{\frac {1}{\alpha }}}$
Variance	${\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot \left({\frac {\alpha }{\alpha -2}}\right)\cdot \left({\frac {1}{L^{\alpha -2}}}-{\frac {1}{H^{\alpha -2}}}\right),\alpha \neq 2$

The bounded Pareto distribution has three parameters α, L and H. As in the standard Pareto distribution α determines the shape. L denotes the minimal value, and H denotes the maximal value. (The Variance in the table on the right should be interpreted as 2nd Moment).

The probability density function is

${\frac {\alpha L^{\alpha }x^{-\alpha -1}}{1-\left({\frac {L}{H}}\right)^{\alpha }}}$

where L ≤ x ≤ H, and α > 0.

Generating bounded Pareto random variables

If U is uniformly distributed on (0, 1), then

$\left(-{\frac {UH^{\alpha }-UL^{\alpha }-H^{\alpha }}{H^{\alpha }L^{\alpha }}}\right)^{-{\frac {1}{\alpha }}}$

is bounded Pareto-distributed.

Symmetric Pareto distribution

The symmetric Pareto distribution can be defined by the probability density function:

$f(x;\alpha ,x_{\mathrm {m} })={\begin{cases}(\alpha x_{\mathrm {m} }^{\alpha }/2)|x|^{-\alpha -1}&{\text{for }}|x|>x_{\mathrm {m} }\\0&{\text{otherwise}}.\end{cases}}$

The density is zero for x between $-x_{\mathrm {m} }$ and $x_{\mathrm {m} }$. It has a similar shape to a Pareto distribution for $x>x_{\mathrm {m} }$ while looking like an inverted Pareto distribution for $x<x_{\mathrm {m} }$

See also

• Cumulative frequency analysis
• Pareto analysis
• Pareto efficiency
• Pareto interpolation
• Pareto principle
• The Long Tail
• Traffic generation model

References

• Barry C. Arnold (1983). Pareto Distributions. International Co-operative Publishing House. ISBN 0-899974-012-1. {{cite book}}: Check |isbn= value: length (help)
• Christian Kleiber and Samuel Kotz (2003). Statistical Size Distributions in Economics and Actuarial Sciences. Wiley. ISBN 0-471-15064-9.
• M. O. Lorenz (1905). "Methods of measuring the concentration of wealth". Publications of the American Statistical Association. 9 (70): 209–219. Bibcode:1905PAmSA...9..209L. doi:10.2307/2276207.
• Pareto V (1965) "La Courbe de la Repartition de la Richesse" (Originally published in 1896). In: Busino G, editor. Oevres Completes de Vilfredo Pareto. Geneva: Librairie Droz. pp. 1–5.

External links

• The Pareto, Zipf and other power laws / William J. Reed – PDF
• Gini's Nuclear Family / Rolf Aabergé. – In: International Conference to Honor Two Eminent Social Scientists, May, 2005 – PDF
• syntraf1.c is a C program to generate synthetic packet traffic with bounded Pareto burst size and exponential interburst time.
• "Self-Similarity in World Wide Web Traffic: Evidence and Possible Causes" /Mark E. Crovella and Azer Bestavros