Theta model

Dynamics of the theta model on the unit circle. Blue denotes a stable fixed point; Green denotes an unstable fixed point. By varying the input parameter, the two equilibria collide and form a stable limit cycle; Gray arrows indicate that the points are attracting in $\mathbb {R} ^{2}$; Black arrows indicate the direction of movement along the unit circle.

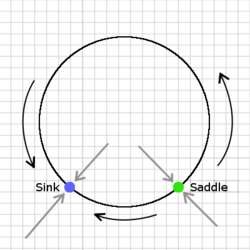
The theta model (otherwise known as the Ermentrout-Kopell canonical model) is a mathematical model" (in particular, a "biological neuron model") developed to describe the behavior of action potentials in neurons. In particular, the model helps elucidate a process involving a rapid series of action potentials known as bursts. Bursts are categorized into three main classes: square wave bursting, parabolic bursting, and elliptic bursting (Lee, 2005; Vries, 1998). The theta model was built to describe parabolic bursting. Parabolic bursting is characterized by a series of bursts that are modulated by a slower, underlying oscillation (Ermentrout and Kopell, 1986), where the slower oscillation periodically inhibits bursting so that bursts are separated by periods of quiescence.

The model has just one state variable, as opposed to four in the Hodgkin-Huxley model and two in the Morris-Lecar model (Ermentrout and Terman, 2010). This single state variable and the simple equations that govern its behavior make it relatively easy to produce analytic, or closed-form, solutions (including an explicit expression for the phase response curve). The dynamics of the model take place on the unit circle and are governed by two cosine functions and a real-valued input function (Ermentrout and Kopell, 1986).

The quadratic integrate and fire (QIF) model is a close cousin of the theta model and differs from the theta model by only by a change of variables (Brunel and Latham 2003; Ermentrout, 2008; Gielen et. al., 2010; Latham et. al. 2000; Richardson, 2008). Thus, mathematical analyses in systems which require the QIF model are sometimes performed using the theta model (Rozenberg et. al., 2010) and vice-versa (Kopell and Ermentrout, 2004; Latham et. al. 2000), since both models offer some advantage over the other in various contexts.

Despite its simplicity, the theta model offers enough complexity in its dynamics that it has been used for theoretical neuroscience research (Börgers et. al., 2008; Osan et.al., 2002) as well as in research beyond biology, such as in artificial intelligence (McKennoch et. al., 2008).

Background and History

A model of pre-Bötzinger complex neuron. The neuron bursts periodically with tonic noise input. The pre-Bötzinger complex is a region in the brain stem responsible for maintaining breathing rhythms. This is an example of a square-wave burster (Lee, 2005)

Bursting is "an oscillation in which an observable [part] of the system, such as voltage or chemical concentration, changes periodically between an active phase of rapid spike oscillations (the fast sub-system) and a phase of quiescence" (Bertram et. al. 1995). Bursting comes in three distinct forms: square wave bursting, parabolic bursting, and elliptic bursting (Lee, 2005; Vries, 1998). There exist some models that do not fit neatly into these categories by qualitative observation, but it is possible to sort such models by their topology (i.e. such models can be sorted "by the structure of the fast subsystem") (Bertram et. al. 1995).

All three forms of bursting are capable of beating and periodic bursting (Plant and Kim 1976). Periodic bursting (or just bursting) is of more interest because many phenomena are controlled by, or arise from, bursting. For example, bursting due to a changing membrane potential is common in various neurons, including but not limited to cortical chattering neurons, thalamacortical neurons, (Izhikevich, 2006), and pacemaker neurons. Pacemakers in general are known to burst and synchronize as a population, thus generating a robust rhythm that can maintain repetitive tasks like breathing, walking, and eating (Marder and Calabrese, 1996; Stein et al., 1997). Beating occurs when a cell bursts continuously with no periodic quiescent periods (Lechner et. al. 1996), but beating is often considered to be an extreme case and is rarely of primary interest.

Bursting cells are important for motor generation and synchronization (Izhikevich, 2006). For example, the pre-Bötzinger complex in the mammalian brain stem contains many bursting neurons that control autonomous breathing rhythms (Butera et. al. 1999; Del Negro et. al. 2002). Various neocortical neurons (i.e. cells of the neocortex) are capable of bursting, which "contribute significantly to [the] network behavior [of neocortical neurons]" (Connors and Gutnick, 1990). The R15 neuron of the abdominal ganglion in Aplyisa, hypothesized to be a neurosecretory cell (i.e. a cell that produces hormones), is known to produce bursts characteristic of neurosecretory cells (Adams and Benson, 1985). In particular, it is known to produce parabolic bursts.

Since many biological processes involve bursting behavior, there is a wealth of various bursting models in scientific literature. For instance, there exist several models for interneurons (Erisir et. al. 1999) and cortical spiking neurons (Izhikevich, 2004). However, the literature on parabolic bursting models is relatively scarce.

Parabolic bursting models are mathematical models that mimic parabolic bursting in real biological systems. Each burst of a parabolic burster has a characteristic feature in the burst structure itself - the frequency at the beginning and end of the burst is low relative to the frequency in the middle of the burst (Lee, 2005). A frequency plot of one burst resembles a parabola, hence the name "parabolic burst". Furthermore, unlike elliptic or square-wave bursting, there is a slow modulating wave which, at its peak, excites the cell enough to generate a burst and inhibits the cell in regions near its minimum. As a result, the neuron periodically transitions between bursting and quiescence.

Parabolic bursting has been studied most extensively in the R15 neuron, which is one of six types of neurons of the Aplysia abdominal ganglion (Faber and Klee) and one of thirty neurons comprising the abdominal ganglion (Kandel et. al. 1967). The Aplysia abdominal ganglion was studied and extensively characterized because its relatively large neurons and proximity of the neurons to the surface of the ganglion made it an ideal and "valuable preparation for cellular electrophysical studies" (Frazier et. al. 1967).

Early attempts to model parabolic bursting were for specific applications, often related to studies of the R15 neuron in the Aplysia abdominal ganglion. This is especially true of R. E. Plant (1978, 1979) and Carpenter (1979), whose combined works comprise the bulk of parabolic bursting models prior to Ermentrout and Kopell's canonical model.

Though there was no specific mention of the term "parabolic bursting" in Plant's papers, Plant's model(s) do involve a slow, modulating oscillation which control bursting in the model(s) (Plant, 1978 and 1979). This is, by definition, parabolic bursting. Both of Plant's papers on the topic involve a model derived from the Hodgkin-Huxley equations and include extra conductances, which only add to the complexity of the model.

Carpenter (1979) developed her model primarily for a square wave burster. The model is capable of producing a small variety of bursts, including bursts where the spike frequency change from high to low from the beginning to the end of a burst, and also where the spike frequency change from low to high. This square wave bursting model produced parabolic bursts as a consequence of adding an extra conductance, but the model applied to only spacial propagation down axons and not situations where oscillations are limited to a small region in space (i.e. it was not suited for "space-clamped" situations).

The lack of a simple, generalizable, space-clamped, parabolic bursting model motivated Ermentrout and Kopell to develop the theta model.

Characteristics of the model

General Equations

It is possible to describe very many types of parabolic bursting cells by deriving a very simple mathematical model, called a canonical model. Derivation of the Ermentrout and Kopell canonical model will begin with the general form for parabolic bursting, and notation will be fixed to clarify the discussion. The letters $f$, $g$, $h$, $I$ are reserved for functions; $x$, $y$, $\theta$ for state variables (which may be vectors whose entries are state variables); and $\varepsilon$, $p$, $q$ and other letters for scalars.

In the following generalized system of equations for parabolic bursting, the values of $f$ describe the membrane potential and ion channels, typical of many conductance-based biological neuron models. Slow oscillations are controlled by $h$ (and so ultimately controlled by $y$). These slow oscillations can be, for example, slow fluctuations in calcium concentration inside a cell. The function $g$ couples ${\dot {y}}$ to ${\dot {x}}$, thereby allowing the second system, ${\dot {y}}$, to influence the behavior of the first system, ${\dot {x}}$. In more succinct terms, "$x$ generates the spikes and $y$ generates the slow waves" (Ermentrout and Kopell, 1986). The equations are:

${\dot {x}}=f(x)+\varepsilon ^{2}g(x,y,\varepsilon )$,

${\dot {y}}=\varepsilon h(x,y,\varepsilon )$,

where $x$ is a vector with $p$ entries (i.e. $x\in \mathbb {R} ^{p}$), $y$ is a vector with $q$ entries (i.e. $y\in \mathbb {R} ^{q}$), $\varepsilon$ is small and positive, and $f$, $g$, $h$ are smooth (i.e. infinitely differentiable) (Ermentrout and Kopell, 1986). Additional constraints are required to guarantee parabolic bursting. First, ${\dot {x}}=f(x)$ must produce a circle in phase space that is invariant, meaning it does not change under certain transformations. This circle must also be attracting in $\mathbb {R} ^{2}$ with a critical point located at $x=0$. The second criterion requires that when ${\dot {y}}=h(0,y,0)$, there exists a stable limit cycle solution. These criteria can be summarized by the following points:

1. When $\varepsilon =0$, ${\dot {x}}=f(x)$ "has an attracting invariant circle with a single critical point", with the critical point located at $x=0$, and
2. When $x=0\;$, ${\dot {y}}=h(0,y,0)$ has a stable limit cycle solution. (Ermentrout and Kopell, 1986)

Under these assumptions, the generalized system of equations for parabolic bursters converge to the theta model.

Model Equations and Properties

The theta model is a reduction of the generalized system from the previous section and takes the form

${\frac {d\theta }{dt}}=1-\cos \theta +(1+\cos \theta )I(t),\;\;\;\theta \in S^{1}$.

This model is one of the simplest excitable neuron models (McKennoch et. al. 2008). The state variable $\theta$ represents the angle in radians, and the input function, $I(t)$, is typically periodic. Whenever $\theta$ is at a particular angle (namely $\theta =\pi$), the model produces a spike (Ermentrout 2008; McKennoch et. al. 2008).

The theta model is capable of a single saddle-node bifurcation and can be shown to be the "normal form for the saddle-node on a limit cycle bifurcation" (SNIC) (Ermentrout 2008). When $(I<0)$, the system is excitable (i.e. given an appriate perturbation the system will produce a spike). When viewed in the plane ($\mathbb {R} ^{2}$), the unstable critical point is actually a saddle point because $S^{1}$ is attracting in $\mathbb {R} ^{2}$. On the other hand, when $(I>0)$, ${\dot {\theta }}$ is also positive, and the system will give rise to a limit cycle. Therefore, the bifurcation point is located at $I(t)=0$.

Near the bifurcation point, the theta model resembles the quadratic integrate-and-fire model:

${\frac {dx}{dt}}=x^{2}+I$.

For I > 0, the solutions "blow up" rather quickly. By resetting the trajectory $x(t)\;$ to $-\infty$when it reaches $+\infty$, the total period is then

$T={\frac {\pi }{\sqrt {I}}}$.

Therefore, the period diverges as $I\rightarrow 0$ for $I>0\;$ and the frequency converges to zero (Ermentrout 2008).

Example

When $I(t)$ is some slow wave which can be both negative and positive, the system is capable of producing parabolic bursts. Consider the simple example $I(t):=\sin(\alpha t)$, where $\alpha$ is relatively small. Then for $\alpha t\in (0,\pi )$, $I(t)$ is strictly positive and $\theta$ makes multiple passes through the angle $\pi$, resulting in multiple bursts. Note that whenever $\alpha t$ is near zero or $\pi$, the theta neuron will spike at relatively a low frequency, and whenever $\alpha t$ is near $\alpha t=\pi /2$ the neuron will spike with very high frequency. When $\alpha t=\pi$, the frequency of spikes is zero since the period is infinite since $\theta$ can no longer pass through $\theta =\pi$. Finally, for $\alpha t\in (\pi ,2\pi )$, the neuron is excitable and will no longer burst. This qualitative description highlights the characteristics that make the theta model a parabolic bursting model. Not only does the model have periods of quiescence between bursts which are modulated by a slow wave, but the frequency of spikes at the beginning and end of each burst is high relative to the frequency at the middle of the burst.

Derivation

The derivation comes in the form of two lemmas in Ermentrout and Kopell (1986). Lemma 1, in summary, states that when viewing the general equations above in a subset $S^{1}\times \mathbb {R} ^{2}$, the equations take the form:

${\dot {x_{1}}}={\overline {f}}(x_{1})+\varepsilon ^{2}{\overline {g}}(x_{1},y,\varepsilon )\;\;\;\;\;\;x_{1}\in S^{1}$,

${\dot {y}}=\varepsilon {\overline {h}}(x_{1},y,\varepsilon )\;\;\;\;\;\;y\in \mathbb {R} ^{q}$.

By lemma 2 in Ermentrout and Kopell 1986, "There exists a change of coordinates... and a constant, c, such that in new coordinates, the two equations above converge pointwise as $\varepsilon \rightarrow 0$ to the equations

${\dot {\theta }}=(1-\cos \theta )+(1+\cos \theta ){\overline {g}}(0,y,0)$,

${\dot {y}}={\frac {1}{c}}{\overline {h}}(0,y,0)$,

for all $\theta \neq \pi$. Convergence is uniform except near $\theta =\pi$." (Ermentrout and Kopell, 1986). By letting $I(t):={\overline {g}}(0,y,0)$, resemblance to the theta model is obvious.

Phase Response Curve

The phase response curve of the theta model with Z = 1. Since perturbations always result in a phase advance, this is a type 1 PRC.

In general, given a scalar phase model of the form

${\dot {\theta }}=f(\theta )+g(\theta )S(t)$,

where $S(t)$ represents the purturbation current, it is possible to derive a closed form solution for the phase response curve (PRC).

The theta model is a special case of such an oscillator, so it is easy to produce a closed-form solution for the PRC. The theta model is recovered by defining $f$ and $g$ as

$f(\theta )=(1-\cos \theta )+I(1+\cos \theta )\;$,

$g(\theta )=(1+\cos \theta )\;$.

In the appendix of Ermentrout 1996, the PRC is shown to be $Z(\theta )=K(1+\cos \theta )\;$.

Similar Models

Plant's Model

The authors of Soto-Treviño et. al. (1996) discuss in great detail the similarities between Plant's (1976) model and the theta model. At first glance, the mechanisms of bursting in both systems are very different: In Plant's model, there are two slow oscillations - one for conductance of a specific current and one for the concentration of calcium. The calcium oscillations are active only when the membrane potential is capable of oscillating. This contrasts heavily against the theta model in which one slow wave modulates the burst of the neuron and the slow wave has no dependence upon the bursts. Despite these differences, the theta model is shown to have the same "mathematical mechanics" as Plant's (1976) model by a series of coordinate transformations. In the process, Soto-Trevino, et al. discovered that the theta model was more general than originally believed.

Quadratic Integrate-and-Fire

The quadratic integrate-and-fire (QIF) model was created by Latham et. al. in 2000 to explore the many questions related to networks of neurons with low firing rates. It was unclear to Latham et. al. why networks of neurons with "standard" parameters were unable to generate sustained low frequency firing rates, while networks with low firing rates were often seen in biological systems.

According to Gerstner and Kistler (2002), the quadratic integrate-and-fire (QIF) model is given by the following differential equation:

$\tau {\dot {u}}=a_{0}(u-u_{rest})(u-u_{c})+R_{m}I$,

where $a_{0}$ is a strictly positive scalar, $u$ is the membrane potential, $u_{rest}$ is the resting potential $u_{c}$ is the minimum potential necessary for the membrane to produce an action potential, $R_{m}$ is the membrane resistance, $\tau$ the membrane time constant and $u_{c}>u_{rest}$. When there is no input current (i.e. $I=0$), the membrane potential quickly returns to rest following a perturbation. When the input current, $I$, is large enough, membrane potential ($u$) surpasses its firing threshold and the system blows up to infinity in finite time. To allow for numerical simulations, Latham et. al. (2000) reset the voltage from $+20$mV to $-80$mV (Latham et. al. 2000). This voltage reset constitutes an action potential.

The theta model is very similar to the QIF model since the theta model differs from the QIF model by means of a simple coordinate transform (Brunel and Latham 2003; Latham et. al. 2000). By scaling the voltage appropriately and letting $\Delta I$ be the change in current from the minimum current required to elicit a spike, the QIF model can be rewritten in the form

${\dot {u}}=u^{2}+\Delta I$.

Similarly, the theta model can be rewritten as

${\dot {\theta }}=1-\cos \theta +(1+\cos \theta )\Delta I$.

The following proof will show that the QIF model becomes the theta model given an appropriate choice for the coordinate transform.

Define $u(t)=\tan(\theta /2)\;$. Recall that $d\tan(x)/dx=1/\cos ^{2}(x)$, so taking the derivative yields

${\dot {u}}={\frac {1}{\cos ^{2}(\theta /2)}}{\frac {1}{2}}{\dot {\theta }}=u^{2}+\Delta I$.

An additional substitution and rearranging in terms of $\theta$ yields

${\dot {\theta }}=2[\cos ^{2}(\theta /2)\tan ^{2}(\theta /2)+\cos ^{2}(\theta /2)\Delta I]=2[\sin ^{2}(\theta /2)+\cos ^{2}(\theta /2)\Delta I]$.

Using the trigonometric identities $\cos ^{2}(x/2)={\frac {1+\cos(2x)}{2}}$, $\sin ^{2}(x/2)={\frac {1-\cos(2x)}{2}}$ and ${\dot {\theta }}$ as defined above, we have that

${\dot {\theta }}=2[{\frac {1-\cos \theta }{2}}+({\frac {1+\cos \theta }{2}})\Delta I]=1-\cos \theta +(1+\cos \theta )\Delta I$.

Therefore, there exists a change of coordinates, namely $u(t)=\tan(\theta /2)\;$, which transforms the QIF model into the theta model. The reverse transformation also exists, and is attained by taking the inverse of the first transformation.

Applications

Neuroscience

Lobster Stomatogastric Ganglion

Though the theta model was originally used to model slow cytoplasmic oscillations that modulate fast membrane oscillations in a single cell, Ermentrout and Kopell (1986) found that the theta model could be applied just as easily to systems of two electrically coupled cells such that the slow oscillations of one cell modulates the bursts of the other. Such cells serve as the central pattern generator (CPG) of the pyloric system in the lobster stomatograstic ganglion (Marder and Eisen 1984). In such a system, a slow oscillator, called the anterior burster (AB) cell, modulates the bursting cell called the pyloric dilator (PD), resulting in parabolic bursts (Ermentrout and Kopell, 1986).

Visual Cortex

A group lead by Boergers (2008), used the theta model to explain why exposure to multiple simultaneous stimuli can reduce the response of the visual cortex below the normal response from a single (preferred) stimulus. Their computational results showed that this may happen due to strong stimulation of a large group of inhibitory neurons. This effect not only inhibits neighboring populations, but has the extra consequence of leaving the inhibitory neurons in disarray, thus increasing the effectiveness of inhibition.

Theta Networks

Osan et. al. (2002) found that in a network of theta neurons, there exist two different types of waves that propagate smoothly over the network, given a sufficiently large coupling strength. Such traveling waves are of interest because they are frequently observed in pharmacologically treated brain slices, but are hard to measure in intact animals brains (Osan et. al. 2002). The authors used a network of theta models in favor of a network of leaky integrate-and-fire (LIF) models due to two primary advantages: first, the theta model is continuous, and second, the theta model retains information about "the delay between the crossing of the spiking threshold and the actual firing of an action potential". The LIF fails to satisfy both conditions.

Artificial Intelligence

Steepest Gradient Descent Learning Rule

The theta model can also be applied to research beyond the ream of biology. McKennoch et. al. (2008) derived a steepest gradient descent learning rule based on theta neuron dynamics. Their model is based on the assumption that "intrinsic neuron dynamics are sufficient to achieve consistent time coding, with no need to involve the precise shape of postsynaptic currents..." contrary to similar models like SpikeProp and Tempotron, which depend heavily on the shape of the postsynaptic potential (PSP). Not only could the multilayer theta network perform just about as well as Tempotron learning, but the rule trained the multilayer theta network to perform certain tasks neither SpikeProp nor Tempotron were capable of.

Limitations

Near the bifurcation, the theta model rapidly diverges to infinity in finite time, so the voltage must be reset from $-\infty$ to $+\infty$ to complete an action potential. On the other hand, the QIF model is reset from a finite value to another finite value, so it may be advantageous to use the QIF in place of the theta model for numerical simulations (Latham et. al. 2000).

Furthermore, according to Kopell and Ermentrout (2004), another limitation of the theta lies in its relative difficulty in electrically coupling two theta neurons. It is possible to create large networks of theta neurons and much research has been done with such networks, but it may be advantageous to use Quadratic Integrate-and-Fire (QIF) neurons, which allow for electrical coupling in a "straightforward way".

See Also/External Links

• Biological neuron model
• Computational neuroscience
• Ermentrout and Kopell canonical model on Scholarpedia
• FitzHugh-Nagumo model
• Hodgkin-Huxley model
• Neuroscience
• Plant Model on Scholarpedia

References

1. Adams, W., and J. A. Benson. "The Generation and Modulation of Endogenous Rhythmicity in the Aplysia Bursting Pacemaker Neurone R15." Progress in Biophysics and Molecular Biology 46.1 (1985): 1-49. Print.
2. Berridge, M. J., and P. E. Rapp. "A Comparative Survey of the Function, Mechanism and Control of Cellular Oscillators." J. Exp. Biol 81 (1979): 217-79.
3. Bertram, R., M. Butte, T. Kiemel, and A. Sherman. "Topological and Phenomenological Classification of Bursting Oscillations." Bulletin of Mathematical Biology 57.3 (1995): 413-39. Print.
4. Börgers C., Epstein S., and Kopell N., Gamma Oscillations Mediate Stimulus Competition and Attentional Selection in a Cortical Network Model Proceedings of the National Academy of Sciences of the United States of America, Vol. 105, No. 46 (Nov. 18, 2008), pp. 18023-18028
5. Brunel, Nicolas, and Peter E. Latham. "Firing Rate of the Noisy Quadratic Integrate-and-Fire Neuron." Neural Computation 15.10 (2003): 2281-306.
6. Butera, J. R., J. Rinzel, and J. C. Smith. "Models of Respiratory Rhythm Generation in the Pre-Bötzinger Complex. I. Bursting Pacemaker Neurons." J. Neurophysiol 82 (1999): 398-415.
7. Carpenter, Gail A. "Bursting Phenomena in Excitable Membranes." SIAM Journal on Applied Mathematics 36.2 (1979): 334. Print.
8. Connors, B., and M. Gutnick. "Intrinsic Firing Patterns of Diverse Neocortical Neurons." Trends in Neurosciences 13.3 (1990): 99-104. Print.
9. Del Negro, C. A., C. G. Wilson, R. J. Butera, and J. C. Smith. "Periodicity, Mixed-mode Oscillations, and Quasiperiodicity in a Rhythm-generating Neural Network." Biophys J. 82 (2002): 206-14.
10. Erisir, A., D. Lau, B. Rudy, and S. Leonard. "Function of Specific K+ Channels in Sustained High-frequency Firing of Fast-spiking Neocortical Cells." J. Neurophysiol 82 (1999): 2476-489. Print.
11. Ermentrout B. "Ermentrout-Kopell Canonical Model." Scholarpedia 3.3 (2008): 1398.
12. Ermentrout B. "Type I Membranes, Phase Resetting Curves, and Synchrony." Neural Computation 8.5 (1996): 979-1001. Print.
13. Ermentrout B, Kopell N. "Parabolic bursting in an excitable system coupled with a slow oscillation." SIAM-J.-Appl.-Math, 1986
14. Ermentrout B, Terman DH. Mathematical Foundations of Neuroscience. New York: Springer, 2010.
15. Faber D, Klee M. "Membrane Characteristics of Bursting Pacemaker Neurons in Aplysia." Nature New Biology 240 (1972): 29-31. Print.
16. Frazier, W. T., E. R. Kandel, Irving Kupfermann, Rafiq Waziri, and R. E. Coggeshall. "Morphological and Functional Properties of Identified Neurons in the Abdominal Ganglion of Aplysia Californica." J. Neurophysiol 30.6 (1967): 1288-351. Print.
17. Gerstner, Wulfram, and Werner M. Kistler. Spiking Neuron Models: Single Neurons, Populations, Plasticity. Cambridge, U.K.: Cambridge UP, 2002. Print.
18. Gielen, Stan, Martin Krupa, and Magteld Zeitler. "Gamma Oscillations as a Mechanism for Selective Information Transmission." Biological Cybernetics 103.2 (2010): 151-65.
19. Izhikevich, E.M. "Bursting." Scholarpedia 1.3 (2006): 1300. Print.
20. Izhikevich, E.M. "Which Model to Use for Cortical Spiking Neurons?" IEEE Transactions on Neural Networks 15.5 (2004): 1063-070. Print.
21. Kandel, E. R., W. T. Frazier, R. Waziri, and R. E. Coggeshall. "Direct and Common Connections Among Identified Neurons in Aplysia." J. Neurophysiol 30.6 (1967): 1352-376. Print.
22. Keener, James P., and James Sneyd. Mathematical Physiology. New York: Springer, 2009. Print.
23. Kopell N. and Ermentrout B., "Chemical and Electrical Synapses Perform Complementary Roles in the Synchronization of Interneuronal Networks." Proceedings of the National Academy of Sciences 101.43 (2004): 15482-5487.
24. Latham, P. E., B. J. Richmond, P. G. Nelson, and S. Nirenberg. "Intrinsic Dynamics in Neuronal Networks. I. Theory." Journal of Neurophysiol. 88.2 (2000): 808-27. Print.
25. Lechner, H. A., D. A. Baxter, J. W. Clark, and J. H. Byrne. "Bistability and Its Regulation By Serotonin in the Endogenously Bursting Neuron Rl5 in Aplysia." J Neurophys 75.2 (1996): 957-62.
26. Lee, E. "Stability Analysis Of Bursting Models." Journal of the Korean Mathematical Society 42.4 (2005): 827-45.
27. Marder, E., and J. S. Eisen. "Electrically Coupled Pacemaker Neurons Respond Differently to Same Physiological Inputs and Neurotransmitters." Journal of Neurophysiology 51.6 (1984): 1362-374. Print.
28. Marder, E., and R. L. Calabrese. "Principles of Rhythmic Motor Pattern Generation." Physiol. Rev. 76 (1996): 687-717.
29. McKennoch, S., Voegtlin T., and Bushnell L. "Spike-Timing Error Backpropagation in Theta Neuron Networks." Neural Computation 0.0 (2008): 080804143617793-37.
30. Osan R., Rubin J., and Ermentrout B., Regular Traveling Waves in a One-Dimensional Network of Theta Neurons, SIAM Journal on Applied Mathematics, Vol. 62, No. 4 (Apr., 2002), pp. 1197-1221
31. Plant, R. "The Effects of Calcium++ on Bursting Neurons. A Modeling Study." Biophysical Journal 21.3 (1978): 217-37. Print.
32. Plant, R. Kim, M. "Mathematical Description of a Bursting Pacemaker Neuron by a Modification of the Hodgkin-Huxley Equations." Biophysical Journal 16.3 (1976): 227-44. Print.
33. Richardson, Magnus J. E. "Spike-train Spectra and Network Response Functions for Non-linear Integrate-and-fire Neurons." Biological Cybernetics 99.4-5 (2008): 381-92.
34. Rozenberg, Grzegorz, Thomas Bäck, and Joost N. Kok. Handbook of Natural Computing. Berlin: Springer, 2010. Print. (Chapter: Computing with Spiking Neuron Networks)
35. Soto-Treviño, C., N. Kopell, and D. Watson. "Parabolic Bursting Revisited." Journal of Mathematical Biology 35.1 (1996): 114-28.
36. Stein, P., S. Grillner, A. Selverston, and D. Stuart. "Neurons, Networks, and Motor Behavior." MIT Press (1997). Print.
37. Vries, G. De. "Multiple Bifurcations in a Polynomial Model of Bursting Oscillations." Journal of Nonlinear Science 8.3 (1998): 281-316. Print.

Further Reading

• Ermentrout, Bard, and David H. Terman. Mathematical Foundations of Neuroscience. New York: Springer, 2010. ISBN 978-0387877075
• Ermentrout B, Kopell N. "Parabolic bursting in an excitable system coupled with a slow oscillation." SIAM-J.-Appl.-Math, 1986
• Keener, James P., and James Sneyd. Mathematical Physiology. New York: Springer, 2009. ISBN 978-0387983813
• Plant, R. Kim, M. "Mathematical Description of a Bursting Pacemaker Neuron by a Modification of the Hodgkin-Huxley Equations." Biophysical Journal 16.3 (1976): 227-44. Print.
• Stein, P., S. Grillner, A. Selverston, and D. Stuart. "Neurons, Networks, and Motor Behavior." MIT Press (1997). ISBN 978-0262692274