Log-Cauchy distribution: Difference between revisions
m ISBNs (Build J/) |
|||
| Line 33: | Line 33: | ||
\end{align}</math> |
\end{align}</math> |
||
where <math> \mu</math> is a [[real number]] and <math> \sigma >0</math>.<ref name=robust>{{cite web|title=Applied Robust Statistics|url=http://www.math.siu.edu/olive/run.pdf|author=Olive, D.J.|date=June 23, 2008|publisher=Southern Illinois University|page=86|accessdate=2011-10-18}}</ref><ref name=stochastic>{{cite book|title=Statistical analysis of stochastic processes in time|author=Lindsey, J.K.|page=33, 50, 56, 62, 145|year=2004|publisher=Cambridge University Press|isbn= |
where <math> \mu</math> is a [[real number]] and <math> \sigma >0</math>.<ref name=robust>{{cite web|title=Applied Robust Statistics|url=http://www.math.siu.edu/olive/run.pdf|author=Olive, D.J.|date=June 23, 2008|publisher=Southern Illinois University|page=86|accessdate=2011-10-18}}</ref><ref name=stochastic>{{cite book|title=Statistical analysis of stochastic processes in time|author=Lindsey, J.K.|page=33, 50, 56, 62, 145|year=2004|publisher=Cambridge University Press|isbn=978-0-521-83741-5}}</ref> If <math>\sigma</math> is known, the [[scale parameter]] is <math>e^{\mu}</math>.<ref name=robust/> <math> \mu</math> and <math> \sigma</math> correspond to the [[location parameter]] and [[scale parameter]] of the associated Cauchy distribution.<ref name=robust/><ref name=hiv>{{cite book|title=Stochastic processes in epidemiology: HIV/AIDS, other infectious diseases|author=Mode, C.J. & Sleeman, C.K.|pages=29–37|year=2000|publisher=World Scientific|isbn=978-981-02-4097-4}}</ref> Some authors define <math> \mu</math> and <math> \sigma</math> as the [[location parameter|location]] and scale parameters, respectively, of the log-Cauchy distribution.<ref name=hiv/> |
||
For <math>\mu = 0</math> and <math>\sigma =1</math>, corresponding to a standard Cauchy distribution, the probability density function reduces to:<ref name=life/> |
For <math>\mu = 0</math> and <math>\sigma =1</math>, corresponding to a standard Cauchy distribution, the probability density function reduces to:<ref name=life/> |
||
| Line 56: | Line 56: | ||
==Properties== |
==Properties== |
||
The log-Cauchy distribution is an example of a [[heavy-tailed distribution]].<ref name=small>{{cite web|title=Laws of Small Numbers: Extremes and Rare Events|author=Falk, M., Hüsler, J. & Reiss, R.|page=80|year=2010|publisher=Springer|isbn= |
The log-Cauchy distribution is an example of a [[heavy-tailed distribution]].<ref name=small>{{cite web|title=Laws of Small Numbers: Extremes and Rare Events|author=Falk, M., Hüsler, J. & Reiss, R.|page=80|year=2010|publisher=Springer|isbn=978-3-0348-0008-2}}</ref> Some authors regard it as a "super-heavy tailed" distribution, because it has a heavier tail than a [[Pareto distribution]]-type heavy tail, i.e., it has a [[logarithmic growth|logarithmically decaying]] tail.<ref name=small/><ref>{{cite web|title=Statistical inference for heavy and super-heavy tailed distributions|url=http://docentes.deio.fc.ul.pt/fragaalves/SuperHeavy.pdf|author=Alves, M.I.F., de Haan, L. & Neves, C.|date= |
||
March 10, 2006}}</ref> As with the Cauchy distribution, none of the non-trivial [[moment (mathematics)|moments]] of the log-Cauchy distribution are finite.<ref name=life>{{cite book|title=Life distributions: structure of nonparametric, semiparametric, and parametric families|author=Marshall, A.W. & Olkin, I.|pages=443–444|year=2007|publisher=Springer|isbn= |
March 10, 2006}}</ref> As with the Cauchy distribution, none of the non-trivial [[moment (mathematics)|moments]] of the log-Cauchy distribution are finite.<ref name=life>{{cite book|title=Life distributions: structure of nonparametric, semiparametric, and parametric families|author=Marshall, A.W. & Olkin, I.|pages=443–444|year=2007|publisher=Springer|isbn=978-0-387-20333-1}}</ref> The [[mean]] is a moment so the log-Cauchy distribution does not have a defined mean or [[standard deviation]].<ref>{{cite web|title=Moment|url=http://mathworld.wolfram.com/Moment.html|publisher=[[Mathworld]]|accessdate=2011-10-19}}</ref><ref>{{cite web|title= |
||
Trade, Human Capital and Technology Spillovers: An Industry Level Analysis|author=Wang, Y.|page=14|publisher=Carleton University|accessdate=2011-10-19}}</ref> |
Trade, Human Capital and Technology Spillovers: An Industry Level Analysis|author=Wang, Y.|page=14|publisher=Carleton University|accessdate=2011-10-19}}</ref> |
||
The log-Cauchy distribution is [[Infinite divisibility (probability)|infinitely divisible]] for some parameters but not for others.<ref>{{cite web|title=On the Levy Measure of the Lognormal and LogCauchy Distributions|url=http://resources.metapress.com/pdf-preview.axd?code=gn16hw202rxh4q1g&size=largest|accessdate=2011-10-18|author=Bondesson, L.|journal=Methodology and Computing in Applied Probability|year=2003|pages=243–256|publisher=Kluwer Academic Publications}}</ref> Like the [[lognormal distribution]], [[log-t distribution|log-t or log-Student distribution]] and [[Weibull distribution]], the log-Cauchy distribution is a special case of the [[generalized beta distribution of the second kind]].<ref>{{cite book|title=Return distributions in finance|author=Knight, J. & Satchell, S.|page=153|year=2001|publisher=Butterworth-Heinemann|isbn= |
The log-Cauchy distribution is [[Infinite divisibility (probability)|infinitely divisible]] for some parameters but not for others.<ref>{{cite web|title=On the Levy Measure of the Lognormal and LogCauchy Distributions|url=http://resources.metapress.com/pdf-preview.axd?code=gn16hw202rxh4q1g&size=largest|accessdate=2011-10-18|author=Bondesson, L.|journal=Methodology and Computing in Applied Probability|year=2003|pages=243–256|publisher=Kluwer Academic Publications}}</ref> Like the [[lognormal distribution]], [[log-t distribution|log-t or log-Student distribution]] and [[Weibull distribution]], the log-Cauchy distribution is a special case of the [[generalized beta distribution of the second kind]].<ref>{{cite book|title=Return distributions in finance|author=Knight, J. & Satchell, S.|page=153|year=2001|publisher=Butterworth-Heinemann|isbn=978-0-7506-4751-9}}</ref><ref>{{cite book|title=Market consistency: model calibration in imperfect markets|author=Kemp, M.|page=|year=2009|publisher=Wiley|isbn=978-0-470-77088-7}}</ref> The log-Cauchy is actually a special case of the log-t distribution, similar to the Cauchy distribution being a special case of the [[Student's t distribution]] with 1 degree of freedom.<ref>{{cite book|title=Statistical distributions in scientific work: proceedings of the NATO Advanced Study Institute|author=MacDonald, J.B.|chapter=Measuring Income Inequality|page=169|editor=Taillie, C., Patil, G.P. & Baldessari, B.|year=1981|publisher=Springer|isbn=978-90-277-1334-6}}</ref><ref name=kleiber>{{cite book|title=Statistical Size Distributions in Economics and Actuarial Science|author=Kleiber, C. & Kotz, S.|pages=101–102, 110|year=2003|publisher=Wiley|isbn=978-0-471-15064-0}}</ref> |
||
Since the Cauchy distribution is a [[stable distribution]], the log-Cauchy distribution is a logstable distribution.<ref>{{cite journal|title=Distribution function values for logstable distributions|url=http://www.sciencedirect.com/science/article/pii/089812219390128I|doi=10.1016/0898-1221(93)90128-I|author=Panton, D.B.|accessdate=2011-10-18|date=May 1993|pages=17–24|volume=25|issue=9|journal=Computers & Mathematics with Applications}}</ref> Logstable distributions have [[pole (complex analysis)|poles]] at x=0.<ref name=kleiber/> |
Since the Cauchy distribution is a [[stable distribution]], the log-Cauchy distribution is a logstable distribution.<ref>{{cite journal|title=Distribution function values for logstable distributions|url=http://www.sciencedirect.com/science/article/pii/089812219390128I|doi=10.1016/0898-1221(93)90128-I|author=Panton, D.B.|accessdate=2011-10-18|date=May 1993|pages=17–24|volume=25|issue=9|journal=Computers & Mathematics with Applications}}</ref> Logstable distributions have [[pole (complex analysis)|poles]] at x=0.<ref name=kleiber/> |
||
| Line 68: | Line 68: | ||
==Uses== |
==Uses== |
||
In [[Bayesian statistics]], the log-Cauchy distribution can be used to approximate the [[improper prior|improper]] [[Harold Jeffreys|Jeffreys]]-Haldane density, 1/k, which is sometimes suggested as the [[prior distribution]] for k where k is a positive parameter being estimated.<ref>{{cite book|title=Good thinking: the foundations of probability and its applications|author=Good, I.J.|page=102|year=1983|publisher=University of Minnesota Press|isbn= |
In [[Bayesian statistics]], the log-Cauchy distribution can be used to approximate the [[improper prior|improper]] [[Harold Jeffreys|Jeffreys]]-Haldane density, 1/k, which is sometimes suggested as the [[prior distribution]] for k where k is a positive parameter being estimated.<ref>{{cite book|title=Good thinking: the foundations of probability and its applications|author=Good, I.J.|page=102|year=1983|publisher=University of Minnesota Press|isbn=978-0-8166-1142-3}}</ref><ref>{{cite book|title=Frontiers of Statistical Decision Making and Bayesian Analysis|page=12|author=Chen, M.|year=2010|publisher=Springer|isbn=978-1-4419-6943-9}}</ref> The log-Cauchy distribution can be used to model certain survival processes where significant [[outlier]]s or extreme results may occur.<ref name=stochastic/><ref name=hiv/><ref>{{cite journal|title=Some statistical issues in modelling pharmacokinetic data|author=Lindsey, J.K., Jones, B. & Jarvis, P.|url=http://onlinelibrary.wiley.com/doi/10.1002/sim.742/abstract|10.1002/sim.742|journal=Statistics in Medicine|date=September 2001|volume=20|issue=17-18|pages=2775–278|accessdate=2011-10-19|doi=10.1002/sim.742}}</ref> An example of a process where a log-Cauchy distribution may be an appropriate model is the time between someone becoming infected with [[HIV virus]] and showing symptoms of the disease, which may be very long for some people.<ref name=hiv/> It has also been proposed as a model for species abundance patterns.<ref>{{cite journal|title=LogCauchy, log-sech and lognormal distributions of species abundances in forest communities|url=http://www.sciencedirect.com/science/article/pii/S0304380004005587|author=Zuo-Yun, Y. et al|journal=Ecological Modelling|volume=184|issue=2-4|doi=10.1016/j.ecolmodel.2004.10.011|date=June 2005|accessdate=2011-10-18|pages=329–340}}</ref> |
||
==References== |
==References== |
||
Revision as of 08:57, 19 March 2012
|
Probability density function 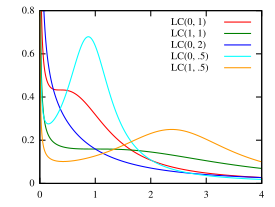 | |||
|
Cumulative distribution function 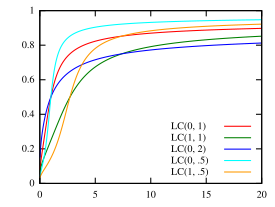 | |||
| Parameters |
(real) (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | does not exist | ||
| Median | |||
| Variance | infinite | ||
| Skewness | does not exist | ||
| Excess kurtosis | does not exist | ||
| MGF | does not exist | ||
In probability theory, a log-Cauchy distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Cauchy distribution. If X is a random variable with a Cauchy distribution, then Y = exp(X) has a log-Cauchy distribution; likewise, if Y has a log-Cauchy distribution, then X = log(Y) has a Cauchy distribution.[1]
Characterization
Probability density function
The log-Cauchy distribution has the probability density function:
where is a real number and .[1][2] If is known, the scale parameter is .[1] and correspond to the location parameter and scale parameter of the associated Cauchy distribution.[1][3] Some authors define and as the location and scale parameters, respectively, of the log-Cauchy distribution.[3]
For and , corresponding to a standard Cauchy distribution, the probability density function reduces to:[4]
Cumulative distribution function
The cumulative distribution function (cdf) when and is:[4]
Survival function
The survival function when and is:[4]
Hazard rate
The hazard rate when and is:[4]
The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.[4]
Properties
The log-Cauchy distribution is an example of a heavy-tailed distribution.[5] Some authors regard it as a "super-heavy tailed" distribution, because it has a heavier tail than a Pareto distribution-type heavy tail, i.e., it has a logarithmically decaying tail.[5][6] As with the Cauchy distribution, none of the non-trivial moments of the log-Cauchy distribution are finite.[4] The mean is a moment so the log-Cauchy distribution does not have a defined mean or standard deviation.[7][8]
The log-Cauchy distribution is infinitely divisible for some parameters but not for others.[9] Like the lognormal distribution, log-t or log-Student distribution and Weibull distribution, the log-Cauchy distribution is a special case of the generalized beta distribution of the second kind.[10][11] The log-Cauchy is actually a special case of the log-t distribution, similar to the Cauchy distribution being a special case of the Student's t distribution with 1 degree of freedom.[12][13]
Since the Cauchy distribution is a stable distribution, the log-Cauchy distribution is a logstable distribution.[14] Logstable distributions have poles at x=0.[13]
Estimating parameters
The median of the natural logarithms of a sample is a robust estimator of .[1] The median absolute deviation of the natural logarithms of a sample is a robust estimator of .[1]
Uses
In Bayesian statistics, the log-Cauchy distribution can be used to approximate the improper Jeffreys-Haldane density, 1/k, which is sometimes suggested as the prior distribution for k where k is a positive parameter being estimated.[15][16] The log-Cauchy distribution can be used to model certain survival processes where significant outliers or extreme results may occur.[2][3][17] An example of a process where a log-Cauchy distribution may be an appropriate model is the time between someone becoming infected with HIV virus and showing symptoms of the disease, which may be very long for some people.[3] It has also been proposed as a model for species abundance patterns.[18]
References
- ^ a b c d e f Olive, D.J. (June 23, 2008). "Applied Robust Statistics" (PDF). Southern Illinois University. p. 86. Retrieved 2011-10-18.
- ^ a b Lindsey, J.K. (2004). Statistical analysis of stochastic processes in time. Cambridge University Press. p. 33, 50, 56, 62, 145. ISBN 978-0-521-83741-5.
- ^ a b c d Mode, C.J. & Sleeman, C.K. (2000). Stochastic processes in epidemiology: HIV/AIDS, other infectious diseases. World Scientific. pp. 29–37. ISBN 978-981-02-4097-4.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ a b c d e f Marshall, A.W. & Olkin, I. (2007). Life distributions: structure of nonparametric, semiparametric, and parametric families. Springer. pp. 443–444. ISBN 978-0-387-20333-1.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ a b Falk, M., Hüsler, J. & Reiss, R. (2010). "Laws of Small Numbers: Extremes and Rare Events". Springer. p. 80. ISBN 978-3-0348-0008-2.
{{cite web}}: Missing or empty|url=(help)CS1 maint: multiple names: authors list (link) - ^ Alves, M.I.F., de Haan, L. & Neves, C. (March 10, 2006). "Statistical inference for heavy and super-heavy tailed distributions" (PDF).
{{cite web}}: CS1 maint: multiple names: authors list (link) - ^ "Moment". Mathworld. Retrieved 2011-10-19.
- ^ Wang, Y. "Trade, Human Capital and Technology Spillovers: An Industry Level Analysis". Carleton University. p. 14.
{{cite web}}:|access-date=requires|url=(help); Missing or empty|url=(help) - ^ Bondesson, L. (2003). "On the Levy Measure of the Lognormal and LogCauchy Distributions". Methodology and Computing in Applied Probability. Kluwer Academic Publications. pp. 243–256. Retrieved 2011-10-18.
- ^ Knight, J. & Satchell, S. (2001). Return distributions in finance. Butterworth-Heinemann. p. 153. ISBN 978-0-7506-4751-9.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Kemp, M. (2009). Market consistency: model calibration in imperfect markets. Wiley. ISBN 978-0-470-77088-7.
- ^ MacDonald, J.B. (1981). "Measuring Income Inequality". In Taillie, C., Patil, G.P. & Baldessari, B. (ed.). Statistical distributions in scientific work: proceedings of the NATO Advanced Study Institute. Springer. p. 169. ISBN 978-90-277-1334-6.
{{cite book}}: CS1 maint: multiple names: editors list (link) - ^ a b Kleiber, C. & Kotz, S. (2003). Statistical Size Distributions in Economics and Actuarial Science. Wiley. pp. 101–102, 110. ISBN 978-0-471-15064-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Panton, D.B. (May 1993). "Distribution function values for logstable distributions". Computers & Mathematics with Applications. 25 (9): 17–24. doi:10.1016/0898-1221(93)90128-I. Retrieved 2011-10-18.
- ^ Good, I.J. (1983). Good thinking: the foundations of probability and its applications. University of Minnesota Press. p. 102. ISBN 978-0-8166-1142-3.
- ^ Chen, M. (2010). Frontiers of Statistical Decision Making and Bayesian Analysis. Springer. p. 12. ISBN 978-1-4419-6943-9.
- ^ Lindsey, J.K., Jones, B. & Jarvis, P. (September 2001). "Some statistical issues in modelling pharmacokinetic data". Statistics in Medicine. 20 (17–18): 2775–278. doi:10.1002/sim.742. Retrieved 2011-10-19.
{{cite journal}}: Text "10.1002/sim.742" ignored (help)CS1 maint: multiple names: authors list (link) - ^ Zuo-Yun, Y.; et al. (June 2005). "LogCauchy, log-sech and lognormal distributions of species abundances in forest communities". Ecological Modelling. 184 (2–4): 329–340. doi:10.1016/j.ecolmodel.2004.10.011. Retrieved 2011-10-18.
{{cite journal}}: Explicit use of et al. in:|author=(help)




![{\displaystyle {1 \over x\pi }\left[{\sigma \over (\ln x-\mu )^{2}+\sigma ^{2}}\right],\ \ x>0}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/8ac7d87d9737a9d396f445dfeb9b4cff6c3d0a12)


![{\displaystyle {\begin{aligned}f(x;\mu ,\sigma )&={\frac {1}{x\pi \sigma \left[1+\left({\frac {\ln x-\mu }{\sigma }}\right)^{2}\right]}},\ \ x>0\\&={1 \over x\pi }\left[{\sigma \over (\ln x-\mu )^{2}+\sigma ^{2}}\right],\ \ x>0\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/a188fc444184e191f4e0325b64a2fb201546adfe)








