Hexagon

For other uses, see Hexagon (disambiguation).

Template:Even polygon stat table In geometry, a hexagon (from Greek ἕξ hex, "six") is a polygon with six edges and six vertices. A regular hexagon has Schläfli symbol {6}. The total of the internal angles of any hexagon is 720°.

Regular hexagon

A step-by-step animation of the construction of a regular hexagon using compass and straightedge, given by Euclid's Elements, Book IV, Proposition 15.

A regular hexagon has all sides of the same length, and all internal angles are 120 degrees. A regular hexagon has 6 rotational symmetries (rotational symmetry of order six) and 6 reflection symmetries (six lines of symmetry), making up the dihedral group D₆. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle with a vertex at the center of the regular hexagon and sharing one side with the hexagon is equilateral, and that the regular hexagon can be partitioned into six equilateral triangles.

Like squares and equilateral triangles, regular hexagons fit together without any gaps to tile the plane (three hexagons meeting at every vertex), and so are useful for constructing tessellations. The cells of a beehive honeycomb are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram of a regular triangular lattice is the honeycomb tessellation of hexagons. It is not usually considered a triambus, although it is equilateral.

The area of a regular hexagon of side length t is given by

$A={\frac {3{\sqrt {3}}}{2}}t^{2}\simeq 2.598076211t^{2}.$

An alternative formula for area is A = 1.5dt where the length d is the distance between the parallel sides (also referred to as the flat-to-flat distance), or the height of the hexagon when it sits on one side as base, or the diameter of the inscribed circle.

Another alternative formula for the area if only the flat-to-flat distance, d, is known, is given by

$A={\frac {\sqrt {3}}{2}}d^{2}\simeq 0.866025404d^{2}.$

The area can also be found by the formulas $A=ap/2$ and $\scriptstyle A\ =\ {2}a^{2}{\sqrt {3}}\ \simeq \ 3.464102a^{2}$, where a is the apothem and p is the perimeter.

The perimeter of a regular hexagon of side length t is 6t, its maximal diameter 2t, and its minimal diameter $\scriptstyle d\ =\ t{\sqrt {3}}$.

If a regular hexagon has successive vertices A, B, C, D, E, F and if P is any point on the circumscribing circle between B and C, then PE + PF = PA + PB + PC + PD.

Cyclic hexagon

A cyclic hexagon is any hexagon inscribed in a circle. If the successive sides of the cyclic hexagon are a, b, c, d, e, f, then the three main diagonals intersect in a single point if and only if ace = bdf.

Hexagon inscribed in a conic section

Pascal's theorem (also known as the "Hexagrammum Mysticum Theorem") states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the "Pascal line" of that configuration.

Hexagon tangential to a conic section

Let ABCDEF be a hexagon formed by six tangent lines of a conic section. Then Brianchon's theorem states that the three main diagonals AD, BE, and CF intersect at a single point.

In a hexagon that is tangential to a circle and that has consecutive sides a, b, c, d, e, and f,

$a+c+e=b+d+f.$

Related figures

A regular hexagon can also be created as a truncated equilateral triangle, with Schläfli symbol t{3}. This form only has D3 symmetry. In this figure, the remaining edges of the original triangle are drawn blue, and new edges from the truncation are red.

The hexagram can be created as a stellation process: extending the 6 edges of a regular hexagon until they meet at 6 new vertices.

A concave hexagon

A self-intersecting hexagon (star polygon)

A (nonplanar) skew regular hexagon, within the edges of a cube

Petrie polygons

The regular hexagon is the Petrie polygon for these regular and uniform polytopes, shown in these skew orthogonal projections:

(3D)		(5D)
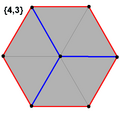Cube	Octahedron	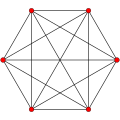5-simplex	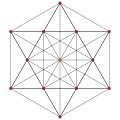Rectified 5-simplex	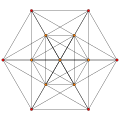Birectified 5-simplex

Polyhedra with hexagons

There is no platonic solid made of only regular hexagons, because the hexagons tessellate, not allowing the result to "fold up". The Archimedean solids with some hexagonal faces are the truncated tetrahedron, truncated octahedron, truncated icosahedron (of soccer ball and fullerene fame), truncated cuboctahedron and the truncated icosidodecahedron.

Archimedean solids
truncated tetrahedron	truncated octahedron	truncated icosahedron	truncated cuboctahedron	truncated icosidodecahedron

There are also 9 Johnson solids:

• triangular cupola, elongated triangular cupola, gyroelongated triangular cupola, augmented hexagonal prism, parabiaugmented hexagonal prism, metabiaugmented hexagonal prism, triaugmented hexagonal prism, augmented truncated tetrahedron, triangular hebesphenorotunda

Prismoids
Hexagonal prism	Hexagonal antiprism	Hexagonal pyramid

Other symmetric polyhedra
Truncated triakis tetrahedron	Truncated rhombic dodecahedron	Truncated rhombic triacontahedron

Regular and uniform tilings with hexagons

The hexagon can form a regular tessellate the plane with a Schläfli symbol {6,3}, having 3 hexagons around every vertex.	A second hexagonal tessellation of the plane can be formed as a truncated triangular tiling or rhombille tiling, with one of three hexagons colored differently.	A third tessellation of the plane can be formed with three colored hexagons around every vertex.
Trihexagonal tiling	Trihexagonal tiling
Rhombitrihexagonal tiling	Truncated trihexagonal tiling

Hexagons: natural and human-made

• 
  Assembled E-ELT mirror segments
• 
  A beehive honeycomb
• 
  The scutes of a turtle's carapace
• 
  North polar hexagonal cloud feature on Saturn, discovered by Voyager 1 and confirmed in 2006 by Cassini [1] [2] [3]
• 
  Micrograph of a snowflake
• 
  Benzene, the simplest aromatic compound with hexagonal shape.
• 
  Crystal structure of a molecular hexagon composed of hexagonal aromatic rings reported by Müllen and coworkers in Chem. Eur. J., 2000, 1834-1839.
• 
  Naturally formed basalt columns from Giant's Causeway in Ireland; large masses must cool slowly to form a polygonal fracture pattern
• 
  An aerial view of Fort Jefferson in Dry Tortugas National Park
• 
  The James Webb Space Telescope mirror is composed of 18 hexagonal segments.
• 
  Metropolitan France has a vaguely hexagonal shape. In French, l'Hexagone refers to the European mainland of France aka the "metropole" as opposed to the overseas territories such as Guadeloupe, Martinique or French Guiana.
• 
  Hexagonal Hanksite crystal, one of many hexagonal crystal system minerals
• 
  Hexagonal barn
• 
  The Hexagon, a hexagonal theatre in Reading, Berkshire

See also

• Hexagram: 6-sided star within a regular hexagon
• Unicursal hexagram: single path, 6-sided star, within a hexagon
• Hexagonal tiling: a regular tiling of hexagons in a plane
• Hexagonal number
• Hexagonal crystal system
• Icositetrachoron: a four-dimensional figure which, like the hexagon, has orthoplex facets and is self-dual

External links

• Weisstein, Eric W. "Hexagon". MathWorld.
• Definition and properties of a hexagon with interactive animation and construction with compass and straightedge.
• Cymatics – Hexagonal shapes occurring within water sound images
• Cassini Images Bizarre Hexagon on Saturn
• Saturn's Strange Hexagon
• A hexagonal feature around Saturn's North Pole
• "Bizarre Hexagon Spotted on Saturn" – from Space.com (27 March 2007)