Elongated dodecahedron: Difference between revisions

Elongated dodecahedron
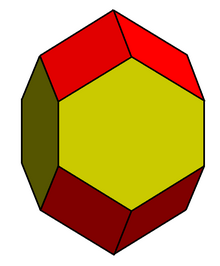
Elongated dodecahedron
Type	Dodecahedron
Faces	8 rhombi; 4 hexagons
Edges	28
Vertices	18
Vertex configuration	(8) 4.6.6; (8) 4.4.6; (2) 4.4.4.4
Symmetry group	D4h, [4,2], (*422), order 16
Rotation group	D4, [4,2]+, (422), order 8
Dual polyhedron	-
Properties	convex, Zonohedron

Browse history interactively

← Previous edit Next edit →

Content deleted Content added

VisualWikitext

Inline

Revision as of 20:05, 5 October 2012

The rhombo-hexagonal dodecahedron is a convex polyhedron with 8 rhombic and 4 equilateral hexagonal faces.

It is also called an elongated dodecahedron and extended rhombic dodecahedron because it is related to the rhombic dodecahedron by expanding four rhombic faces of the rhombic dodecahedron into hexagons.

It can tesselate all space by translations.
It is the Wigner-Seitz cell for certain body-centered tetragonal lattices.

External links

Weisstein, Eric W. "Space-filling polyhedron". MathWorld.
Weisstein, Eric W. "Elongated dodecahedron". MathWorld.
[1] Uniform space-filling using only rhombo-hexagonal dodecahedra
VRML Model [2]

References

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p169

@@ Line 6: / Line 6: @@
   Vertex_Count=18|
   Vertex_List=(8) 4.6.6<BR>(8) 4.4.6<BR>(2) 4.4.4.4|
-  Symmetry_Group=[[Dihedral symmetry in three dimensions|D<sub>4h</sub>]]|
+  Symmetry_Group=[[Dihedral symmetry in three dimensions|D<sub>4h</sub>]], [4,2], (*422), order 16|
+  Rotation_Group=D<sub>4</sub>, [4,2]<sup>+</sup>, (422), order 8|
   Dual=-|
   Property_List=[[convex set|convex]], [[Zonohedron]]