Zernike polynomials

The first 15 Zernike polynomials, ordered vertically by radial degree and horizontally by azimuthal degree.

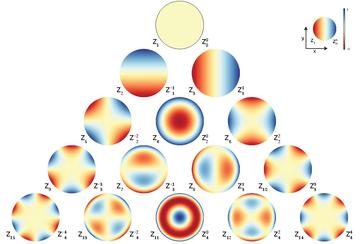
In mathematics, the Zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. Named after Nobel Prize winner and optical physicist, and inventor of the phase contrast microscopy, Frits Zernike, they play an important role in beam optics.

Definitions

There are even and odd Zernike polynomials. The even ones are defined as

$Z_{n}^{m}(\rho ,\varphi )=R_{n}^{m}(\rho )\,\cos(m\,\varphi )\!$

and the odd ones as

$Z_{n}^{-m}(\rho ,\varphi )=R_{n}^{m}(\rho )\,\sin(m\,\varphi ),\!$

where m and n are nonnegative integers with n≥m, φ is the azimuthal angle, and ρ is the radial distance $0\leq \rho \leq 1$. Zernike polynomials have the property of being limited to a range of -1 to +1, i.e. $|Z_{n}^{m}(\rho ,\varphi )|\leq 1$. The radial polynomials R^m_n are defined as

$R_{n}^{m}(\rho )=\!\sum _{k=0}^{(n-m)/2}\!\!\!{\frac {(-1)^{k}\,(n-k)!}{k!\,((n+m)/2-k)!\,((n-m)/2-k)!}}\;\rho ^{n-2\,k}$

for n − m even, and are identically 0 for n − m odd.

Other Representations

Rewriting the ratios of factorials in the radial part as products of binomials shows that the coefficients are integer numbers:

$R_{n}^{m}(\rho )=\sum _{k=0}^{(n-m)/2}(-1)^{k}{\binom {n-k}{k}}{\binom {n-2k}{(n-m)/2-k}}\rho ^{n-2k}$.

A notation as terminating Gaussian Hypergeometric Functions is useful to reveal recurrences, to demonstrate that they are special cases of Jacobi polynomials, to write down the differential equations, etc.:

$R_{n}^{m}(\rho )={\binom {n}{(n+m)/2}}\rho ^{n}{}_{2}F_{1}\left(-{\frac {n+m}{2}},-{\frac {n-m}{2}};-n;\rho ^{-2}\right)$

$=(-1)^{(n+m)/2}{\binom {(n+m)/2}{(n-m)/2}}\rho ^{m}{}_{2}F_{1}\left(1+n,1-{\frac {n-m}{2}};1+{\frac {n+m}{2}};\rho ^{2}\right)$

for n − m even.

Zernike Transform

An arbitrary, real valued, phase-field over a unit disk, $G(\rho ,\varphi )$, can be represented in terms of its Zernike coefficients (odd, and even), just as much as periodic functions find an orthogonal representation with the Fourier series.

$G(\rho ,\varphi )=\sum _{m,n}\left[a_{m,n}Z_{n}^{m}(\rho ,\varphi )+b_{m,n}Z_{n}^{-m}(\rho ,\varphi )\right],$

where the coefficients are calculated by the inner products, $a_{m,n}=<G(\rho ,\varphi ),Z_{n}^{m}(\rho ,\varphi )>,b_{m,n}=<G(\rho ,\varphi ),Z_{n}^{-m}(\rho ,\varphi )>.$ Alternatively we can use the known values of phase function, G, on the circular grid, to form a system of equations. The phase function is retrieved by the unknown coefficient weighted product with (known values) of Zernike polynomial across the unit grid. Hence coefficients can also be found by solving linear system, by matrix-inversion. Fast algorithms to calculate the forward and inverse Zernike transform use symmetry properties of trigonometric functions, separability of radial and azimuthal parts of Zernike polynomials, and their rotational symmetries.

Noll's sequential indices

Applications often involve linear algebra, where integrals over products of Zernike polynomials and some other factor build the matrix elements. To enumerate the rows and columns of these matrices by a single index, a conventional mapping of the two indices n and m to a single index j has been introduced by Noll. The table of this association $Z_{n}^{m}\rightarrow Z_{j}$ starts as follows (sequence A176988 in the OEIS) class="wikitable " The rule is that the even Z (with even azimuthal part m, $\cos(m\varphi )$) obtain even indices j, the odd Z odd indices j. Within a given n, lower values of m obtain lower j.

Properties

Orthogonality

The orthogonality in the radial part reads

$\int _{0}^{1}\rho {\sqrt {2n+2}}R_{n}^{m}(\rho )\,{\sqrt {2n'+2}}R_{n'}^{m}(\rho )d\rho =\delta _{n,n'}$.

Orthogonality in the angular part is represented by

$\int _{0}^{2\pi }\cos(m\varphi )\cos(m'\varphi )d\varphi =\epsilon _{m}\pi \delta _{|m|,|m'|}$,

$\int _{0}^{2\pi }\sin(m\varphi )\sin(m'\varphi )d\varphi =(-1)^{m+m'}\pi \delta _{|m|,|m'|};\quad m\neq 0$,

$\int _{0}^{2\pi }\cos(m\varphi )\sin(m'\varphi )d\varphi =0$,

where $\epsilon _{m}$ (sometimes called the Neumann factor because it frequently appears in conjunction with Bessel functions) is defined as 2 if $m=0$ and 1 if $m\neq 0$. The product of the angular and radial parts establishes the orthogonality of the Zernike functions with respect to both indices if integrated over the unit disk,

$\int Z_{n}^{m}(\rho ,\varphi )Z_{n'}^{m'}(\rho ,\varphi )d^{2}r={\frac {\epsilon _{m}\pi }{2n+2}}\delta _{n,n'}\delta _{m,m'}$,

where $d^{2}r=\rho \,d\rho \,d\varphi$ is the Jacobian of the circular coordinate system, and where $n-m$ and $n'-m'$ are both even.

A special value is

$R_{n}^{m}(1)=1$.

Symmetries

The parity with respect to reflection along the x axis is

$Z_{n}^{m}(\rho ,\varphi )=(-1)^{m}Z_{n}^{m}(\rho ,-\varphi )$.

The parity with respect to point reflection at the center of coordinates is

$Z_{n}^{m}(\rho ,\varphi )=(-1)^{m}Z_{n}^{m}(\rho ,\varphi +\pi )$,

where $(-1)^{m}$ could as well be written $(-1)^{n}$ because $n-m$ is even for the relevant, non-vanishing values. The radial polynomials are also either even or odd, depending on order n or m:

$R_{n}^{m}(\rho )=(-1)^{n}R_{n}^{m}(-\rho )=(-1)^{m}R_{n}^{m}(-\rho )$.

The periodicity of the trigonometric functions implies invariance if rotated by multiples of $2\pi /m$ radian around the center:

$Z_{n}^{m}(\rho ,\varphi +2\pi k/m)=Z_{n}^{m}(\rho ,\varphi ),\quad k=0,\pm 1,\pm 2,\ldots$.

Examples

Radial polynomials

The first few radial polynomials are:

$R_{0}^{0}(\rho )=1\,$

$R_{1}^{1}(\rho )=\rho \,$

$R_{2}^{0}(\rho )=2\rho ^{2}-1\,$

$R_{2}^{2}(\rho )=\rho ^{2}\,$

$R_{3}^{1}(\rho )=3\rho ^{3}-2\rho \,$

$R_{3}^{3}(\rho )=\rho ^{3}\,$

$R_{4}^{0}(\rho )=6\rho ^{4}-6\rho ^{2}+1\,$

$R_{4}^{2}(\rho )=4\rho ^{4}-3\rho ^{2}\,$

$R_{4}^{4}(\rho )=\rho ^{4}\,$

$R_{5}^{1}(\rho )=10\rho ^{5}-12\rho ^{3}+3\rho \,$

$R_{5}^{3}(\rho )=5\rho ^{5}-4\rho ^{3}\,$

$R_{5}^{5}(\rho )=\rho ^{5}\,$

$R_{6}^{0}(\rho )=20\rho ^{6}-30\rho ^{4}+12\rho ^{2}-1\,$

$R_{6}^{2}(\rho )=15\rho ^{6}-20\rho ^{4}+6\rho ^{2}\,$

$R_{6}^{4}(\rho )=6\rho ^{6}-5\rho ^{4}\,$

$R_{6}^{6}(\rho )=\rho ^{6}.\,$

Zernike polynomials

The first few Zernike modes, ordered by Noll index $j$ are

Noll index ($j$)	Radial degree ($n$)	Azimuthal degree ($m$)	$Z_{j}$	Classical name
1	0	0	$1$	Piston
2	1	1	$2\rho \cos \theta$	Tip (lateral position)
3	1	-1	$2\rho \sin \theta$	Tilt (lateral position)
4	2	0	${\sqrt {3}}(2\rho ^{2}-1)$	Defocus (longitudinal position)
5	2	-2	${\sqrt {6}}\rho ^{2}\sin 2\theta$	Astigmatism
6	2	2	${\sqrt {6}}\rho ^{2}\cos 2\theta$	Astigmatism
7	3	-1	${\sqrt {8}}(3\rho ^{3}-2r)\sin \theta$	Coma
8	3	1	${\sqrt {8}}(3\rho ^{3}-2r)\cos \theta$	Coma
9	3	-3	${\sqrt {8}}\rho ^{3}\sin 3\theta$	Trefoil
10	3	3	${\sqrt {8}}\rho ^{3}\cos 3\theta$	Trefoil
11	4	0	${\sqrt {5}}(6\rho ^{4}-6r^{2}+1)$	Third order spherical
12	4	2	${\sqrt {10}}(4\rho ^{4}-3r^{2})\cos 2\theta$	—
13	4	-2	${\sqrt {10}}(4\rho ^{4}-3r^{2})\sin 2\theta$	—
14	4	4	${\sqrt {10}}\rho ^{4}\cos 4\theta$	—
15	4	-4	${\sqrt {10}}\rho ^{4}\sin 4\theta$	—

Applications

The functions are a basis defined over the circular support area, typically the pupil planes in classical optical imaging at visible and infrared wavelengths through systems of lenses and mirrors of finite diameter. Their advantages are the simple analytical properties inherited from the simplicity of the radial functions and the factorization in radial and azimuthal functions; this leads, for example, to closed form expressions of the two-dimensional Fourier transform in terms of Bessel Functions. Their disadvantage, in particular if high n are involved, is the unequal distribution of nodal lines over the unit disk, which introduces ringing effects near the perimeter $\rho \approx 1$, which often leads attempts to define other orthogonal functions over the circular disk.

In precision optical manufacturing, Zernike polynomials are used to characterize higher-order errors observed in interferometric analyses, in order to achieve desired system performance.

In optometry and ophthalmology Zernike polynomials are used to describe aberrations of the cornea or lens from an ideal spherical shape, which result in refraction errors.

They are commonly used in adaptive optics where they can be used to effectively cancel out atmospheric distortion. Obvious applications for this are IR or visual astronomy and Satellite imagery. For example, one of the Zernike terms (for m = 0, n = 2) is called 'de-focus'. By coupling the output from this term to a control system, an automatic focus can be implemented.

Another application of the Zernike polynomials is found in the Extended Nijboer-Zernike (ENZ) theory of diffraction and aberrations.

Zernike polynomials are widely used as basis functions of image moments. Since Zernike polynomials are orthogonal to each other, Zernike moments can represent properties of an image with no redundancy or overlap of information between the moments. Although Zernike moments are significantly dependent on the scaling and the translation of the object in an ROI, their magnitudes are independent of the rotation angle of the object. Thus, they can be utilized to extract features from images that describe the shape characteristics of an object. For instance, Zernike moments are utilized as shape descriptors to classify benign and malignant breast masses.

Higher Dimensions

The concept translates to higher dimensions $D$ if multinomials $x_{1}^{i}x_{2}^{j}\cdots x_{D}^{k}$ in Cartesian coordinates are converted to hyperspherical coordinates, $\rho ^{s}$, $s\leq D$, multiplied by a product of Jacobi Polynomials of the angular variables. In $D=3$ dimensions, the angular variables are Spherical harmonics, for example. Linear combinations of the powers $\rho ^{s}$ define an orthogonal basis $R_{n}^{(l)}(\rho )$ satisfying

$\int _{0}^{1}\rho ^{D-1}R_{n}^{(l)}(\rho )R_{n'}^{(l)}(\rho )d\rho =\delta _{n,n'}$.

(Note that a factor ${\sqrt {2n+D}}$ is absorbed in the definition of $R$ here, whereas in $D=2$ the normalization is chosen slightly differently. This is largely a matter of taste, depending on whether one wishes to maintain an integer set of coefficients or prefers tighter formulas if the orthogonalization is involved.) The explicit representation is

$R_{n}^{(l)}(\rho )={\sqrt {2n+D}}\sum _{s=0}^{(n-l)/2}(-1)^{s}{(n-l)/2 \choose s}{n-s-1+D/2 \choose (n-l)/2}\rho ^{n-2s}$

$=(-1)^{(n-l)/2}{\sqrt {2n+D}}\sum _{s=0}^{(n-l)/2}(-1)^{s}{(n-l)/2 \choose s}{s-1+(n+l+D)/2 \choose (n-l)/2}\rho ^{2s+l}$

$=(-1)^{(n-l)/2}{\sqrt {2n+D}}{(D+n+l)/2-1 \choose (n-l)/2}\rho ^{l}{}_{2}F_{1}(-(n-l)/2,(n+l+D)/2;l+D/2;\rho ^{2})$

for even $n-l\geq 0$, else identical to zero.

See also

• Jacobi polynomials
• Nijboer-Zernike theory
• Pseudo-Zernike polynomials

References

• Weisstein, Eric W. "Zernike Polynomial". MathWorld.
• Callahan, P. G.; De Graef, M. (2012). "Precipitate shape fitting and reconstruction by means of 3D Zernike functions". Model. Simul. Mat. Sci. Engin. 20: 015003. Bibcode:2012MSMSE..20a5003C. doi:10.1088/0965-0393/20/1/015003.
• Campbell, C. E. (2003). "Matrix method to find a new set of Zernike coefficients form an original set when the aperture radius is changed". J. Opt. Soc. Am. A. 20 (2): 209. Bibcode:2003JOSAA..20..209C. doi:10.1364/JOSAA.20.000209.
• Cerjan, C. (2007). "The Zernike-Bessel representation and its application to Hankel transforms". J. Opt. Soc. Am. A. 24 (6): 1609. Bibcode:2007JOSAA..24.1609C. doi:10.1364/JOSAA.24.001609.
• Comastri, S. A.; Perez, L. I.; Perez, G. D.; Martin, G.; Bastida Cerjan, K. (2007). "Zernike expansion coefficients: rescaling and decentering for different pupils and evaluation of corneal aberrations". J. Opt. A: Pure Appl. Opt. 9 (3): 209. Bibcode:2007JOptA...9..209C. doi:10.1088/1464-4258/9/3/001.
• Conforti, G. (1983). "Zernike aberration coefficients from Seidel and higher-order power-series coefficients". Opt. Lett. 8 (7): 407–408. Bibcode:1983OptL....8..407C. doi:10.1364/OL.8.000407.
• Dai, G-m.; Mahajan, V. N. (2007). "Zernike annular polynomials and atmospheric turbulence". J. Opt. Soc. Am. A. 24: 139. Bibcode:2007JOSAA..24..139D. doi:10.1364/JOSAA.24.000139.
• Dai, G-m. (2006). "Scaling Zernike expansion coefficients to smaller pupil sizes: a simpler formula". J. Opt. Soc. Am. A. 23 (3): 539. Bibcode:2006JOSAA..23..539D. doi:10.1364/JOSAA.23.000539.
• Díaz, J. A.; Fernández-Dorado, J.; Pizarro, C.; Arasa, J. (2009). "Zernike Coefficients for Concentric, Circular, Scaled Pupils: An Equivalent Expression". Journal of Modern Optics. 56 (1): 149–155. Bibcode:2009JMOp...56..149D. doi:10.1080/09500340802531224.
• Díaz, J. A.; Fernández-Dorado, J. "Zernike Coefficients for Concentric, Circular, Scaled Pupils". from The Wolfram Demonstrations Project.
• Gu, J.; Shu, H. Z.; Toumoulin, C.; Luo, L. M. (2002). "A novel algorithm for fast computation of Zernike moments". Pattern Recogn. 35 (12): 2905–2911. doi:10.1016/S0031-3203(01)00194-7.
• Herrmann, J. (1981). "Cross coupling and aliasing in modal wave-front estimation". J. Opt. Soc. Am. 71 (8): 989. Bibcode:1981JOSA...71..989H. doi:10.1364/JOSA.71.000989.
• Hu, P. H.; Stone, J.; Stanley, T. (1989). "Application of Zernike polynomials to atmospheric propagation problems". J. Opt. Soc. Am. A. 6 (10): 1595. Bibcode:1989JOSAA...6.1595H. doi:10.1364/JOSAA.6.001595.
• Kintner, E. C. (1976). "On the mathematical properties of the Zernike Polynomials". Opt. Acta. 23 (8): 679. Bibcode:1976AcOpt..23..679K. doi:10.1080/713819334.
• Lawrence, G. N.; Chow, W. W. (1984). "Wave-front tomography by Zernike Polynomial decomposition". Opt. Lett. 9 (7): 267. Bibcode:1984OptL....9..267L. doi:10.1364/OL.9.000267.
• Liu, Haiguang; Morris, Richard J.; Hexemer, A.; Grandison, Scott; Zwart, Peter H. (2012). "Computation of small-angle scattering profiles with three-dimensional Zernike polynomials". Acta Cryst. A (A69): 278–285. doi:10.1107/S010876731104788X.
• Lundström, L.; Unsbo, P. (2007). "Transformation of Zernike coefficients: scaled, translated and rotated wavefronts with circular and elliptical pupils". J. Opt. Soc. Am. A. 24 (3): 569. Bibcode:2007JOSAA..24..569L. doi:10.1364/JOSAA.24.000569.
• Mahajan, V. N. (1981). "Zernike annular polynomials for imaging systems with annular pupils". J. Opt. Soc. Am. 71: 75. Bibcode:1981JOSA...71...75M. doi:10.1364/JOSA.71.000075.
• Mathar, R. J. (2007). "Third Order Newton's Method for Zernike Polynomial Zeros". arXiv:0705.1329 [math.NA]. {{cite arXiv}}: Unknown parameter |bibcode= ignored (help)
• Mathar, R. J. (2009). "Zernike Basis to Cartesian Transformations". Serbian Astronomical Journal. 179 (179): 107–120. arXiv:0809.2368. Bibcode:2009SerAj.179..107M. doi:10.2298/SAJ0979107M.
• Prata Jr, A.; Rusch, W. V. T. (1989). "Algorithm for computation of Zernike polynomials expansion coefficients". Appl. Opt. 28 (4): 749. Bibcode:1989ApOpt..28..749P. doi:10.1364/AO.28.000749.
• Schwiegerling, J. (2002). "Scaling Zernike expansion coefficients to different pupil sizes". J. Opt. Soc. Am. A. 19 (10): 1937. Bibcode:2002JOSAA..19.1937S. doi:10.1364/JOSAA.19.001937.
• Sheppard, C. J. R.; Campbell, S.; Hirschhorn, M. D. (2004). "Zernike expansion of separable functions in Cartesian coordinates". Appl. Opt. 43 (20): 3963. Bibcode:2004ApOpt..43.3963S. doi:10.1364/AO.43.003963.
• Shu, H.; Luo, L.; Han, G.; Coatrieux, J.-L. (2006). "General method to derive the relationship between two sets of Zernike coefficients corresponding to different aperture sizes". J. Opt. Soc. Am. A. 23 (8): 1960. Bibcode:2006JOSAA..23.1960S. doi:10.1364/JOSAA.23.001960.
• Swantner, W.; Chow, W. W. (1994). "Gram-Schmidt orthogonalization of Zernike polynomials for general aperture shapes". Appl. Opt. 33 (10): 1832. Bibcode:1994ApOpt..33.1832S. doi:10.1364/AO.33.001832.
• Tango, W. J. (1977). "The circle polynomials of Zernike and their application in optics". Appl. Phys. A. 13 (4): 327. Bibcode:1977ApPhy..13..327T. doi:10.1007/BF00882606.
• Tyson, R. K. (1982). "Conversion of Zernike aberration coefficients to Seidel and higher-order power series aberration coefficients". Opt. Lett. 7 (6): 262. Bibcode:1982OptL....7..262T. doi:10.1364/OL.7.000262.
• Wang, J. Y.; Silva, D. E. (1980). "Wave-front interpretation with Zernike Polynomials". Appl. Opt. 19 (9): 1510. Bibcode:1980ApOpt..19.1510W. doi:10.1364/AO.19.001510.
• Barakat, R. (1980). "Optimum balanced wave-front aberrations for radially symmetric amplitude distributions: Generalizations of Zernike polynomials". J. Opt. Soc. Am. 70 (6): 739. Bibcode:1980JOSA...70..739B. doi:10.1364/JOSA.70.000739.
• Bhatia, A. B.; Wolf, E. (1952). "The Zernike circle polynomials occurring in diffraction theory". Proc. Phys. Soc. B. 65 (11): 909. Bibcode:1952PPSB...65..909B. doi:10.1088/0370-1301/65/11/112.
• ten Brummelaar, T. A. (1996). "Modeling atmospheric wave aberrations and astronomical instrumentation using the polynomials of Zernike". Opt. Commun. 132 (3–4): 329. Bibcode:1996OptCo.132..329T. doi:10.1016/0030-4018(96)00407-5.
• Novotni, M.; Klein, R. (2003). "3D Zernike Descriptors for Content Based Shape Retrieval" (PDF). Proceedings of the 8th ACM Symposium on Solid Modeling and Applications: 216–225. doi:10.1145/781606.781639.
• Novotni, M.; Klein, R. (2004). "Shape retrieval using 3D Zernike descriptors" (PDF). Computer Aided Design. 36 (11): 1047–1062. doi:10.1016/j.cad.2004.01.005.

External links

• The Extended Nijboer-Zernike website.
• MATLAB code for fast calculation of Zernike moments
• Python/NumPy library for calculating Zernike polynomials
• Zernike aberrations at Telescope Optics
• Example: using WolframAlpha to plot Zernike Polynomials