Shannon–Fano–Elias coding: Difference between revisions
Antares5245 (talk | contribs) No edit summary |
Antares5245 (talk | contribs) No edit summary |
||
| Line 17: | Line 17: | ||
Algorithm: |
Algorithm: |
||
For each ''x'' in ''X'', |
:For each ''x'' in ''X'', |
||
:Let ''Z'' be the binary expansion of <math>F(x)</math>. |
::Let ''Z'' be the binary expansion of <math>F(x)</math>. |
||
:Choose the length of the encoding of ''x'', <math>L(x)</math>, to be the integer<math>\lceil log_2 \frac 1 p(x) \rceil + 1</math> |
::Choose the length of the encoding of ''x'', <math>L(x)</math>, to be the integer <math>\lceil log_2 \frac 1 p(x) \rceil + 1</math> |
||
:Choose the encoding of ''x'', <math>code(x)</math>, be the first <math>L(x)</math> [[Most_significant_bit|most significant bits]] after the decimal point of ''Z''. |
::Choose the encoding of ''x'', <math>code(x)</math>, be the first <math>L(x)</math> [[Most_significant_bit|most significant bits]] after the decimal point of ''Z''. |
||
=== Example === |
=== Example === |
||
| Line 49: | Line 49: | ||
::code(D) is 111 |
::code(D) is 111 |
||
==Algorithm Analysis== |
|||
===Prefix Code=== |
|||
Shannon-Fano-Elias coding produces a binary [[prefix code]], allowing for direct decoding. |
|||
Let bcode(x) be the rational number formed by adding a decimal point before a binary code. For example, if code(C)=1010 then bcode(C) = 0.1010. For all x, if no y exists such that |
|||
:<math>bcode(x) \le bcode(y) < bcode(x) + 2^{-L(x)}</math> |
|||
then all the codes form a prefix code. |
|||
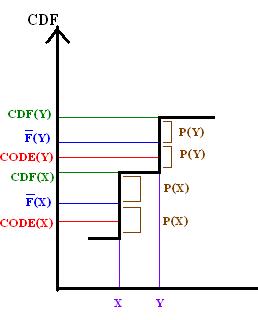
By comparing F to the [[Cumulative_distribution_function|CDF]] of X, this property may be demonstrated graphically for Shannon-Fano-Elias coding. |
|||
[[File:Shannon_fano_elias_cdf_graph.jpg|"CDF"|The relation of F to the CDF of X]] |
|||
By definition of L it follows that |
|||
: <math>2^{-L(x)} \le \frac 12 p(x)</math> |
|||
And because the bits after L(x) are truncated from F(x) to form code(x), it follows that |
|||
: <math>F(x) - bcode(x) \le 2^{-L(x)}</math> |
|||
So the above graph demonstrates the disjoint nature of the ranges for the codes. |
|||
===Entropy=== |
|||
The average code length is |
|||
<math>LC(X) = \sum_{x \epsilon X}p(x)L(x)</math> |
|||
==References== |
==References== |
||
Revision as of 18:03, 24 February 2013
In information theory, Shannon–Fano–Elias coding is a precursor to arithmetic coding, in which probabilities are used to determine codewords.[1]
Algorithm Description
Given a discrete random variable X of ordered values to be encoded, let be the probability for any x in X. Define a function
Algorithm:
- For each x in X,
- Let Z be the binary expansion of .
- Choose the length of the encoding of x, , to be the integer
- Choose the encoding of x, , be the first most significant bits after the decimal point of Z.
Example
Let X = {A, B, C, D}, with probabilities p = {1/3, 1/4, 1/6, 1/4}.
- For A
- Z(A) = = = 0.1666...
- In binary, Z(A) = 0.0010101010...
- L(A) = = 3
- code(A) is 001
- Z(A) = = = 0.1666...
- For B
- Z(B) = = = 0.4583333...
- In binary, Z(B) = 0.01110101010101...
- L(B) = = 3
- code(B) is 011
- Z(B) = = = 0.4583333...
- For C
- Z(C) = = = 0.66666...
- In binary, Z(C) = 0.101010101010...
- L(C) = = 4
- code(C) is 1010
- Z(C) = = = 0.66666...
- For D
- Z(D) = = = 0.875
- In binary, Z(D) = 0.111
- L(D) = = 3
- code(D) is 111
- Z(D) = = = 0.875
Algorithm Analysis
Prefix Code
Shannon-Fano-Elias coding produces a binary prefix code, allowing for direct decoding.
Let bcode(x) be the rational number formed by adding a decimal point before a binary code. For example, if code(C)=1010 then bcode(C) = 0.1010. For all x, if no y exists such that
then all the codes form a prefix code.
By comparing F to the CDF of X, this property may be demonstrated graphically for Shannon-Fano-Elias coding.
By definition of L it follows that
And because the bits after L(x) are truncated from F(x) to form code(x), it follows that
So the above graph demonstrates the disjoint nature of the ranges for the codes.
Entropy
The average code length is
References
- ^ T. M. Cover and Joy A. Thomas (2006). Elements of information theory (2nd ed.). John Wiley and Sons. pp. 127–128. ISBN 978-0-471-24195-9.