Parametric equation

One example of a sketch defined by parametric equations is the butterfly curve.

In mathematics, a parametric equation of a curve is a representation of this curve through equations expressing the coordinates of the points of the curve as functions of a variable called parameter. For example,

${\begin{aligned}x&=\cos t\\y&=\sin t,\end{aligned}}$

is a parametric equation for the unit circle, where t is the parameter.

A common example occurs in kinematics, where the trajectory of a point is usually represented by a parametric equation with the time as parameter.

The notion of parametric equation has been generalized to surfaces and manifolds of higher dimension, with a number of parameters, which is equal to the dimension of the manifold (dimension one and one parameter for curves, dimension two and two parameters for surfaces, etc.).

Parametric equation are pretty useless when is comes to appropriate quadratical functions.

2D examples

Parabola

For example, the simplest equation for a parabola,

$y=x^{2}\,$

can be parametrized by using a free parameter t, and setting

$x=t,y=t^{2}\quad \mathrm {for} -\infty <t<\infty .\,$

Circle

A more sophisticated example might be the following. Consider the unit circle which is described by the ordinary (Cartesian) equation

$x^{2}+y^{2}=1.\,$

This equation can be parametrized as well, giving

$(\cos(t),\sin(t))\quad \mathrm {for} \ 0\leq t<2\pi .\,$

With the Cartesian equation it is easier to check whether a point lies on the circle or not. With the parametric version it is easier to obtain points on a plot.

Several graphs by variation of k

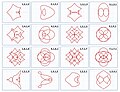
Some sophisticated functions

Other examples are shown:

$x=(a-b)\cos(t)\ +b\cos(t((a/b)-1))$

$y=(a-b)\sin(t)\ -b\sin(t((a/b)-1)),k=a/b$

$x=\cos(at)-\cos(bt)^{j}$

$y=\sin(ct)-\sin(dt)^{k}$

• 
  j=3 k=3
• 
  j=3 k=3
• 
  j=3 k=4
• 
  j=3 k=4
• 
  j=3 k=4

$x=i\cos(at)-\cos(bt)\sin(ct)$

$y=j\sin(dt)-\sin(et)$

• 
  i=1 j=2

3D examples

Helix

Parametric helix

Parametric equations are convenient for describing curves in higher-dimensional spaces. For example:

$x=a\cos(t)\,$

$y=a\sin(t)\,$

$z=bt\,$

describes a three-dimensional curve, the helix, which has a radius of a and rises by 2πb units per turns. Note that the equations are identical in the plane to those for a circle. Such expressions as the one above are commonly written as

$r(t)=(x(t),y(t),z(t))=(a\cos(t),a\sin(t),bt).\,$

Parametric surfaces

A torus with major radius R and minor radius r may be defined parametrically as

$x=\cos(t)(R+r\cos(u)),$

$y=\sin(t)(R+r\cos(u)),$

$z=r\sin(u).$

where the two parameters t and u both vary between 0 and 2π.

• 
  R=2, r=1/2

As u varies from 0 to 2π the point on the surface moves about a short circle passing through the hole in the torus. As t varies from 0 to 2π the point on the surface moves about a long circle around the hole in the torus.

Usefulness

This way of expressing curves is practical as well as efficient; for example, one can integrate and differentiate such curves termwise. Thus, one can describe the velocity of a particle following such a parametrized path as:

$v(t)=r'(t)=(x'(t),y'(t),z'(t))=(-a\sin(t),a\cos(t),b)\,$

and the acceleration as:

$a(t)=r''(t)=(x''(t),y''(t),z''(t))=(-a\cos(t),-a\sin(t),0)\,$

In general, a parametric curve is a function of one independent parameter (usually denoted t). For the corresponding concept with two (or more) independent parameters, see Parametric surface.

Another important use of parametric equations is in the field of computer aided design (CAD). For example, consider the following three representations, all of which are commonly used to describe planar curves.

Type	Form	Example	Description
1. Explicit	$y=f(x)\,\!$	$y=mx+b\,\!$	Line
2. Implicit	$f(x,y)=0\,\!$	$\left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}$	Circle
3. Parametric	$x={\frac {x(t)}{w(t)}}$; $y={\frac {y(t)}{w(t)}}$	$x=a_{0}+a_{1}t;\,\!$ $y=b_{0}+b_{1}t\,\!$ $x=a+r\,\cos t;\,\!$ $y=b+r\,\sin t\,\!$	Line Circle

The first two types are known as analytical or nonparametric representations of curves, and, in general tend to be unsuitable for use in CAD applications. For instance, both are dependent upon the choice of coordinate system and do not lend themselves well to geometric transformations, such as rotations, translations, and scaling. In addition, the implicit representation is awkward for generating points on a curve because x values may be chosen which do not actually lie on the curve. These problems are eliminated by rewriting the equations in parametric form.

Conversion from two parametric equations to a single equation

Converting a set of parametric equations to a single equation involves eliminating the variable $t$ from the simultaneous equations $x=x(t),\ y=y(t)$. If one of these equations can be solved for t, the expression obtained can be substituted into the other equation to obtain an equation involving x and y only. If $x(t)$ and $y(t)$ are rational functions then the techniques of the theory of equations such as resultants can be used to eliminate t. In some cases there is no single equation in closed form that is equivalent to the parametric equations.

To take the example of the circle of radius a above, the parametric equations

$x=a\cos(t)\,$

$y=a\sin(t)\,$

can be simply expressed in terms of x and y by way of the Pythagorean trigonometric identity:

$x/a=\cos(t)\,$

$y/a=\sin(t)\,$

$\cos(t)^{2}+\sin(t)^{2}=1\,\!$

$\therefore (x/a)^{2}+(y/a)^{2}=1,$

which is easily identifiable as a type of conic section (in this case, a circle).

See also

• Curve
• Parametric estimating
• Position vector
• Vector-valued function

External links

• Template:Dmoz
• Web application to draw parametric curves on the plane