Elongated dodecahedron: Difference between revisions
No edit summary |
m Tomruen moved page Rhombo-hexagonal dodecahedron to Elongated dodecahedron over redirect: more standard name |
(No difference)
| |
Revision as of 20:32, 7 August 2013
| Elongated dodecahedron | |
|---|---|
 | |
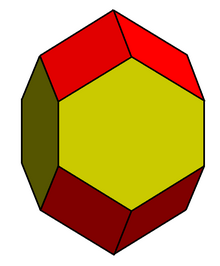| Type | Dodecahedron |
| Faces | 8 rhombi 4 hexagons |
| Edges | 28 |
| Vertices | 18 |
| Vertex configuration | (8) 4.6.6 (8) 4.4.6 (2) 4.4.4.4 |
| Symmetry group | D4h, [4,2], (*422), order 16 |
| Rotation group | D4, [4,2]+, (422), order 8 |
| Dual polyhedron | - |
| Properties | convex, Zonohedron |
In geometry, the elongated dodecahedron, extended rhombic dodecahedron, or rhombo-hexagonal dodecahedron is a convex polyhedron with 8 rhombic and 4 equilateral hexagonal faces. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism.
Tessellation
- It can tesselate all space by translations.
- It is the Wigner-Seitz cell for certain body-centered tetragonal lattices.
This is related to the rhombic dodecahedral honeycomb with an elongation of zero.
External links
- Weisstein, Eric W. "Space-filling polyhedron". MathWorld.
- Weisstein, Eric W. "Elongated dodecahedron". MathWorld.
- [1] Uniform space-filling using only rhombo-hexagonal dodecahedra
- VRML Model [2]
![[1]](http://www.nanomedicine.com/NMI/Figures/5.7.jpg){kind=link}
References
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. rhombo-hexagonal dodecahedron, p169
- H.S.M. Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 p.257