Standard RAID levels

The standard RAID levels are a basic set of RAID configurations that employ the techniques of striping, mirroring, or parity to create large reliable data stores from general purpose computer hard disk drives. The most common types today are RAID 0 (striping), RAID 1 and variants (mirroring), RAID 5 (distributed parity) and RAID 6 (dual parity). RAID levels and their associated data formats are standardized by the Storage Networking Industry Association in the Common RAID Disk Drive Format (DDF) standard.

RAID 0

Diagram of a RAID 0 setup

A RAID 0 (also known as a stripe set or striped volume) splits data evenly across two or more disks (striped) without parity information for speed. RAID 0 was not one of the original RAID levels and provides no data redundancy. RAID 0 is normally used to increase performance, although it can also be used as a way to create a large logical disk out of two or more physical ones.

A RAID 0 can be created with disks of differing sizes, but the storage space added to the array by each disk is limited to the size of the smallest disk. For example, if a 100 GB disk is striped together with a 350 GB disk, the size of the array will be 200 GB (100 GB × 2).

${\begin{aligned}\mathrm {Size} &=2\cdot \min \left(100\,\mathrm {GB} ,350\,\mathrm {GB} \right)\\&=2\cdot 100\,\mathrm {GB} \\&=200\,\mathrm {GB} \end{aligned}}$

The diagram shows how the data is distributed into Ax stripes to the disks. Accessing the stripes in the order A1, A2, A3, ... provides the illusion of a larger and faster drive. Once the stripe size is defined on creation it needs to be maintained at all times.

Performance

RAID 0 is also used in areas where performance is desired and data integrity is not very important, for example in some computer gaming systems. Although some real-world tests with computer games showed a minimal performance gain when using RAID 0, albeit with some desktop applications benefiting, another article examined these claims and concluded: "Striping does not always increase performance (in certain situations it will actually be slower than a non-RAID setup), but in most situations it will yield a significant improvement in performance."

RAID 1

Diagram of a RAID 1 setup

An exact copy (or mirror) of a set of data on two disks. This is useful when read performance or reliability is more important than data storage capacity. Such an array can only be as big as the smallest member disk. A classic RAID 1 mirrored pair contains two disks.

RAID 2

RAID Level 2

A RAID 2 stripes data at the bit (rather than block) level, and uses a Hamming code for error correction. The disks are synchronized by the controller to spin at the same angular orientation (they reach Index at the same time), so it generally cannot service multiple requests simultaneously. Extremely high data transfer rates are possible. This is the only original level of RAID that is not currently used.

All hard disks eventually implemented Hamming code error correction. This made RAID 2 error correction redundant and unnecessarily complex. This level quickly became useless and is now obsolete. There are no commercial applications of RAID 2.

RAID 3

Diagram of a RAID 3 setup of 6-byte blocks and two parity bytes, shown are two blocks of data in different colors.

A RAID 3 uses byte-level striping with a dedicated parity disk. RAID 3 is very rare in practice. One of the characteristics of RAID 3 is that it generally cannot service multiple requests simultaneously. This happens because any single block of data will, by definition, be spread across all members of the set and will reside in the same location. So, any I/O operation requires activity on every disk and usually requires synchronized spindles.

This makes it suitable for applications that demand the highest transfer rates in long sequential reads and writes, for example uncompressed video editing. Applications that make small reads and writes from random disk locations will get the worst performance out of this level.

The requirement that all disks spin synchronously, a.k.a. lockstep, added design considerations to a level that didn't give significant advantages over other RAID levels, so it quickly became useless and is now obsolete. Both RAID 3 and RAID 4 were quickly replaced by RAID 5. RAID 3 was usually implemented in hardware, and the performance issues were addressed by using large disk caches.

RAID 4

Diagram of a RAID 4 setup with dedicated parity disk with each color representing the group of blocks in the respective parity block (a stripe)

A RAID 4 uses block-level striping with a dedicated parity disk.

In the example on the right, a read request for block A1 would be serviced by disk 0. A simultaneous read request for block B1 would have to wait, but a read request for B2 could be serviced concurrently by disk 1.

RAID 4 is very uncommon, but one enterprise level company that has previously used it is NetApp. The aforementioned performance problems were solved with their proprietary Write Anywhere File Layout (WAFL), an approach to writing data to disk locations that minimizes the conventional parity RAID write penalty. By storing system metadata (inodes, block maps, and inode maps) in the same way application data is stored, WAFL is able to write file system metadata blocks anywhere on the disk. This approach in turn allows multiple writes to be "gathered" and scheduled to the same RAID stripe—eliminating the traditional read-modify-write penalty prevalent in parity-based RAID schemes.

RAID 5

Diagram of a RAID 5 setup with distributed parity with each color representing the group of blocks in the respective parity block (a stripe). This diagram shows left asymmetric algorithm

A RAID 5 comprises block-level striping with distributed parity. Unlike in RAID 4, parity information is distributed among the drives. It requires that all drives but one be present to operate. Upon failure of a single drive, subsequent reads can be calculated from the distributed parity such that no data is lost. RAID 5 requires at least three disks.

RAID 6

Diagram of a RAID 6 setup, which is identical to RAID 5 other than the addition of a second parity block

RAID 6 extends RAID 5 by adding an additional parity block; thus it uses block-level striping with two parity blocks distributed across all member disks.

Performance (speed)

RAID 6 does not have a performance penalty for read operations, but it does have a performance penalty on write operations because of the overhead associated with parity calculations. Performance varies greatly depending on how RAID 6 is implemented in the manufacturer's storage architecture – in software, firmware or by using firmware and specialized ASICs for intensive parity calculations. It can be as fast as a RAID-5 system with one fewer drive (same number of data drives).

Implementation

According to the Storage Networking Industry Association (SNIA), the definition of RAID 6 is: "Any form of RAID that can continue to execute read and write requests to all of a RAID array's virtual disks in the presence of any two concurrent disk failures. Several methods, including dual check data computations (parity and Reed-Solomon), orthogonal dual parity check data and diagonal parity, have been used to implement RAID Level 6."

Computing parity

Two different syndromes need to be computed in order to allow the loss of any two drives. One of them, P can be the simple XOR of the data across the stripes, as with RAID 5. A second, independent syndrome is more complicated and requires the assistance of field theory.

To deal with this, the Galois field $GF(m)$ is introduced with $m=2^{k}$, where $GF(m)\cong F_{2}[x]/(p(x))$ for a suitable irreducible polynomial $p(x)$ of degree $k$. A chunk of data can be written as $d_{k-1}d_{k-2}...d_{0}$ in base 2 where each $d_{i}$ is either 0 or 1. This is chosen to correspond with the element $d_{k-1}x^{k-1}+d_{k-2}x^{k-2}+...+d_{1}x+d_{0}$ in the Galois field. Let $D_{0},...,D_{n-1}\in GF(m)$ correspond to the stripes of data across hard drives encoded as field elements in this manner (in practice they would probably be broken into byte-sized chunks). If $g$ is some generator of the field and $\oplus$ denotes addition in the field while concatenation denotes multiplication, then $\mathbf {P}$ and $\mathbf {Q}$ may be computed as follows ($n$ denotes the number of data disks):

$\mathbf {P} =\bigoplus _{i}{D_{i}}=\mathbf {D} _{0}\;\oplus \;\mathbf {D} _{1}\;\oplus \;\mathbf {D} _{2}\;\oplus \;...\;\oplus \;\mathbf {D} _{n-1}$

$\mathbf {Q} =\bigoplus _{i}{g^{i}D_{i}}=g^{0}\mathbf {D} _{0}\;\oplus \;g^{1}\mathbf {D} _{1}\;\oplus \;g^{2}\mathbf {D} _{2}\;\oplus \;...\;\oplus \;g^{n-1}\mathbf {D} _{n-1}$

For a computer scientist, a good way to think about this is that $\oplus$ is a bitwise XOR operator and $g^{i}$ is the action of a linear feedback shift register on a chunk of data. Thus, in the formula above, the calculation of P is just the XOR of each stripe. This is because addition in any characteristic two finite field reduces to the XOR operation. The computation of Q is the XOR of a shifted version of each stripe.

Mathematically, the generator is an element of the field such that $g^{i}$ is different for each nonnegative $i$ satisfying $i<n$.

If one data drive is lost, the data can be recomputed from P just like with RAID 5. If two data drives are lost or a data drive and the drive containing P are lost, the data can be recovered from P and Q or from just Q, respectively, using a more complex process. Working out the details is extremely hard with field theory. Suppose that $D_{i}$ and $D_{j}$ are the lost values with $i\neq j$. Using the other values of $D$, constants $A$ and $B$ may be found so that $D_{i}\oplus D_{j}=A$ and $g^{i}D_{i}\oplus g^{j}D_{j}=B$:

$A=\bigoplus _{\ell :\;\ell \not =i\;\mathrm {and} \;\ell \not =j}{D_{\ell }}=\mathbf {P} \;\oplus \;\mathbf {D} _{0}\;\oplus \;\mathbf {D} _{1}\;\oplus \;\dots \;\oplus \;\mathbf {D} _{i-1}\;\oplus \;\mathbf {D} _{i+1}\;\oplus \;\dots \;\oplus \;\mathbf {D} _{j-1}\;\oplus \;\mathbf {D} _{j+1}\;\oplus \;\dots \;\oplus \;\mathbf {D} _{n-1}$

$B=\bigoplus _{\ell :\;\ell \not =i\;\mathrm {and} \;\ell \not =j}{g^{\ell }D_{\ell }}=\mathbf {Q} \;\oplus \;g^{0}\mathbf {D} _{0}\;\oplus \;g^{1}\mathbf {D} _{1}\;\oplus \;\dots \;\oplus \;g^{i-1}\mathbf {D} _{i-1}\;\oplus \;g^{i+1}\mathbf {D} _{i+1}\;\oplus \;\dots \;\oplus \;g^{j-1}\mathbf {D} _{j-1}\;\oplus \;g^{j+1}\mathbf {D} _{j+1}\;\oplus \;\dots \;\oplus \;g^{n-1}\mathbf {D} _{n-1}$

Multiplying both sides of the equation for $B$ by $g^{n-i}$ and adding to the former equation yields $(g^{n-i+j}\oplus 1)D_{j}=g^{n-i}B\oplus A$ and thus a solution for $D_{j}$, which may be used to compute $D_{i}$.

The computation of Q is CPU intensive compared to the simplicity of P. Thus, a RAID 6 implemented in software will have a more significant effect on system performance, and a hardware solution will be more complex.

Comparison

The following table provides an overview of some considerations for standard RAID levels. In each case:

• Array space efficiency is given as an expression in terms of the number of drives, $n$; this expression designates a fractional value between zero and one, representing the fraction of the sum of the drives' capacities that is available for use. For example, if three drives are arranged in RAID 3, this gives an array space efficiency of $1-(1/n)=1-(1/3)=2/3\approx 67\%$ thus, if each drive in this example has a capacity of 250 GB, then the array has a total capacity of 750 GB but the capacity that is usable for data storage is only 500 GB.
• Array failure rate is given as an expression in terms of the number of drives, $n$, and the drive failure rate, $r$ (which is assumed identical and independent for each drive) and can be seen to be a Bernoulli trial. For example, if each of three drives has a failure rate of 5% over the next three years, and these drives are arranged in RAID 3, then this gives an array failure rate over the next three years of:

${\begin{aligned}1-(1-r)^{n}-nr(1-r)^{n-1}&=1-(1-5\%)^{3}-3\times 5\%\times (1-5\%)^{3-1}\\&=1-0.95^{3}-0.15\times 0.95^{2}\\&=1-0.857375-0.135375\\&=0.00725\\&\approx 0.7\%\end{aligned}}$

Level	Description	Minimum number of drives	Space efficiency	Fault tolerance	Array failure rate	Read performance	Write performance	Figure
RAID 0	Block-level striping without parity or mirroring	2	1	0 (none)	$1-(1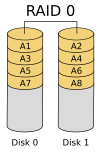-r)^{n}$	n×	n×
RAID 1	Mirroring without parity or striping	2	1/n	n−1 drives	$r^{n}$	n×	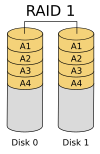1×
RAID 2	Bit-level striping with dedicated Hamming-code parity	3	1 − 1/n ⋅ log2(n-1)	RAID 2 can recover from one drive failure or repair corrupt data or parity when a corrupted bit's corresponding data and parity are good.	(Varies)	(Varies)	(Varies)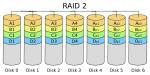
RAID 3	Byte-level striping with dedicated parity	3	1 − 1/n	1 drive	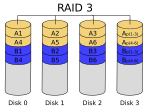$1-(1-r)^{n}-nr(1-r)^{n-1}$	(n−1)×	(n−1)×
RAID 4	Block-level striping with dedicated parity	3	1 − 1/n	1 drive	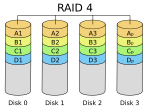$1-(1-r)^{n}-nr(1-r)^{n-1}$	(n−1)×	(n−1)×
RAID 5	Block-level striping with distributed parity	3	1 − 1/n	1 drive	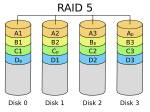$1-(1-r)^{n}-nr(1-r)^{n-1}$	(n−1)×	(n−1)×
RAID 6	Block-level striping with double distributed parity	4	1 − 2/n	2 drives	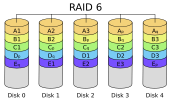$1-(1-r)^{n}-nr(1-r)^{n-1}-{n \choose 2}r^{2}(1-r)^{n-2}$	(n−2)×	(n−2)×
RAID 1+0	Mirroring without parity, and block-level striping	4	2/n	1 drive / span		n×	(n/spans)×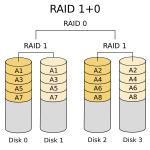
Level	Description	Minimum number of drives	Space efficiency	Fault tolerance	Array failure rate	Read performance	Write performance	Figure

Non-standard RAID levels and non-RAID drive architectures

Main articles: Non-standard RAID levels and Non-RAID drive architectures

Alternatives to the above designs include nested RAID levels, non-standard RAID levels, and non-RAID drive architectures. Non-RAID drive architectures are referred to by similar acronyms, notably SLED, Just a Bunch of Disks, SPAN/BIG, and MAID.

External links

• RAID Calculator for Standard RAID Levels and Other RAID Tools
• IBM summary on RAID levels
• RAID 5 parity explanation and checking tool
• Animations and details on RAID levels 0, 1, and 5
• The Open-E Blog. "How does RAID 5 work? The Shortest and Easiest explanation ever!"