Truncated order-6 square tiling: Difference between revisions
→External links: {{Tessellation}} |
|||
| Line 72: | Line 72: | ||
* [http://geometrygames.org/KaleidoTile/index.html KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings] |
* [http://geometrygames.org/KaleidoTile/index.html KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings] |
||
* [http://www.plunk.org/~hatch/HyperbolicTesselations Hyperbolic Planar Tessellations, Don Hatch] |
* [http://www.plunk.org/~hatch/HyperbolicTesselations Hyperbolic Planar Tessellations, Don Hatch] |
||
{{Tessellation}} |
|||
[[Category:Tessellation]] |
[[Category:Tessellation]] |
||
Revision as of 14:30, 20 October 2014
| Truncated order-6 square tiling | |
|---|---|
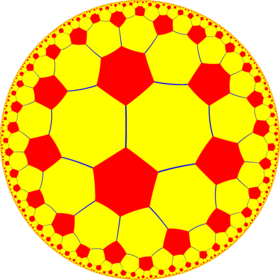 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 8.8.6 |
| Schläfli symbol | t{4,6} |
| Wythoff symbol | 2 6 | 4 |
| Coxeter diagram | |
| Symmetry group | [6,4], (*642) [(3,3,4)], (*334) |
| Dual | Order-4 hexakis hexagonal tiling |
| Properties | Vertex-transitive |
In geometry, the truncated order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{4,6}.
Uniform colorings
Symmetry
The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The symmetry can be doubled as 642 symmetry by adding a mirror bisecting the fundamental domain.
A larger subgroup is constructed [(4,4,3*)], index 6, as (3*22) with gyration points removed, becomes (*222222).
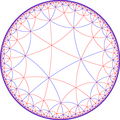 Fundamental domains |

|
 
|
|---|---|---|
| Subgroup index | 1 | 2 |
| Coxeter (orbifold) |
[(4,4,3)] (*443) |
[(4,1+,4,3)] (*3232) |
| [(4,4,3+)] (3*22) | ||
| Rotation subgroups | ||
| Subgroup index | 2 | 4 |
| Coxeter (orbifold) |
[(4,4,3)]+ (443) |
[(4,1+,4,3+)] (3232) |
Related polyhedra and tiling
From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular order-4 hexagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.
| Uniform tetrahexagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,4], (*642) (with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (*3232) index 4 subsymmetry) | |||||||||||
= = = |
= |
= = = |
= |
= = = |
= |
||||||

|

|

|
|

|

|

| |||||
| {6,4} | t{6,4} | r{6,4} | t{4,6} | {4,6} | rr{6,4} | tr{6,4} | |||||
| Uniform duals | |||||||||||

|

|

|

|

|

|

| |||||
| V64 | V4.12.12 | V(4.6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Alternations | |||||||||||
| [1+,6,4] (*443) |
[6+,4] (6*2) |
[6,1+,4] (*3222) |
[6,4+] (4*3) |
[6,4,1+] (*662) |
[(6,4,2+)] (2*32) |
[6,4]+ (642) | |||||
= |
= |
= |
= |
= |
= |
||||||

|

|

|

|

|

|

| |||||
| h{6,4} | s{6,4} | hr{6,4} | s{4,6} | h{4,6} | hrr{6,4} | sr{6,4} | |||||
It can also be generated from the (4 4 3) hyperbolic tilings:
| Uniform (4,4,3) tilings | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,4,3)] (*443) | [(4,4,3)]+ (443) |
[(4,4,3+)] (3*22) |
[(4,1+,4,3)] (*3232) | |||||||

|

|

|

|

|

|

|

|

|

|

|
| h{6,4} t0(4,4,3) |
h2{6,4} t0,1(4,4,3) |
{4,6}1/2 t1(4,4,3) |
h2{6,4} t1,2(4,4,3) |
h{6,4} t2(4,4,3) |
r{6,4}1/2 t0,2(4,4,3) |
t{4,6}1/2 t0,1,2(4,4,3) |
s{4,6}1/2 s(4,4,3) |
hr{4,6}1/2 hr(4,3,4) |
h{4,6}1/2 h(4,3,4) |
q{4,6} h1(4,3,4) |
| Uniform duals | ||||||||||

|

|

|

|
|||||||
| V(3.4)4 | V3.8.4.8 | V(4.4)3 | V3.8.4.8 | V(3.4)4 | V4.6.4.6 | V6.8.8 | V3.3.3.4.3.4 | V(4.4.3)2 | V66 | V4.3.4.6.6 |
| *n42 symmetry mutation of truncated tilings: n.8.8 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracompact | |||||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | ||||
| Truncated figures |

|

|

|

|

|

|

|

| |||
| Config. | 2.8.8 | 3.8.8 | 4.8.8 | 5.8.8 | 6.8.8 | 7.8.8 | 8.8.8 | ∞.8.8 | |||
| n-kis figures |

|

|

|

|

|

|

|

| |||
| Config. | V2.8.8 | V3.8.8 | V4.8.8 | V5.8.8 | V6.8.8 | V7.8.8 | V8.8.8 | V∞.8.8 | |||
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.





