APL syntax and symbols: Difference between revisions

Content deleted Content added

Inline

Revision as of 00:12, 16 January 2015

Template:APLcode The APL programming language is distinctive in being symbolic rather than lexical: its primitives are denoted by symbols, not words. These symbols were originally devised as a mathematical notation. APL programmers often assign informal names when discussing functions and operators (for example, product for ×/) but the core functions and operators provided by the language are denoted by non-textual symbols.

Monadic and dyadic functions

Most symbols denote functions or operators. A monadic function takes as its argument the result of evaluating everything to its right. (Moderated in the usual way by parentheses.) A dyadic function has another argument, the first item of data on its left. Many symbols denote both monadic and dyadic functions, interpreted according to use. For example, ⌊3.2 gives 3, the largest integer not above the argument, and 3⌊2 gives 2, the lower of the two arguments.

Functions and operators

APL uses the term operator in Heaviside’s sense as a moderator of a function and operator (informally, however not strictly APL correct, as something that operates on data, ref. relational operator and operators generally) is sometimes used (albeit APL-definition incorrectly) as interchangeable with function.^[1]^[2]^[3]^[4]^[5] Early definitions of APL symbols were very specific about how symbols were categorized, ref. IBM's 5100 APL Reference Manual, first edition, circa 1975.^[6] For example, the operator reduce is denoted by a forward slash and reduces an array along one axis by interposing its function operand. An example of reduce:

      ×/2 3 4
24

 << Equivalent results in APL >>
 << Reduce operator / used at left

      2×3×4
24

In the above case, the reduce or slash operator moderates the multiply function. The expression ×/ evaluates to a monadic function that reduces an array by multiplication. The above case is simplified, imagine multiplying(adding, subtracting or dividing) more than just a few numbers together. (From a vector, ×/ returns the product of all its elements.)

Syntax rules

There is no precedence hierarchy for functions or operators.

The scope of a function determines its arguments. Functions have long right scope: that is, they take as right arguments everything to their right. A dyadic function has short left scope: it takes as its left arguments the first piece of data to its left. For example,

      1 ÷ 2 ⌊ 3 × 4 - 5
¯0.3333333333
      1 ÷ 2 ⌊ 3 × ¯1
¯0.3333333333
      1 ÷ 2 ⌊ ¯3
¯0.3333333333
      1 ÷ ¯3
¯0.3333333333

An operator may have function or data operands and evaluate to a dyadic or monadic function. Operators have long left scope. An operator takes as its left operand the longest function to its left. For example:

The left operand of the each operator ¨ is the index function. The derived function ⍳¨ ("iota") is used monadically and takes as its right the vector 3 3. The left scope of each is terminated by the reduce operator, denoted by the forward slash. Its left operand is the function expression to its left: the outer product of the equals function. (The syntax and 2-glyph symbol of the outer-product operator are both unhappily anomalous.) The result of ∘.=/ is a monadic function. With a function’s usual long right scope, it takes as its right argument the result of ⍳¨3 3. Thus

      (⍳3)(⍳3)
 1 2 3  1 2 3
      (⍳3)∘.=⍳3
 1 0 0
 0 1 0
 0 0 1
      ⍳¨3 3
 1 2 3  1 2 3
      ∘.=/⍳¨3 3
  1 0 0
  0 1 0
  0 0 1

Some interpreters support the compose operator ∘ and the commute operator ⍨. The former "glues" functions together so that foo∘bar is a function that applies function foo to the result of function bar. Where a dyadic function is moderated by commute and then used monadically, its right argument is taken as its left argument as well. Thus a derived function to return an identity matrix:

      im ← ∘.=⍨∘⍳
      im 3
 1 0 0
 0 1 0
 0 0 1

Monadic functions

Name(s)	Notation	Meaning	Unicode codepoint
Roll	?B	One integer selected randomly from the first B integers	U+003F
Ceiling	⌈B	Least integer greater than or equal to B	U+2308
Floor	⌊B	Greatest integer less than or equal to B	U+230A
Shape, Rho	⍴B	Number of components in each dimension of B	U+2374
Not, Tilde	∼B	Logical: ∼1 is 0, ∼0 is 1	U+223C
Absolute value	∣B	Magnitude of B	U+2223
Index generator, Iota	⍳B	Vector of the first B integers	U+2373
Exponential	⋆B	e to the B power	U+22C6
Negation	−B	Changes sign of B	U+2212
Identity	+B	No change to B	U+002B
Signum	×B	¯1 if B<0; 0 if B=0; 1 if B>0	U+00D7
Reciprocal	÷B	1 divided by B	U+00F7
Ravel, Catenate, Laminate	,B	Reshapes B into a vector	U+002C
Matrix inverse, Monadic Quad Divide	⌹B	Inverse of matrix B	U+2339
Pi times	○B	Multiply by π	U+25CB
Logarithm	⍟B	Natural logarithm of B	U+235F
Reversal	⌽B	Reverse elements of B along last axis	U+233D
Reversal	⊖B	Reverse elements of B along first axis	U+2296
Grade up	⍋B	Indices of B which will arrange B in ascending order	U+234B
Grade down	⍒B	Indices of B which will arrange B in descending order	U+2352
Execute	⍎B	Execute an APL expression	U+234E
Monadic format	⍕B	A character representation of B	U+2355
Monadic transpose	⍉B	Reverse the axes of B	U+2349
Factorial	!B	Product of integers 1 to B	U+0021

Monadic APL Symbols Count(per above table) = 24

Dyadic functions

Name(s)	Notation	Meaning	Unicode codepoint
Add	A+B	Sum of A and B	U+002B
Subtract	A−B	A minus B	U+2212
Multiply	A×B	A multiplied by B	U+00D7
Divide	A÷B	A divided by B	U+00F7
Exponentiation	A⋆B	A raised to the B power	U+22C6
Circle	A○B	Trigonometric functions of B selected by A A=1: sin(B) A=2: cos(B) A=3: tan(B)	U+25CB
Deal	A?B	A distinct integers selected randomly from the first B integers	U+003F
Membership, Epsilon	A∈B	1 for elements of A present in B; 0 where not.	U+2208
Maximum	A⌈B	The greater value of A or B	U+2308
Minimum	A⌊B	The smaller value of A or B	U+230A
Reshape, Dyadic Rho	A⍴B	Array of shape A with data B	U+2374
Take	A↑B	Select the first (or last) A elements of B according to ×A	U+2191
Drop	A↓B	Remove the first (or last) A elements of B according to ×A	U+2193
Decode	A⊥B	Value of a polynomial whose coefficients are B at A	U+22A5
Encode	A⊤B	Base-A representation of the value of B	U+22A4
Residue	A∣B	B modulo A	U+2223
Catenation	A,B	Elements of B appended to the elements of A	U+002C
Expansion	A\B	Insert zeros (or blanks) in B corresponding to zeros in A	U+005C
Compression	A/B	Select elements in B corresponding to ones in A	U+002F
Index of, Dyadic Iota	A⍳B	The location (index) of B in A; 1+⌈/⍳⍴A if not found	U+2373
Matrix divide, Dyadic Quad Divide	A⌹B	Solution to system of linear equations, multiple regression Ax = B	U+2339
Rotation	A⌽B	The elements of B are rotated A positions	U+233D
Rotation	A⊖B	The elements of B are rotated A positions along the first axis	U+2296
Logarithm	A⍟B	Logarithm of B to base A	U+235F
Dyadic format	A⍕B	Format B into a character matrix according to A	U+2355
General transpose	A⍉B	The axes of B are ordered by A	U+2349
Combinations	A!B	Number of combinations of B taken A at a time	U+0021
Less than	A<B	Comparison: 1 if true, 0 if false	U+003C
Less than or equal	A≤B	Comparison: 1 if true, 0 if false	U+2264
Equal	A=B	Comparison: 1 if true, 0 if false	U+003D
Greater than or equal	A≥B	Comparison: 1 if true, 0 if false	U+2265
Greater than	A>B	Comparison: 1 if true, 0 if false	U+003E
Not equal	A≠B	Comparison: 1 if true, 0 if false	U+2260
Or	A∨B	Logic: 0 if A and B are 0; 1 otherwise	U+2228
And	A∧B	Logic: 1 if A and B are 1; 0 otherwise	U+2227
Nor	A⍱B	Logic: 1 if both A and B are 0; otherwise 0	U+2371
Nand	A⍲B	Logic: 0 if both A and B are 1; otherwise 1	U+2372

Dyadic APL Symbols Count(per above table) = 37

Operators and axis indicator

Name	Symbol	Example	Meaning (of example)	Unicode codepoint sequence
Reduce (last axis)	/	+/B	Sum across B	U+002F
Reduce (first axis)	⌿	+⌿B	Sum down B	U+233F
Scan (last axis)	\	+\B	Running sum across B	U+005C
Scan (first axis)	⍀	+⍀B	Running sum down B	U+2340
Inner product	.	A+.×B	Matrix product of A and B	U+002E
Outer product	∘.	A∘.×B	Outer product of A and B	U+2218, U+002E

Operators APL Symbols Count(per above table) = 6

Total APL Symbols Count listed(per tables above = monadic, dyadic, operators) = 67 (or 24+37+6)

Notes: The reduce and scan operators expect a dyadic function on their left, forming a monadic composite function applied to the vector on its right.

The product operator "." expects a dyadic function on both its left and right, forming a dyadic composite function applied to the vectors on its left and right. If the function to the left of the dot is "∘" (signifying null) then the composite function is an outer product, otherwise it is an inner product. An inner product intended for conventional matrix multiplication uses the + and × functions, replacing these with other dyadic functions can result in useful alternative operations.

Some functions can be followed by an axis indicator in (square) brackets, i.e. this appears between a function and an array and should not be confused with array subscripts written after an array. For example, given the ⌽ (reversal) function and a two-dimensional array, the function by default operates along the last axis but this can be changed using an axis indicator:

As a particular case, if the dyadic catenate function is followed by an axis indicator, it can be used to laminate (interpose) two arrays depending on whether the axis indicator is less than or greater than the index origin:

        B←1 2 3 4
        C←5 6 7 8
        B,C
1 2 3 4 5 6 7 8
        B,[0.5]C
1 2 3 4
5 6 7 8
        B,[1.5]C
1 5
2 6
3 7
4 8

Flow control

The user may define custom functions which, like variables, are identified by name rather than by a non-textual symbol. The function header defines whether a custom function is niladic, monadic or dyadic, the local names of the result and parameters, and whether it has any local variables.

Niladic function PI:

        ∇ RESULT←PI
          RESULT←○1
        ∇

Monadic function CIRCLEAREA:

        ∇ AREA←CIRCLEAREA RADIUS
          AREA←PI×RADIUS⋆2
        ∇

Dyadic function SEGMENTAREA, with local variables:

        ∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA
          FRACTION←DEGREES÷360
          CA←CIRCLEAREA RADIUS
          AREA←FRACTION×CA
        ∇

Whether functions with the same identifier but different adicity are distinct is implementation-defined. If allowed, then a function CURVEAREA could be defined twice to replace both monadic CIRCLEAREA and dyadic SEGMENTAREA above, with the monadic or dyadic function being selected by the context in which it was referenced.

Custom dyadic functions may usually be applied to parameters with the same conventions as built-in functions, i.e. arrays should either have the same number of elements or one of them should have a single element which is extended. There are exceptions to this, for example a function to convert pre-decimal UK currency to dollars would expect to take a parameter with precisely three elements representing pounds, shillings and pence.^[7]

Inside a program or a custom function, control may be conditionally transferred to a statement identified by a line number or explicit label; if the target is 0 (zero) this terminates the program or returns to a function's caller. The most common form uses the APL compression function, as in the template (condition)/target which has the effect of evaluating the condition to 0 (false) or 1 (true) and then using that to mask the target (if the condition is false it is ignored, if true it is left alone so control is transferred).

Hence the function SEGMENTAREA may be modified to abort returning zero if the parameters are of different sign:

        ∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA ; SIGN
          FRACTION←DEGREES÷360
          CA←CIRCLEAREA RADIUS
          SIGN←(×DEGREES)≠×RADIUS
          AREA←0
          →SIGN/0
          AREA←FRACTION×CA
        ∇

This works as expected if the parameters are scalars or single-element arrays, but not if they are multiple-element arrays since the condition ends up being based on a single element of the SIGN array: in general, operation is unpredictable since APL defines that computers with vector-processing capabilities should parallelise and may reorder array operations as far as possible. This affects not only explicit application of a custom function to arrays, but also its use anywhere that a dyadic function may reasonably be used such as in generation of a table of results:

        90 180 270 ¯90 ∘.SEGMENTAREA 1 ¯2 4
0 0 0
0 0 0
0 0 0
0 0 0

The correct way to formulate a function is to avoid explicit transfers of control and instead use expressions which evaluate correctly in all conditions:

        ∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA ; SIGN
          FRACTION←DEGREES÷360
          CA←CIRCLEAREA RADIUS
          SIGN←(×DEGREES)≠×RADIUS
          AREA←FRACTION×CA×~SIGN
        ∇

        90 180 270 ¯90 ∘.SEGMENTAREA 1 ¯2 4
0.785398163 0           12.5663706
1.57079633  0           25.1327412
2.35619449  0           37.6991118
0           ¯3.14159265 0

Unfortunately this tends to promote use of excessively-complex "one liners" and a "write-only" style, which has done little to endear APL to influential commentators such as Edsger Dijkstra [1].

Miscellaneous

Name	Symbol	Example	Meaning (of example)	Unicode codepoint
High minus	¯	¯3	Denotes a negative number	U+00AF

APL's "high minus" applies to the single number that follows, while the monadic minus function changes the sign of the entire array to its right.

Most APL implementations support a number of system variables and functions, usually preceded by the ⎕ (quad) character. Particularly important and widely-implemented is the ⎕IO (Index Origin) variable, since while the original IBM APL based its arrays on 1 some newer variants base them on zero:

        X←⍳12
        X
1 2 3 4 5 6 7 8 9 10 11 12
        ⎕IO
1
        X[1]
1
        ⎕IO←0
        X[1]
2

There are user functions for e.g. saving the current workspace and terminating the APL environment, there is very little standardisation of these.

Fonts

The Unicode Basic Multilingual Plane includes the APL symbols in the Miscellaneous Technical block,^[8] which are therefore usually rendered accurately from the larger Unicode fonts installed with most modern operating systems. These fonts are rarely designed by typographers familiar with APL glyphs. So, while accurate, the glyphs may look unfamiliar to APL programmers or be difficult to distinguish from one another.

Some Unicode fonts have been designed to display APL well: APLX Upright, APL385 Unicode, and SimPL.

Before Unicode, APL interpreters were supplied with fonts in which APL characters were mapped to less commonly used positions in the ASCII character sets, usually in the upper 128 codepoints. These mappings (and their national variations) were sometimes unique to each APL vendor's interpreter, which, prior to 1987 (unicode created) made the display of APL programs on the Web, in text files and manuals - frequently problematic.

APL2 Keyboard Functions/Symbols Mapping
Note the APL On/Off Key - topmost-rightmost key, just below. Also note the keyboard had some 55 unique(67 listed per tables above, including comparative symbols but several symbols appear in both monadic and dyadic tables) APL symbol keys(55 APL functions/operators are listed in IBM's 5110 APL Reference Manual), thus with the use of alt, shift and ctrl keys - it would theoretically have allowed a maximum of some 59(keys) *4(with 2-key pressing) *3(with tri-key pressing, e.g. ctrl-alt-del) or some 472 different maximum key combinations, approaching the 512 EBCDIC character max(256 chars times 2 codes for each keys-combination). Again, in theory the keyboard pictured below would have allowed for about 472 different APL symbols/functions to be keyboard-input, actively used. In practice early versions were only using something roughly equivalent to 55 APL special symbols(excluding letters, numbers, punctuation, etc. keys). Thus early APL was then only using about 11%(55/472) of a symbolic language's at-that-time utilization potential, based on keyboard # keys limits, again excluding numbers, letters, punctuation, etc. In another sense keyboard symbols utilization was closer to 100%, highly efficient, since EBCDIC only allowed 256 distinct chars, and ASCII only 128.

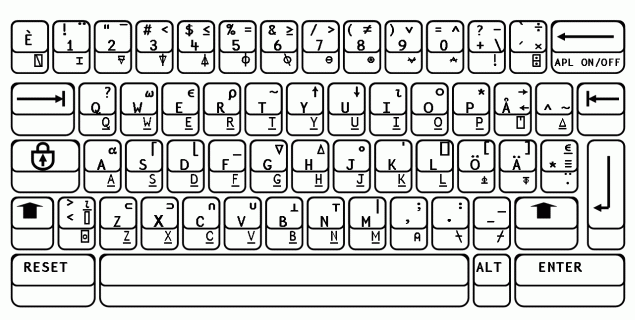
How to Create an APL or Math Symbols Keyboard Layout^[9]
Technical Keys including APL Keys, Unicodes tables and Symbol representations
More modern APL keyboard layout information

References

^ Baronet, Dan. "Sharp APL Operators". http://archive.vector.org.uk. Vector - Journal of the British APL Association. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)
^ MicroAPL. "Primitive Operators". http://www.microapl.co.uk. MicroAPL. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)
^ MicroAPL. "Operators". http://www.microapl.co.uk. MicroAPL. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)
^ Progopedia. "APL". http://progopedia.com. Progopedia. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)
^ Dyalog. "D-functions and operators loosely grouped into categories". http://dfns.dyalog.com. Dyalog. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)
^ IBM. "IBM 5100 APL Reference Manual" (PDF). http://bitsavers.trailing-edge.com. IBM. Retrieved 14 January 2015. {{cite web}}: External link in |website= (help)
^ Berry, Paul "APL\360 Primer Student Text", IBM Research, Thomas J. Watson Research Center, 1969.
^ Unicode chart "Miscellaneous Technical (including APL)" (PDF).
^ Lee, Xah. "How to Create an APL or Math Symbols Keyboard Layout". http://xahlee.info. Xah Lee. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)

External links

APL character reference Page 1
APL character reference Page 2
APL character reference Page 3
APL character reference Page 4
British APL Association fonts page
IBM code page 293 aka the APL code page on mainframes
General information about APL chars on the APL wiki

[1] Baronet, Dan. "Sharp APL Operators". http://archive.vector.org.uk. Vector - Journal of the British APL Association. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)

[2] MicroAPL. "Primitive Operators". http://www.microapl.co.uk. MicroAPL. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)

[3] MicroAPL. "Operators". http://www.microapl.co.uk. MicroAPL. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)

[4] Progopedia. "APL". http://progopedia.com. Progopedia. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)

[5] Dyalog. "D-functions and operators loosely grouped into categories". http://dfns.dyalog.com. Dyalog. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)

[6] IBM. "IBM 5100 APL Reference Manual" (PDF). http://bitsavers.trailing-edge.com. IBM. Retrieved 14 January 2015. {{cite web}}: External link in |website= (help)

[IBM_APL\360_PST_1969-7] Berry, Paul "APL\360 Primer Student Text", IBM Research, Thomas J. Watson Research Center, 1969.

[8] Unicode chart "Miscellaneous Technical (including APL)" (PDF).

[9] Lee, Xah. "How to Create an APL or Math Symbols Keyboard Layout". http://xahlee.info. Xah Lee. Retrieved 13 January 2015. {{cite web}}: External link in |website= (help)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

@@ Line 7: / Line 7: @@
 ==Functions and operators==
 APL uses the term ''operator'' in [[Oliver Heaviside|Heaviside]]’s sense as a moderator of a function and ''operator'' (informally, however ''not'' strictly APL correct, as something that operates on data, ref. [[Relational_operator|relational operator]] and [[Operator_(computer_programming)|operators generally]]) is sometimes used (albeit ''APL-definition'' incorrectly) as interchangeable with  ''function.''<ref>{{cite web|last1=Baronet|first1=Dan|title=Sharp APL Operators|url=http://archive.vector.org.uk/art10000770|website=http://archive.vector.org.uk|publisher=Vector - Journal of the British APL Association|accessdate=13 January 2015}}</ref><ref>{{cite web|last1=MicroAPL|title=Primitive Operators|url=http://www.microapl.co.uk/apl_help/ch_020_010_150.htm|website=http://www.microapl.co.uk|publisher=MicroAPL|accessdate=13 January 2015}}</ref><ref>{{cite web|last1=MicroAPL|title=Operators|url=http://www.microapl.co.uk/apl/apl_concepts_chapter5.html|website=http://www.microapl.co.uk|publisher=MicroAPL|accessdate=13 January 2015}}</ref><ref>{{cite web|last1=Progopedia|title=APL|url=http://progopedia.com/language/apl/|website=http://progopedia.com|publisher=Progopedia|accessdate=13 January 2015}}</ref><ref>{{cite web|last1=Dyalog|title=D-functions and operators loosely grouped into categories|url=http://dfns.dyalog.com/n_contents.htm|website=http://dfns.dyalog.com|publisher=Dyalog|accessdate=13 January 2015}}</ref> Early definitions of APL symbols were very specific about how symbols were categorized, ref. IBM's 5100 APL Reference Manual, first edition, circa 1975.<ref>{{cite web|last1=IBM|title=IBM 5100 APL Reference Manual|url=http://bitsavers.trailing-edge.com/pdf/ibm/5100/SA21-9213-0_IBM_5100aplRef.pdf|website=http://bitsavers.trailing-edge.com|publisher=IBM|accessdate=14 January 2015}}</ref> For example, the operator ''reduce'' is denoted by a forward slash and reduces an array along one axis by interposing its function ''operand''. An example of [[Fold (higher-order function)|reduce]]:
+{{col-begin|width=45%}}
+{{col-break|width=20%}}
 <pre>
       ×/2 3 4
 </pre>
+{{col-break|width=40%}}
-is equivalent to
+  << ''Equivalent results in APL'' >><br> << '''Reduce''' operator '''/''' used at left
+{{col-break|width=20%}}
 <pre>
 ×3×4
 </pre>
+{{col-end}}
-In this case, the ''reduce'' operator moderates the ''multiply'' function. The expression {{unicode|×/}} evaluates to a monadic function that reduces an array by multiplication. (From a vector, it returns the product of its elements.)
+In the above case, the '''reduce''' or '''slash''' operator ''moderates'' the ''multiply'' function. The expression '''{{unicode|×/}}''' evaluates to a monadic function that reduces an array by multiplication.  The above case is simplified, imagine multiplying(adding, subtracting or dividing) more than just a few numbers together. (From a vector, '''{{unicode|×/}}''' returns the product of all its elements.)
 ==Syntax rules==